![Tab := 1/2*a[0]+sum(a[k]*cos(Pi*k*t/T)+b[k]*sin(Pi*k*t/T),k = 1 .. n)](fourier/fourier_101.gif)
Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 3.1.3 bis 3.1.4
Worksheet fourier_10.mws
| > |
c International Thomson Publishing Bonn 1995 filename: fourier.ms
Autor: Komma Datum: 12.8.94
Thema: Harmonische Analyse und Fouriertransformation
| > | restart;with(plots):opt2d:=NULL:opt3d:=NULL: |
Fouriertransformation.
Aufstellen der Fourierreihe mit reellen Koeffizienten (zwei Möglichkeiten a) und b)).
a)
| > | Tab:=a[0]/2+sum(a[k]*cos(Pi*k*t/T)+b[k]*sin(Pi*k*t/T),k=1..n); |
![Tab := 1/2*a[0]+sum(a[k]*cos(Pi*k*t/T)+b[k]*sin(Pi*k*t/T),k = 1 .. n)](fourier/fourier_101.gif)
b)
| > | TA:=a[0]/2+sum(A[k]*sin(Pi*k*t/T+phi[k]),k=1..n); |
![TA := 1/2*a[0]+sum(A[k]*sin(Pi*k*t/T+phi[k]),k = 1 .. n)](fourier/fourier_102.gif)
Impulsfunktion mit Heaviside
| > | imp:=(t0,t1)->Heaviside(t-t0)-Heaviside(t-t1); |
![]()
| > | plot(imp(2,5),t=0..10); |
![[Maple Plot]](fourier/fourier_104.gif)
Stückweise definierte Funktionen mit Heaviside und nicht mit if (boolean-error).
Verschiedene Funktionen zur Auswahl: Gerade, ungerade, gemischt.
Am besten immer mit der Impulsfunktion kombinieren. Härtetest sind auch hier wieder reine sincos-Fktn.
| > | #f:=t->t+t^2; |
| > | #f:=t->t^2; |
| > | #f:=t->t; |
| > | f:=t->t*imp(0,1)+(2-t)*imp(1,2); |
![]()
| > | #f:=t->imp(0,1); |
| > | #f:=t->sin(t)+cos(t); |
Berechnung der Fourierkoeffizienten.
T ist halbe Periodendauer (längere Rechenzeiten zu erwarten)
| > | n:=10: T:=2: # fuer grosses T auch grosses n (>2*T) sonst Harmonische |
| > | for i from 0 to n do |
| > | a[i]:=1/T*evalf(int(f(t)*cos(Pi*i*t/T),t=-T..T)); # evalf fuer Heaviside |
| > | b[i]:=1/T*evalf(int(f(t)*sin(Pi*i*t/T),t=-T..T)); |
| > | A[i]:=sqrt(a[i]^2+b[i]^2); |
| > | phi[i]:=arctan(a[i],b[i]); |
| > | od: |
| > |
| > | #A(); |
| > | #eval(TA,n=3); |
| > |
Annäherung der ausgewählten Funktion als Animation.
| > | n:='n': |
| > | #animate(TA,t=0..3*T,n=1..10); |
| > | display([seq(plot([TA,f(t)],t=0..3*T),n=1..10)],insequence=true); |
![[Maple Plot]](fourier/fourier_106.gif)
| > |
| > |
| > |
| > | #plot(f(t),t=0..3*T); |
Kontrollausgaben, falls gewünscht.
| > | #a(); b();A(); |
| > | #'Tab'=Tab;'TA'=TA; |
Gemeinsame Darstellung von Funktion und zugeordneter Fourierreihe, sowie der Differenz
| > | n:=5: # muss <= als das oben gewaehlte n sein |
| > | plot({f(t),TA},t=0..3*T); |
![[Maple Plot]](fourier/fourier_107.gif)
Grenzen in 10-er Potenzen, falls Sie es auf die Spitze treiben wollen.
| > | plot(f(t)-TA,t=0..3*T,-10^(-1)..10^(-1)); |
![[Maple Plot]](fourier/fourier_108.gif)
Spektrum mit dem histogram-Befehl:
| > | with(stats[statplots]): |
| > | n:=10 : # <= n-original |
| > | histogram([seq(Weight(i,A[i]),i=1..n)],numbars=n,area=count); # braucht evalf, wenn das nicht schon eingesetzt wurde |
![[Maple Plot]](fourier/fourier_109.gif)
| > | #seq(Weight(i,A[i]),i=1..n); |
| > |
Ein diskretes Spektrum bedeutet immer eine periodische Funktion. Man kann zwar die Periodendauer vergrößern (und entsprechend auch die Anzahl der berechneten Harmonischen -- die Summation bis Unendlich ist auch mit Maple nicht zu realisieren) : nach Ablauf einer Periode kommt die Wiederholung. Es sei denn ... man macht T=oo. Nach einer unendlich langen Zeit sollte keine Wiederholung mehr möglich sein!?
D.h. der Grenzübergang (siehe z.B. Jackson) führt zum Fourierintegral oder der Fouriertransformierten, die mit <fourier(f(t),t,w) (nach readlib(fourier)) aufgerufen wird.
| > |
| > | restart; # ist notwendig, weil sonst evalc(abs(x)) nicht funktioniert (nach with(stats)), Maple-Bug (Stand:Jan.95) |
| > |
| > | with(inttrans): |
| > |
| > |
| > | imp:=(t0,t1)->Heaviside(t-t0)-Heaviside(t-t1); |
![]()
Impulsfunktion der Breite tau
| > | f:=t->imp(0,tau); |
![]()
Fourietransformierte
| > | F:=evalc(fourier(f(t),t,w)); |
![]()
Standardtest
| > | tau:=1: |
| > | plot(f(t),t=-1..3); |
![[Maple Plot]](fourier/fourier_1013.gif)
| > | plot({Re(F),Re(F)^2},w=-15..15); |
![[Maple Plot]](fourier/fourier_1014.gif)
Verschiedene Breiten der Impulsfunktion
| > |
| > | plot({seq(evalc(Re(F)),tau=1..3)},w=-15..15); |
![[Maple Plot]](fourier/fourier_1015.gif)
Probe
| > |
| > | tau:='tau': |
Verschiedene Varianten...
| > | invfourier(F,w,t); |
| > |

| > | invfourier('F',w,t); |
![]()
| > | tau:=4: |
| > | invfourier(F,w,t); |
![]()
| > | tau:='tau': |
| > | invfourier(F,w,t) assuming(tau>0); |
![]()
| > |
| > |
Untersuchung eines Frequenzbandes
| > | w1:='w1': w2:='w2': |
| > | impw:=(w1,w2)->Heaviside(w-w1)-Heaviside(w-w2); |
![]()
| > | #impw:=(w1,w2)->Dirac(w-w1)+Dirac(w-w2); |
| > | F:=impw(w1,w2); |
![]()
| > | f:=invfourier(F,w,t); |

| > | #simplify(f); |
| > | evalc(f); |

| > |
In der Rücktransformierten treten nur die Randfrequenzen des Frequenzbandes auf! Insbes. ergibt sich für w1=0 eine mit 1/t variierende Schwingung mit der Frequenz w2. (Vgl. Propagator!)
"Auf einem Frequenz*band* senden" impliziert also einen "Beginn" und ein "Ende" der Sendung (deren Amplitude mit 1/t zu- und abnimmt). Ein *kontinuierliches* Spektrum kann nicht mit konstanter Amplitude abgestrahlt werden. Nur reine Frequenzen -- diskrete -- sind zeitlos, periodisch. Die geringste Unschärfe bedeutet Vergehen, aber auch Entstehen. Idealisten wählen deshalb statt der Heaviside-Funktion die Dirac-Funktion. Oder verhält es sich umgekehrt: ein Sender sendet schon seit einer Milliarde Jahren mit der gleichen Amplitude. Dann kann sein Spektrum nur diskret sein? Oder *gibt* es diesen Sender nicht? Oder liegt der "Beginn" der Sendung schon so lange zurück, daß sich die Amplitude in Menschenzeiten nicht mehr ändert? Vielleicht finden *Sie* die Antwort mit Maple, wenn Sie mit w1, w2 und dem Zeitbereich spielen.
vtitle:=Schwingung_real:vxlab:=Zeit:
| > | w1:=2:w2:=10: |
| > | #w1:=1: w2:=1.000001: # ideal |
pspl(`pfour4.ps`):
| > | plot(evalc(Re(f)),t=2..15); |
![[Maple Plot]](fourier/fourier_1024.gif)
| > | #plot(F(w),w=0..20); |
| > |
Ein weiteres Standardthema: Gauß-Verteilung als Einhüllende einer Cosinus-Schwingung
| > | a:='a': |
| > | F:=simplify(fourier(exp(-t^2)*cos(a*t),t,w)); |

| > | convert(%,exp); |

liefert Gauß-Verteilung des Spektrums (incl. negative Frequenzen):
| > | a:=5: |
| > | plot(F,w=-10..10); |
![[Maple Plot]](fourier/fourier_1027.gif)
| > |
Umkehrung: Gauß-verteilte Frequenzen (ohne assume wird die Rücktransformation nicht durchgeführt)
| > | restart:with(inttrans):with(plots): |
| > | assume(sigma>0); |
| > | spek:=exp(-((w-w0)/sigma)^2/2)/sqrt(2*Pi)/sigma; |

| > | f:=invfourier(spek,w,t); |

Kontrolle der Normierung
| > | int(spek,w=-infinity..infinity); |
![]()
| > | int(f,t=-infinity..infinity); |
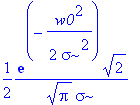
| > | int(evalc(abs(f)),t=-infinity..infinity); |
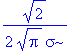
| > |
| > | #simplify(f); |
| > |
bzw. Probe durch Rücktransformation der Rücktransformierten: (bis auf 2*Pi)
| > | F:=fourier(f,t,w); |

| > | #simplify(F); |
| > |
| > |
| > |
| > |
| > | spek:=subs(sigma=sw,spek);f:=subs(sigma=sw,f); # um assume los zu werden |
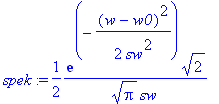
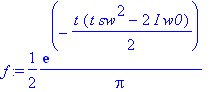
Gemeinsame Darstellung von Spektrum und Schwingung
| > | w0:=10: sw:=0.7: ref:=evalc(Re(f)): abf:=evalc(abs(f)): |
| > | psp:=plot(spek,w=0..20): #psp; |
| > | pf:=plot({ref,abf,-abf},t=-5..5): #pf; |
| > | display({pf,psp}); |
![[Maple Plot]](fourier/fourier_1036.gif)
(Z.z.: Das Produkt der Varianzen der beiden Gaußfunktionen ist 1.)
| > |
| > |
| > | w0:='w0': sw:='sw': |
| > | spek;f; |


| > | #combine(f,exp); |
| > | evalc(abs(f)); |

| > | absf:=combine(%,exp); |

| > |
| > | #convert(f,trig); |
| > | #convert(%,exp); |
| > | #expand(%); |
| > | spek; |
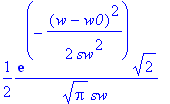
| > | ref:=simplify(evalc(Re(f))); |

| > | w0:=10: sw:=0.1: |
| > | pspek:=plot(spek,w=0..20):#pspek; |
| > | pf:=plot(ref,t=-10..10):#pf; |
| > | display(pf,pspek); |
![[Maple Plot]](fourier/fourier_1043.gif)
| > |
| > | sw:='sw':n:=20: |
| > | pspeks:=[seq(plot(spek,w=0..20),sw=seq(i/n,i=1..n))]: |
| > | #display(pspeks,insequence=true); |
| > |
| > |
| > | pfs:=[seq(plot(10*ref,t=-20..20),sw=seq(i/n,i=1..n))]: |
| > | #display(pfs,insequence=true); |
| > | display(seq(display([pfs[i],pspeks[i]]),i=1..n),insequence=true); |
![[Maple Plot]](fourier/fourier_1044.gif)
| > |
Natürlich gehört neben dem "Schwingungspaket" noch die Lorentz-Linie, also die Untersuchung von Resonanz mit Hilfe der Fouriertransformation ins Standardrepertoire:
| > | restart:with(inttrans): |
Gedämpfte Schwingung (vgl. Worksheets zu Differentialgleichungen)
| > | damp:=exp((-p/2+I*wurzel)*t); |

Fouriertransformierte
| > | assume(q>0,p>0,wurzel>0): |
| > | #p:='p':q:='q': |
| > | F:=fourier(damp*Heaviside(t),t,w); |
![]()
Betragsquadrat (mit gleichem Namen)
| > | F:=evalc(abs(F))^2; |
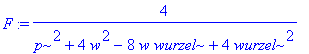
| > | #factor(denom(F)-p^2,w-wurzel); |
Gängige Darstellung
| > | with(student): |
| > | F:=completesquare(F,w); |

Assume~ loswerden:
| > | F:=subs(p=ph,F): p:='p': F:=subs(ph=p,F); |
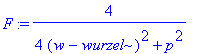
| > |
| > | F:=subs(wurzel=wh,F): wurzel:='wurzel': F:=subs(wh=wurzel,F); |
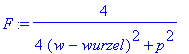
read(`fig.m`):winpl():vtitle:=Resonanzen:vxlab:=Frequenz: vylab:=A:
Darstellung von Resonanzkurven zu verschiedener Dämpfung
| > | q:='q': p:='p': |
| > | wurzel:=sqrt(4*q-p^2): |
| > | q:=10: |
pspl(`pfour6.ps`):
| > |
| > | seq(F,p=1..3); |
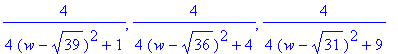
| > | wurzel; |
![]()
| > |
| > | F; |

| > | #plot({seq(F,p=1..3)},w=0..3*'wurzel'); |
| > |
| > | plot({seq(F,p=1..3)},w=0..20); |
![[Maple Plot]](fourier/fourier_1054.gif)
| > |
Hier noch eine Variante der Darstellung der Lorentz-Linie aus der Atomphysik, Gamma steht für die Zerfallskonstante eines Zustandes:
| > | restart;with(inttrans): |
| > | #Gamma:='Gamma': w0:='w0': |
| > | assume(Gamma>0,w0>0); |
| > | damp:=evalc(Re(exp(-w0*t*(I+Gamma/w0))))*Heaviside(t); |
![]()
| > | #damp:=t->((exp(-w0*t*(I+Gamma/w0))))*Heaviside(t); |
Alternative: statt Realteil negative Zeiten (mit der Funktion damp:=t->((exp ...)))
| > | #dampg:=(damp(t)-damp(-t))/2; |
| > | #dampmt:=damp(-t); |
| > | #F:=fourier(dampmt,t,w); |
| > | F:=fourier(damp,t,w); |
![]()
| > | Lorentz:=evalc(abs(op(2,F)))^2; |
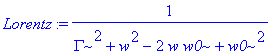
| > | with(student): |
| > | Lorentz:=completesquare(Lorentz,w); |

| > | Lorentz:=subs(w0=wh,Gamma=Gh,Lorentz): |
| > | unassign('w0','Gamma'): Lorentz:=subs(wh=w0,Gh=Gamma,Lorentz); |
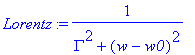
| > | Gamma:=3: w0:=10: w:='w': |
| > | plot(Lorentz,w=0..30); |
![[Maple Plot]](fourier/fourier_1060.gif)
| > | w0:='w0':Gamma:='Gamma': |
| > | f:=fourier(Lorentz,w,t); |
![]()
![]()
![]()
| > | Gamma:=3: w0:=10: |
| > | plot({evalc(Re(f)),evalc(abs(f)),-evalc(abs(f))},t=-5..5); |
![[Maple Plot]](fourier/fourier_1064.gif)
| > |
Und wir sind wieder bei einem Schwingungspaket angekommen ... allerdings nicht bei einem Gaußschen.
Die Lorentzlinie fällt für w-w0 = Gamma auf den halben Wert, man kann also Gamma mit der Linienbreite oder Frequenzunschärfe identifizieren
| > | w:=w0: Lorentz; |
![]()
| > | w:=w0-Gamma; Lorentz; |
![]()
![]()
| > | w:=w0+Gamma; Lorentz; |
![]()
![]()
Andererseits ist 1/Gamma die mittlere Lebensdauer (d.h. die Schwingung klingt in dieser Zeitspanne auf den e-ten Teil ab), so daß sich ergibt: Frequenzunschärfe mal Lebensdauer ~ 1.
Sie können diese Beziehung in den beiden vorangehenden Plots ausmessen, bzw. durch symbolische Rechnung überprüfen.
| > |
komma@oe.uni-tuebingen.de