Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 2.1.5 bis 2.1.7
Worksheet kino2_10.mws
| > |
c International Thomson Publishing Bonn filename: kino2.ms
Autor: Komma Datum: 14.6.94
Thema: Kinematik, beschleunigte Bewegung
Beschleunigte Bewegungen
Der Momentanwert der Änderung einer Größe ist die Ableitung dieser Größe nach der Zeit. Stellvertretend für den Momentanwert einer Änderung wird hier die Geschwindigkeit behandelt. Sie kann mit dem Befehl <diff definiert werden, auch wenn die Ortsfunktion noch nicht gegeben ist. Das ist auch zweckmäßig, wenn man keine frühe Bindung eingehen will, weil dann die Ortsfunktion später beliebig verändert werden kann, ohne daß die Geschwindigkeit neu zugewiesen werden muß.
| > | restart: with(plots): |
| > | v:=t->diff(x(t),t); |
![]()
| > |
Ortsfunktion:
| > | x:=t->t^3/5-t+3; |
![]()
| > |
Anhand der graphischen Darstellung läßt sich der Zusammenhang von Funktion und Ableitung leicht überprüfen:
| > | plot({x(t),v(t)},t=-2..4); |
![[Maple Plot]](kino2/kino2_103.gif)
| > |
Wir können diesen Zusammenhang geometrisch veranschaulichen, indem wir zunächst die Gleichung der Tangente (Punkt-Steigungsform) aufstellen. (Um flexibel zu bleiben, wird hier nicht der fertige Befehl <student[showtangent] verwendet).
| > | t0:='t0'; xt:='xt': |
![]()
| > | xt:=simplify(solve((xt-x(t0))/(t-t0)=v(t0),xt)); |
![]()
| > |
Diese Tangente kann nun im Punkt (t0|x(t0)) mit eingezeichnet werden. Dann muß ihre Steigung gleich v(t0) sein, was sich mit der Maus ausmessen läßt.
| > | t0:=2: |
| > | plot({x(t),v(t),xt},t=-2..4); |
![[Maple Plot]](kino2/kino2_106.gif)
| > |
Der Zeitpunkt t0 kann neu eingegeben und dann der Plot neu erstellt werden. Eine ander Ortsfunktion kann wegen der Formulierung von xt als Ausdruck nicht im nachhinein angegeben werden, bzw. wenn dies erwünscht ist, muß nach dem Löschen von xt das Assignment von xt neu abgearbeitet werden.
| > | # z.B. x:=t->t^2; xt:='xt': #zurueck zu xt:=...; |
Die Veranschaulichung gelingt besser, wenn wir ein Steigungsdreieck mit der Abszisse 1 einzeichnen (bei der Betrachtung auf die ggf. verschiedenen Maßstäbe von Abszisse und Ordinate achten, bzw. 1:1 wählen). Die Liste <dreieck wird von Maple im Plotbefehl automatisch als eine Aufzählung von Punkten interpretiert.
| > | t0:='t0': |
| > | dreieck:=[[t0,x(t0)],[t0,x(t0)-v(t0)],[t0-1,x(t0)-v(t0)]]; |
![]()
vtitle:=Steigungsdreieck:xtick:=1:pspl(`p2kino2.ps`):
| > | t0:=2: |
| > | plot({dreieck,x(t),xt,v(t)},t=-1..t0+2,color=black); |
![[Maple Plot]](kino2/kino2_108.gif)
| > |
| > |
Oder als Animation:
| > | t0:='t0':pd:=seq(plot({dreieck,x(t),xt,v(t)},t=-5..t0+2,-5..30,color=black),t0=seq(0.2*k,k=1..25)): |
| > |
| > | plots[display]([pd],insequence=true); |
![[Maple Plot]](kino2/kino2_109.gif)
| > |
Der Grundgedanke der Differential- und Integralrechnung
Die Details der Physik bleiben hier noch im Hintergrund. Es wird die Palette der Maple-Befehle vorgestellt. Aber der rote Faden ist die Infinitesimalrechnung, die hier "in erster Näherung" behandelt wird, d.h. "ersetze Kurve durch Gerade": die lineare Approximation mit Grenzübergang ist das A und O in der mathematischen Physik von Newton und Leibniz.
Wie kommt man (wie kamen Newton und Leibniz) auf Momentanwerte? Man geht von Mittelwerten aus und läßt das Zeitintervall gegen Null gehen. Ob die Natur es tatsächlich auch so macht, wie Leibniz das meinte ("natura non facit saltus") weiß man bis heute noch nicht, es erscheint aber nach der Quantenphysik und nun auch nach der Chaostheorie immer unwahrscheinlicher. Abgesehen davon: der Grenzwert bedeutet in der Regel eine Zahl mit unendlich vielen Stellen und wer kann schon mit dieser Genauigkeit rechnen (Rauschen des Kontinuums). Dennoch hat sich diese Mathematik glänzend bewährt, ja sie ist geradezu die Basis unserer heutigen technischen Gesellschaft.
Wir ersetzen zunächst die Ortsfunktion x(t) im Intervall [t , t+dt] durch eine gleichförmige Bewegung. Diese lineare Approximation ist in vielen folgenden Überlegungen und Beispielen ein elementarer Baustein und führt hier auf die mittlere Geschwindigkeit vq (wie im vorangehenden Abschnitt bei der stückweise gleichförmigen Bewegung).
| > | unassign('vq','x','dt','n','t1','t0','i'); |
| > | vq:=t->(x(t+dt)-x(t))/dt; |
![]()
Neugierige wollen sicher gleich wissen, wie sich aus diesem Differenzenquotient der Differentialquotient machen läßt. Dafür gibt es in Maple den Befehl <limit, der in diesem Fall die Ableitung in der Operatorschreibweise liefert:
| > | DQ:=limit(vq(t),dt=0); |
![]()
Testfunktion, Differenzenquotient und Differetialquotient:
| > | x:=t->t^5+t^2; |
![]()
| > | vq(t);DQ; |

![]()
| > |
Und wieder können Sie die letzten Befehle in Ihrem Worksheet überschreiben und damit testen, ob Maple auch tatsächlich die Regeln zur Berechnung von Grenzwerten beherrscht. Oder sind es die Regeln zur Differentiation?
Wir ersetzen nun die beschleunigte Bewegung durch eine stückweise gleichförmige, indem wir n Kurvenpunkte durch Sekanten verbinden. Dazu gibt es in Maple (mindestens) zwei Möglichkeiten. Die erste ist der <seq-Befehl:
| > | x:=t->1/5*t^3-t+3; #sin(t); |
![]()
| > | n:=5: |
| > | xliste:=[seq([i*dt,x(i*dt)],i=0..n)]; |
![]()
![]()
| > |
Der <seq-Befehel hat hier den Nachteil, daß vor seiner Ausführung n angegeben werden muß. Mit dem Wiederholungsoperator <$ läßt sich eine Liste variabler Länge leichter anlegen:
| > | n:='n': tt:=t0+j*dt: |
| > | xliste:=[[tt,x(tt)] $ j=0..n]; |
![xliste := [`$`([t0+j*dt, 1/5*(t0+j*dt)^3-t0-j*dt+3],j = 0 .. n)]](kino2/kino2_1018.gif)
| > | unassign('dt','t1','t0','n'): |
| > | dt:=(t1-t0)/n: |
vtitle:=`lin. Approx.`:pspl(`p3kino2.ps`):
| > | t1:=4: t0:=0: |
| > | n:=3: |
| > | plot({x(t),xliste},t=-2..t1); |
![[Maple Plot]](kino2/kino2_1019.gif)
| > |
Die zugehörigen mittleren Geschwindigkeiten können als Treppenfunktion dargestellt werden. (Alternative Formulierungen werden als Kommentare mitgeführt und können zum Experimentieren mit der Maple-Syntax verwendet werden.)
| > | stufe:=(a,b,c)->[[a,c(a)],[b,c(a)],[b,c(b)]]; |
![]()
| > | #treppe:=seq(stufe(t0+i*dt,t0+(i+1)*dt,vq),i=0..n); |
| > | n:='n': |
| > | treppe:=stufe(tt,tt+dt,vq) $ j=0..n; |
![treppe := `$`([[4*j/n, 1/4*(1/5*(4*j/n+4/n)^3-4/n-64/5*j^3/n^3)*n], [4*j/n+4/n, 1/4*(1/5*(4*j/n+4/n)^3-4/n-64/5*j^3/n^3)*n], [4*j/n+4/n, 1/4*(1/5*(4*j/n+8/n)^3-4/n-1/5*(4*j/n+4/n)^3)*n]],j = 0 .. n)](kino2/kino2_1021.gif)
![treppe := `$`([[4*j/n, 1/4*(1/5*(4*j/n+4/n)^3-4/n-64/5*j^3/n^3)*n], [4*j/n+4/n, 1/4*(1/5*(4*j/n+4/n)^3-4/n-64/5*j^3/n^3)*n], [4*j/n+4/n, 1/4*(1/5*(4*j/n+8/n)^3-4/n-1/5*(4*j/n+4/n)^3)*n]],j = 0 .. n)](kino2/kino2_1022.gif)
| > |
vtitle:=Differenzieren:xtick:=2:pspl(`p4kino2.ps`):
| > | n:=5: |
| > | plots[display]({plot({x(t),diff(x(t),t)},t=t0..t1),plot({treppe},t0..t1,color=red),plot({xliste},t=0..t1,color=blue)}); |
![[Maple Plot]](kino2/kino2_1023.gif)
| > |
Schon bei kleinen Werten von n läßt sich die angenäherte Ortsfunktion von der glatten (von Maple angenäherten) Kurve nicht mehr unterscheiden. Bei der Geschwindigkeit muß man schon zu höheren n-Werten greifen, wenn die Ableitungsfunktion wie eine stetige Kurve aussehen soll: das Differenzieren bringt die Näherung an den Tag.
Der letzte Plot zeigt den Zusammenhang von Funktion und Ableitung, bzw. in umgekehrter Richtung gelesen den Zusammenhang von Funktion und Stammfunktion ... wenn man sich jeweils den Grenzübergang dazudenkt. Läßt man den Grenzübergang aber bewußt weg, bleibt man also bei der deutlich sichtbaren linearen Approximation, und damit bei der stückweise gleichförmigen Bewegung, so ist die geometrische Bedeutung der Kurven unmittelbar klar: Die Steigung der Ortskurvenstücke ist der Funktionswert der Geschwindigkeitskurvenstücke. Umgekehrt muß dann die Fläche unter den Geschwindigkeitskurvenstücken den Funktionswert der Ortskurve ergeben ... bis auf eine additive Konstante. Summiert man also diese Flächen alle auf, so muß man den insgesamt zurückgelegten Weg erhalten.
| > | i:='i': n:='n':t0:='t0':t1:='t1': |
| > | xq:=sum(vq(t0+i*dt),i=0..n-1)*dt; |

| > |
Der insgesamt zurückgelegte Weg darf aber bei dem gemachten Ansatz nicht von der Anzahl der Wegstücke abhängen:
| > | simplify(%); |

| > | (x(t1)-x(t0))-xq; |
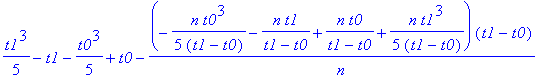
| > | simplify(%); |
![]()
| > |
Oder zum Experimentieren mit konkreten Zahlen n:
| > | x(t); |
![]()
| > | n:=5: xq; |
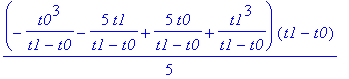
| > | simplify(%); |

| > |
Anstatt verschiedene n einzugeben, können wir Maple auch den Grenzwert berechnen lassen. Das ist bei dem gemachten Ansatz zwar nicht besonders sinnvoll, weil sich die Terme mit n herausheben, die Befehle werden aber der Vollständigkeit halber aufgeführt:
| > | n:='n': |
| > | lxq:=limit(xq,n=infinity); |

| > | x(t1)-x(t0)-lxq; |

| > | #simplify(%); |
| > |
Wenn wir umgekehrt die Funktion für die Momentangeschwindigkeit vorgeben wollen, um von ihr auf die Ortsfunktion zu schließen, können wir so vorgehen:
| > | unassign('v','x','dt','n','t1','t0','i'); |
| > |
Wie oben, nur jetzt mit allgemeinem v(t)
| > | xq:=sum(v(t0+i*dt),i=0..n-1)*dt; |

| > |
Bildung des Grenzwertes:
| > | dt:=(t1-t0)/n; |
![]()
| > | lxq:=limit(xq,n=infinity); |

| > |
Angabe einer Funktion (wenn Sie sin(t) zur Funktion hinzufügen, wird die Ausgabe etwas länger):
| > | v:=t->3/5*t^2-1; # +sin(t); |
![]()
| > | xq; |

| > | lxq; |
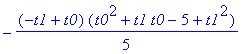
| > | expand(lxq); |
![]()
| > |
So berechnet man also ohne einen Integrationsbefehl ein bestimmtes Integral.
Die Graphische Darstellung von Momentangeschwindigkeit und mittlerer Geschwindigkeit können wir im wesentlichen von oben übernehmen:
| > | v:='v': |
| > | tt:=t0+j*dt: |
| > | stufe:=(a,b,c)->[[a,c(a)],[b,c(a)],[b,c(b)]]; |
![]()
| > | #treppe:=seq(stufe(t0+i*dt,t0+(i+1)*dt,vq),i=0..n); |
| > | n:='n': |
| > | treppe:=stufe(tt,tt+dt,v) $ j=0..n; |
![]()
![]()
| > |
Zur Abwechslung einmal eine etwas seltenere Funktion:
| > | v:=t->2^t; |
![]()
vtitle:=`momentanes Mittel`:vylab:=`v `:ytick:=3:pspl(`p5kino2.ps`):
| > | t0:=0: t1:=4: |
| > | n:=50: |
| > | plots[display]({plot({treppe},t=t0..t1,color=red),plot(v(t),t=t0..t1,color=blue)}); |
![[Maple Plot]](kino2/kino2_1044.gif)
| > |
Natürlich wieder verschiedene n testen!
Für die angenäherte Ortsfunktion stellen wir zunächst eine Liste der variablen Länge n+1 parat
| > | n:='n': tt:=t0+j*dt: |
| > | xliste:=[[tt,x[j]] $ j=0..n]; |
![]()
Und berechnen deren Elemente in einer <for-Schleife
| > | t0:=0: t1:=4: |
| > | x0:=10: |
| > | x[0]:=x0: |
| > | n:=50: |
| > | for i to n do |
| > | x[i]:=x[i-1]+v(t0+i*dt)*dt: |
| > | od: |
Schauen Sie sich die Liste ruhig an ...
| > | #xliste; |
Und verändern Sie in der vorigen Region n ...
vtitle:=Genauigkeit: pspl(`p6kino2.ps`):
| > | plot({xliste,int(v(tau),tau=0..t)+x0},t=t0..t1); |
![[Maple Plot]](kino2/kino2_1046.gif)
| > |
Im Plot-Befehl ist schon die exakte Lösung eingebaut, die Stammfunktion lautet:
| > | int(v(tau),tau=0..t); |

Noch einmal der Vergleich mit dem Grenzwert:
| > | i:='i': n:='n': t1:='t': dt:='dt':t0:=0: |
| > | xq:=Sum(v(t0+i*dt),i=0..n-1)*dt; |

| > | xq:=value(xq); |

| > | dt:=(t1-t0)/n: |
| > | lxq:=limit(xq,n=infinity); |

Anmerkung: xq wird hier in zwei Schritten "berechnet": <Sum ist die träge (inert) Version von <sum und hindert Maple an der Vereinfachung der Summe, die dann mit <value erreicht wird.
| > |
Statistik-Befehle:
Für die Behandlung der stückweise gleichförmigen Bewegung (oder allgemeiner von diskreten Funktionen) kann das <stats-Paket eingesetzt werden
| > | restart: |
| > | with(stats): with(describe): with(statplots): with(plots): |
| > |
Mittelwerte
Die Geschwindigkeit v wird als zeitliche Ableitung einer noch unbekannten Ortsfunktion vordefiniert. Die Ortsfunktion kann dann beliebig vorgegeben werden. Zur Darstellung der Geschwindigkeit einer stückweise gleichförmigen Bewegung in n Abschnitten kann der <histogram-Befehl verwendet werden (Normierung am einfachsten mit dt). Die mittlere Geschwindigkeit erhält man mit <mean.
| > | v:=t->diff(x(t),t); |
![]()
| > | x:=t->sin(t)^2; |
![]()
| > | n:=50: dt:='dt': |
Aufbau der Liste für das v-t-Histogramm
| > | liste:=[seq(Weight(t..t+dt,dt*evalf(subs(th=t,v(th)))),t=seq(dt*i,i=0..n))]: |
Liste der Geschwindigkeiten zur Bildung des Mittelwertes vq (kann auch zur Darstellung des v-Histogrammes benutzt werden):
| > | vliste:=[seq(subs(th=t,v(th)),t=seq(dt*i,i=0..n))]: |
| > | vq:=mean(vliste): |
| > |
In den vorangehenden Befehlen wurde t verwendet und muß nun wieder freigegeben werden:
| > | t:='t': # ohne das funktioniert diff nicht ... HAUEFIGER FEHLER! |
| > | v(t); |
![]()
Kontrollen:
| > | #liste; |
| > | #dt:=.1: |
| > | #vliste; |
| > |
read (`fig.m`):opt2d;winpl():
vtitle:=Zusammenfassung:xtick:=0:ytick:=0:pspl(`p7kino2.ps`):
Darstellung der Ortsfunktion x(t), der Geschwindigkeitsfunktion v(t) und ihrer Annäherung durch Mittelwerte der <liste, sowie der mittleren Geschwindigkeit vq. (Sie können im Plotfenster <style=line wählen.)
| > | dt:=.01: |
| > | display({display(histogram(liste),style=line),plot({x(h),v(h),vq},h=0..n*dt,color=red)}); |
![[Maple Plot]](kino2/kino2_1054.gif)
| > |
Kontrolle:
| > | vq; |
![]()
| > | (x(n*dt)-x(0))/(n*dt); |
![]()
| > | int(v(u),u=0..n*dt)/(n*dt); |
![]()
| > |
Kurvenfit
Man kann aber mit dem <stats-package nicht nur Histogramme zeichnen und Mittelwerte bilden. Eine der wohl wichtigsten Anwendungen für den Physiker ist der Kurvenfit experimentell gewonnener Daten. Angenommen, man vermutet einen quadratischen Zusammenhang zwischen zwei Meßgrößen, weiß aber nicht, ob systematische Fehler wie z.B. eine Verschiebung des Nullpunkts oder ein linearer Anteil vorhanden ist, so kann man mehrere Ansätze machen und mit einem leastsquare-fit vergleichen:
Die Meßreeihe wird in der Form [Abszissenwerte], [Ordinatenwerte] eingegeben:
| > | reihe:=[1,2,3.1,4],[2.9,6.2,11,18]; |
![]()
Drei Ansätze
| > | ansatz1:=x=a*t^2; |
![]()
| > | ansatz2:=x=a*t^2+c; |
![]()
| > | ansatz3:=x=a*t^2+b*t+c; |
![]()
und die zugehörigen Fits
| > | kurve1:=fit[leastsquare[[t,x],ansatz1]]( [reihe]); |
![]()
| > | kurve2:=fit[leastsquare[[t,x],ansatz2]]( [reihe]); |
![]()
| > | kurve3:=fit[leastsquare[[t,x],ansatz3]]( [reihe]); |
![]()
vtitle:=Fit:xtick:=2:ytick:=2:vxlab:=t:vylab:=x:pspl(`p8kino2.ps`):
| > | plots[display]({plot(rhs(kurve1),t=0..5,-10..10), |
| > | plot(rhs(kurve2),t=0..5,-10..10), |
| > | plot(rhs(kurve3),t=0..5,-10..10),display(statplots[scatterplot](reihe),symbol=box)}); |
![[Maple Plot]](kino2/kino2_1065.gif)
| > |
| > |
Oder liegt ein exponentieller Zusammenhang vor?
| > | a:='a':b:='b': |
| > | kurve:=fit[leastsquare[[t,x],x=a*exp(t)+b,{a,b}]]( [reihe]); |
![]()
| > | display({plot(rhs(kurve),t=0..5,-10..10),statplots[scatterplot](reihe)}); |
![[Maple Plot]](kino2/kino2_1067.gif)
| > |
Wenn man im letzten Beispiel einen der Parameter in {a,b} wegläßt, so bleibt er in der Lösung frei verfügbar.
| > | kurve:=fit[leastsquare[[t,x],x=a*exp(t)+b,{a}]]( [reihe]); |
![]()
| > |
und man kann von Hand weitere Untersuchungen anstellen
| > | b:=5; |
![]()
| > | kurve; |
![]()
| > | display({plot(rhs(kurve),t=0..5,-10..10),statplots[scatterplot](reihe)}); |
![[Maple Plot]](kino2/kino2_1071.gif)
| > |
| > |
| > |
| > |
komma@oe.uni-tuebingen.de