![[Maple Plot]](newton1/newton1_101.gif)
Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 2.2, S. 60 bis 71
Worksheet newton1_10.mws
| > |
c International Thomson Publishing, Bonn 1995 filename: newton1.ms
Autor: Komma Datum: 30.4.94
Thema: Newtons Physik
Anmelden der Packages
| > | restart;with(linalg):with(student):with(plots): |
| > |
Newtons Bewegungsgleichung kann als eine mächtige Maschine aufgefaßt werden, die ALLES verarbeitet. Womit wird diese Maschine gefüttert und was produziert sie? Der Input ist ein Kraftgesetz und Anfangsbedingungen, der Output ist die zugehörige Bahn. Wir wollen die Maschine nur in diese Richtung arbeiten lassen, denn die Umkehrung ist entweder trivial (zweimalige Differentiation der bekannten Ortsfunktion für die Kraft längs der Bahn) oder nicht eindeutig lösbar, wenn man unter Kraftgesetz das Kraftfeld versteht. In der folgenden Animation können Sie allerdings durch einen einfachen Klick die Maschine vorwärts und rückwärts laufen lassen.
| > | step:=0.5: n:=20: nstep:=n*step: |
| > | klist:=[seq(display({plot(0.5*x*Heaviside(x-2)*sin(x-delta*2*Pi/nstep),x=-2..15), |
| > | textplot([1,sin(2*Pi*delta/nstep),`F=m*a`],color=red), |
| > | textplot([8*(1-delta/nstep),8*(1-delta/nstep),`Anfangsbedingungen`],color=blue), |
| > | textplot([-2*(1-delta/nstep),5*(1-delta/nstep),`Kraftgesetz`],color=blue)}), |
| > | delta=seq(i*step,i=1..n))]: |
| > |
| > | #plot(0.5*x*Heaviside(x-2)*sin(x-5*2*Pi/nstep),x=-2..15); |
| > |
| > |
| > |
| > |
read `fig.m`:
vtitle:=Maschine:pspl(`p0new1.ps`):#winpl():
replot(klist[8],opt2d,axes=none,font=[HELVETICA,30]); winpl():
| > | display(klist,insequence=true,axes=none); |
![[Maple Plot]](newton1/newton1_101.gif)
| > |
(Im Folgenden wird der <vector-Befehl/Typ verwendet)
Wenn wir die Bewegung eines Massenpunktes untersuchen wollen, müssen wir zunächst den Ort als Funktion der Zeit definieren:
| > | r:=vector([x(t),y(t),z(t)]); |
![]()
In dieser Definition werden die Ausdrücke x(t), y(t) und z(t) von Maple als (noch unbekannte) Funktionen erkannt:
| > | whattype(r[1]); |
![]()
Mit der map-Funktion bilden wir die erste und zweite Ableitung von r(t) nach der Zeit und erhalten so die Definition der Geschwindigkeit v(t) und der Beschleunigung a(t):
| > | v:=map(diff,r,t); |
![]()
| > | a:=map(diff,v,t); |
![a := vector([diff(x(t),`$`(t,2)), diff(y(t),`$`(t,2)), diff(z(t),`$`(t,2))])](newton1/newton1_105.gif)
Wir stellen noch einen Kraftvektor bereit, dessen Komponenten Fx, Fy, Fz später durch die Angabe eines Kraftgesetzes belegt werden können:
| > | F:=vector([Fx,Fy,Fz]); |
![]()
Die Bewegungsgleichung läßt sich nun mit dem Befehl "student[equate]" aufstellen
| > | sys:=equate(m*a,F); |

Im Prinzip ist das schon die ganze Maschine, aber sie läuft noch nicht. Doch dafür haben wir ja Maple.
| > | sol:=dsolve(sys,{x(t),y(t),z(t)},method=laplace); |
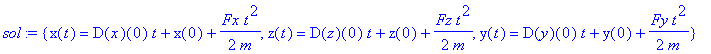
Wenn wir keine besonderen Angaben zu den Kraftkomponenten machen, werden sie bei der Lösung der Differentialgleichnug als konstant angenommen.
Der Zusatz (option) "laplace" hat zwei große Vorteile gegenüber der "normalen" Lösung von "sys" mit "dsolve":
erstens wird so die Lösung wesentlich schneller gefunden, zweitens wird sie gleich mit Anfangsbedingungen dargestellt.
Wir kontrollieren:
| > | x(t); |
![]()
Die Funktionen sind noch nicht zugewiesen worden, aber das läßt sich mit einem Befehl beheben:
| > | assign(sol); |
| > | x(t); |
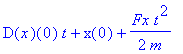
Wie sieht der Vektor r aus?
| > | r;op(r);eval(r); r[1];map(eval,r); |
![]()
![]()
![]()
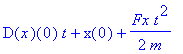
![vector([D(x)(0)*t+x(0)+1/2*Fx*t^2/m, D(y)(0)*t+y(0)+1/2*Fy*t^2/m, D(z)(0)*t+z(0)+1/2*Fz*t^2/m])](newton1/newton1_1015.gif)
Oder...
| > | v; eval(v); map(eval,v); map(eval,a); |
![]()
![]()
![]()
![]()
Man möchte nun natürlich gerne den Output der Newton-Maple-Maschine zu bestimmten Zeiten sehen, also kann man versuchen:
| > | x(7); |
![]()
Aber x(7) ist nur eine neuer unbekannter Funktionsname und
| > | subs(t=7,x(t)); |
![]()
| > |
funktioniert zwar, ist aber zum Schreiben zu schwerfällig. Doch es gibt einen praktischen Befehl im <student-package, nämlich <makeproc (VORSICHT: x = makeproc(x...) würde zu einem stack-overflow führen, deshalb die neuen Namen):
| > | xx:=makeproc(x(t),t); yy:=makeproc(y(t),t); zz:=makeproc(z(t),t); |
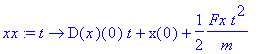
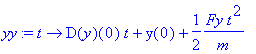
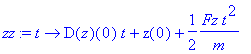
| > | xx(7); |
![]()
Das geht auch kompakter:
| > | rf:=makeproc(map(eval,r),t); vf:=makeproc(map(eval,v),t); af:=makeproc(map(eval,a),t); |
![rf := t -> [D(x)(0)*t+x(0)+1/2*Fx*t^2/m, D(y)(0)*t+y(0)+1/2*Fy*t^2/m, D(z)(0)*t+z(0)+1/2*Fz*t^2/m]](newton1/newton1_1026.gif)
![]()
![]()
| > | rf(TESTZEIT)[2]; vf(TESTZEIT)[1]; af(TESTZEIT)[3]; |
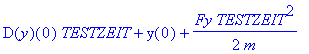
![]()
![]()
Doch nun ist es Zeit konkret zu werden. Wir können als erstes Beispiel den Wurf untersuchen. Damit man wieder von hier aus loopen kann, werden die rechten Seiten als unausgewertete Ausdrücke ('...') gesetzt.
| > | Fx:=0: Fy:=0: Fz:='-m*g'; |
![]()
Eine etwas gängigere Schreibweise für die Anfangsbedingungen, die den erwünschten Nebeneffekt hat, daß die Funktionen in voller Allgemeinheit weiterverarbeitet werden können.
| > | x(0):='x0': D(x)(0):='vx0': y(0):='y0': D(y)(0):='vy0':z(0):='z0': D(z)(0):='vz0'; |
![]()
Anfangswerte:
| > | x0:=0: vx0:=4: y0:=0: vy0:=6:z0:=0: vz0:=7: |
| > | m:=4: g:=10: |
Kontrolle der Funktionen (bei der Auswertung (z.B. beim plot) von rf werden die Werte von x0 ... übertragen)
| > | rf(t); map(eval,rf(t));vf(t); af(t); |
![]()
![]()
![]()
![]()
Graphische Darstellung:
| > | myoptions:=axes=normal,labels=['x','y','z'],orientation=[-48,75],scaling=constrained: |
| > | spacecurve(rf(t),t=0..2,myoptions); |
![[Maple Plot]](newton1/newton1_1038.gif)
Und vor der Arbeit das Spiel:
| > | display([seq(spacecurve(rf(t),t=0..0.1*i),i=1..20)],insequence=true,myoptions); |
![[Maple Plot]](newton1/newton1_1039.gif)
| > |
Das geht natürlich vorwärts und rückwärts ... wegen der Zeitsymmetrie.
Die einfachsten Aufgaben bestehen nun darin, die Anfangsbedingungen und die Kraftkomponenten zu ändern. Zunächst spielerisch in den Befehlen (Kraft und Anfangsbedingungen) von oben ("was ändert sich wenn ... ") und dann gezielt mit Gleichungen. So kann man sich z.B. fragen:
1.) Wo liegt der Auftreffpunkt in der x-y-Ebene?
| > | print(rf(t)); |
![]()
Die z-Koordinate muß Null sein. Das ist der Fall für die Zeiten
| > | treff:=solve(zz(t),t); |
![]()
| > | xx(7/5); yy(7/5); |
![]()
![]()
also konkret:
| > | eval(xx(7/5)); eval(yy(7/5)); |
![]()
![]()
Man kann die Elemente der Menge {treff} mit dem <op-Befehl übernehmen. Doch dabei ist Vorsicht geboten:
1.) Behandelt Maple Mengen wirklich wie Mengen, d.h. ungeordnet - und zwar je nach "innerem Zustand" (Speicher, Reihenfolge der Abarbeitung der Befehle, ....), man kann sich also nicht darauf verlassen, daß ein Element immer wieder am gleichen Platz erscheint.
2.) Stimmt die Ausgabe nicht mit dem "inneren Zustand" überein:
| > | op({treff}); |
![]()
Der <op-Befehl erfordert also immer Mitdenken und Kontrolle des aktuellen Zustandes
| > | punkt:=eval(subs(t=op(2,{treff}),rf(t))); # op(1/2, .. ist von Maples internem Zustand abhängig ... |
![punkt := [14/5-2/5*49^(1/2), 21/5-3/5*49^(1/2), 49/10-7/10*49^(1/2)-5*(7/10-1/10*49^(1/2))^2]](newton1/newton1_1047.gif)
Eine "wasserdichte Programmierung" wäre zwar möglich (Abfrage der Argumente), lohnt sich aber hier nicht.
1.a) Wie groß ist die Wurfweite?
| > | sqrt(dotprod(punkt,punkt)); |
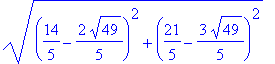
| > | norm(punkt,2); |
![]()
1.b) Betrag und Winkel der Geschwindigkeit für t = treff? WIEDER VORSICHT MIT op!!!!
| > | vtreff:=vf(op(2,{treff})); |
![]()
| > | norm(vtreff,2); |
![]()
| > | angle(vector(vtreff),vector([1,0,0])); # die Liste vtreff wird nicht akzeptiert!? |
![]()
| > | evalf(%*180/Pi); |
![]()
Wer's nicht glaubt, kann es im Plot nachmessen (plot geeignet drehen und kontrollieren, ob 1:1 aktiviert ist).
2.) Steigzeit und Steihöhe bzw. Scheitelpunkt?
Die z-Komponente der Geschwindigkeit muß Null sein:
| > | vf(t); |
![]()
| > | steig:=solve(vf(t)[3],t); |
![]()
Stimmt! Das ist die halbe Wurfdauer ... es ist doch beruhigend, wenn man etwas im Kopf nachrechnen kann.
| > | eval(zz(steig)); eval(rf(steig)); # wem das eval lästig ist, der kann bei D(x)(0) ... bleiben |
![]()
![]()
Zur Ergänzung nun noch die Darstellung von Ort und Geschwindigkeit als Funktionen der Zeit.
Für den, der alles gleich auf einmal sehen will und noch ein paar neue Maple-Befehle kennenlernen will, so formuliert:
vtitle:=`Eine Menge`:vxlab:=t:ytick:=0:pspl(`p2new1.ps`):
| > | plot(convert(eval(rf(t)),set) union convert(eval(vf(t)),set),t=0..2); |
![[Maple Plot]](newton1/newton1_1058.gif)
| > |
Die Stärke eines CAS liegt im Spiel mit Parametern und der leichten Formulierbarkeit inverser Problemstellungen.
3.) Stelle (alle) Bahnen mit gleicher Anfangsgeschwindigkeit dar,
| > | vz0:=v0*sin(winkel()[1]): vx0:=v0*cos(winkel()[1])*cos(winkel()[2]):vy0:=v0*cos(winkel()[1])*sin(winkel()[2]): |
| > | winkel:=proc() evalm(randvector(2)*Pi/100) end; |
![]()
| > | feuerwerk:=seq(eval(rf(t)),i=1..10): |
| > | v0:=15: |
vtitle:=Feuerwerk:pspl(`p3new1.ps`):
| > | spacecurve({feuerwerk},t=0..5,scaling=constrained,orientation=[70,80]); |
![[Maple Plot]](newton1/newton1_1060.gif)
Und natürlich ...
| > | display([seq(spacecurve({feuerwerk},t=0..0.1*i),i=1..5)],insequence=true,style=wireframe); |
![[Maple Plot]](newton1/newton1_1061.gif)
| > |
4.) Wie muß man beim Abschuß vom Ursprung die Startgeschwindigkeit wählen, damit der Punkt (x1|y1|z1) erreicht wird?
(Die ballistische Kurve kommt später ...).
| > | rf(t); # es kann mit x0... Probleme geben, wenn man das worksheet neu oeffnet und nicht von vorne abarbeitet !?! |
![]()
| > | ziel:=vector([x1,y1,z1]); |
![]()
| > | zielsys:=equate(rf(t),ziel); |
![]()
Da stehen vom letzten Plot noch feste Werte drin, also Rücksetzen von v0:
| > |
| > | unassign('vx0','vy0','vz0','v0','x1','y1','z1','t1'); |
| > | zielsys:=equate(rf(t),ziel); |
![]()
Man sieht: es fehlt noch eine Bedingung.
4.a) das Ziel soll zu vorgegebener Zeit t1 erreicht werden.
| > | tzielsys:=zielsys union {t=t1}; |
![]()
| > | solt:=solve(tzielsys,{vx0,vy0,vz0,t}); |
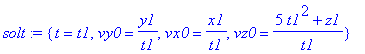
4.b) der Betrag der Startgeschwindigkeit ist gegeben (oder die Startenergie)
| > | vzielsys:=zielsys union {v0^2=vx0^2+vy0^2+vz0^2}; |
![]()
| > | unassign('vx0','vy0','vz0','t','v0','z1','x1','y1'); |
| > | solv:=solve[radical](vzielsys,{vx0,vy0,vz0,t}); |
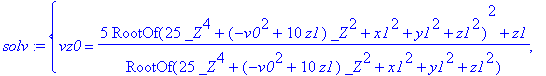
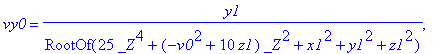
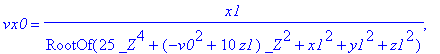
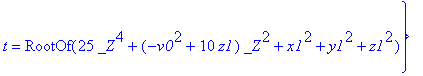
| > | assign(solv); |
| > | allvalues(t); |
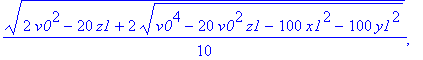
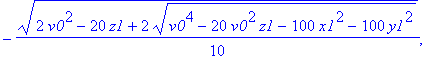
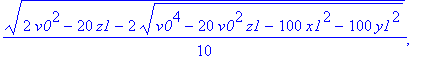
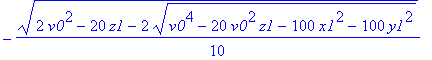
Zur besseren Übersicht zweidimensional (y-z-Ebene), und Treffpunkt auf der y-Achse, mit der Fragestellung: welche Mindestgeschwindigkeit ist erforderlich?
| > | z1:=0: x1:=0: |
| > | zeiten:=allvalues(t); |
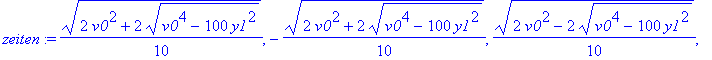
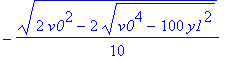
Es kommen also vier Zeitpunkte in Frage (zwei in der Zukunft und zwei in der Vergangenheit). Dazu gehören z.B. in y-Richtung die vier Geschwindigkeitskomponenten.
| > | t:='t': |
| > | allvalues(vy0); |
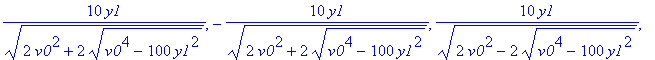
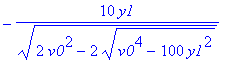
Wir setzen die ersten beiden in die Ortsfunktion ein # Vorsicht: Nummerierungen nicht stabil
| > | bahn[1]:=subs('vy0'=allvalues(vy0)[1],'vz0'=allvalues(vz0)[1],rf(t)); #das macht man mit |
![bahn[1] := [vx0*t+x0, 10*y1/(2*v0^2+2*(v0^4-100*y1^2)^(1/2))^(1/2)*t+y0, 1/2*(2*v0^2+2*(v0^4-100*y1^2)^(1/2))^(1/2)*t+z0-5*t^2]](newton1/newton1_1081.gif)
| > | bahn[2]:=subs('vy0'=allvalues(vy0)[4],'vz0'=allvalues(vz0)[4],rf(t)); #copy und paste |
![bahn[2] := [vx0*t+x0, -10*y1/(2*v0^2-2*(v0^4-100*y1^2)^(1/2))^(1/2)*t+y0, -1/2*(2*v0^2-2*(v0^4-100*y1^2)^(1/2))^(1/2)*t+z0-5*t^2]](newton1/newton1_1082.gif)
| > | #rf(t); |
Und zeichenen ein paar Bahnen
| > | v00:=sqrt(10*y1): |
| > | v0:='v0':y1:=3: |
vtitle:=Steilschuss:vxlab:=x:ytick:=2:vylab:=y:pspl(`p4new1.ps`):
| > | plot({seq([bahn[1][2],bahn[1][3],t=0..zeiten[1]],v0=seq(v00+i*0.1*v00,i=0..3))},scaling=constrained); |
![[Maple Plot]](newton1/newton1_1083.gif)
vtitle:=Flachschuss:pspl(`p5new1.ps`):
| > | plot({seq([bahn[2][2],bahn[2][3],t=0..zeiten[4]],v0=seq(v00+i*0.1*v00,i=0..3))},scaling=constrained); |
![[Maple Plot]](newton1/newton1_1084.gif)
| > |
Wenn man die Plots am Scheitel mit der Maus ausmißt, stellt man fest, daß sie eine Kurve gemeinsam haben.
Das ist die Kurve mit 45° Startwinkel und die mit der kleinsten Startgeschwindigkeit.
Zum Schluß noch eine kleine Fingerübung: Wie lautet die Bahngleichung z = z(y) für die Bewegung in der y-z-Ebene?
| > | 'z'=subs(t=solve(yy(t)='y',t),zz(t)); |
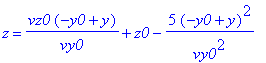
| > |
| > |
komma@oe.uni-tuebingen.de