newton2_10.mws

Moderne Physik mit Maple

PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 2.2 Seite 72 bis 75

Worksheet newton2_10.mws

>   

c International Thomson Publishing Bonn      1995                      filename: newton2.ms

Autor: Komma                                                                             Datum: 1.5.94

Thema: Newtons Physik, Teilchen in Feldern

Newtons Maschine ist nicht zu stoppen!

>    restart;with(linalg):with(student):with(plots):

>    r:=vector([x(t),y(t),z(t)]);

r := vector([x(t), y(t), z(t)])

>    v:=map(diff,r,t);

v := vector([diff(x(t),t), diff(y(t),t), diff(z(t),t)])

>    a:=map(diff,v,t);

a := vector([diff(x(t),`$`(t,2)), diff(y(t),`$`(t,2)), diff(z(t),`$`(t,2))])

Definition der Felder:

>    El:=vector([Ex,Ey,Ez]);

El := vector([Ex, Ey, Ez])

>    B:=vector([Bx,By,Bz]);

B := vector([Bx, By, Bz])

Lorentzkraft:

>    F:=q*(El+crossprod(v,B));

F := q*(El+vector([diff(y(t),t)*Bz-diff(z(t),t)*By, diff(z(t),t)*Bx-diff(x(t),t)*Bz, diff(x(t),t)*By-diff(y(t),t)*Bx]))

>    evalm(%);

vector([q*(Ex+diff(y(t),t)*Bz-diff(z(t),t)*By), q*(Ey+diff(z(t),t)*Bx-diff(x(t),t)*Bz), q*(Ez+diff(x(t),t)*By-diff(y(t),t)*Bx)])

Bewegungsgleichung:

>    sys:=equate(m*a,F);

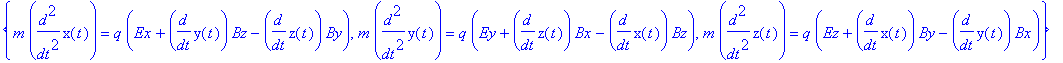
sys := {m*diff(x(t),`$`(t,2)) = q*(Ex+diff(y(t),t)*Bz-diff(z(t),t)*By), m*diff(y(t),`$`(t,2)) = q*(Ey+diff(z(t),t)*Bx-diff(x(t),t)*Bz), m*diff(z(t),`$`(t,2)) = q*(Ez+diff(x(t),t)*By-diff(y(t),t)*Bx)}
sys := {m*diff(x(t),`$`(t,2)) = q*(Ex+diff(y(t),t)*Bz-diff(z(t),t)*By), m*diff(y(t),`$`(t,2)) = q*(Ey+diff(z(t),t)*Bx-diff(x(t),t)*Bz), m*diff(z(t),`$`(t,2)) = q*(Ez+diff(x(t),t)*By-diff(y(t),t)*Bx)}

Lösung: (Bitte warten ...)

>    sol:=dsolve(sys,{x(t),y(t),z(t)},method=laplace): ## mit sinh

>    #convert(sol,exp);

>    assign(sol);

>    xx:=makeproc(x(t),t):  yy:=makeproc(y(t),t):  zz:=makeproc(z(t),t):

>    #xx(t);

Lösungsfunktion (da lacht das Herz des theoretischen Physikers, aber es wäre eine Aufgabe für sich, mit einem CAS und Termmanipulation die relevanten Terme herauszuschälen - siehe Jackson).

>    rf:=makeproc(map(eval,r),t): vf:=makeproc(map(eval,v),t): af:=makeproc(map(eval,a),t):

B-Feld in z-Richtung (zur besseren Übersicht):

>    Bx:=0:By:=0:

>    rf(ZEIT);

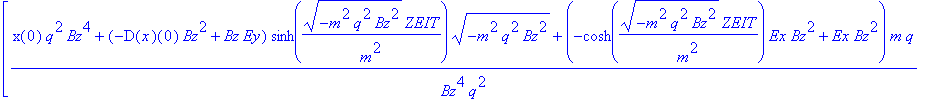
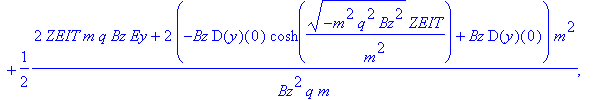
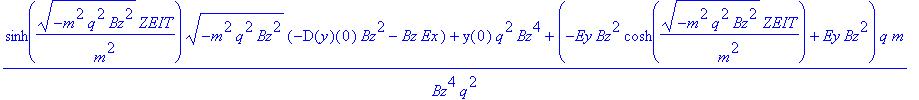
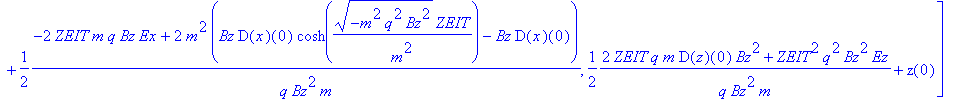
[(x(0)*q^2*Bz^4+(-D(x)(0)*Bz^2+Bz*Ey)*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+(-cosh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*Ex*Bz^2+Ex*Bz^2)*m*q)/Bz^4/q^2+1/2*1/Bz^2*(2*ZEIT*m*q*Bz*Ey+2*(-B...
[(x(0)*q^2*Bz^4+(-D(x)(0)*Bz^2+Bz*Ey)*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+(-cosh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*Ex*Bz^2+Ex*Bz^2)*m*q)/Bz^4/q^2+1/2*1/Bz^2*(2*ZEIT*m*q*Bz*Ey+2*(-B...
[(x(0)*q^2*Bz^4+(-D(x)(0)*Bz^2+Bz*Ey)*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+(-cosh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*Ex*Bz^2+Ex*Bz^2)*m*q)/Bz^4/q^2+1/2*1/Bz^2*(2*ZEIT*m*q*Bz*Ey+2*(-B...
[(x(0)*q^2*Bz^4+(-D(x)(0)*Bz^2+Bz*Ey)*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+(-cosh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*Ex*Bz^2+Ex*Bz^2)*m*q)/Bz^4/q^2+1/2*1/Bz^2*(2*ZEIT*m*q*Bz*Ey+2*(-B...

Namensgebung:

>    x(0):=x0: D(x)(0):=vx0: y(0):=y0: D(y)(0):=vy0:z(0):=z0: D(z)(0):=vz0;

D(z)(0) := vz0

elektrische Feldstärke:

>    Ex:=0: Ey:=-5:Ez:=1/10: simplify(rf(ZEIT));

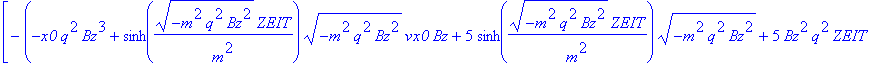
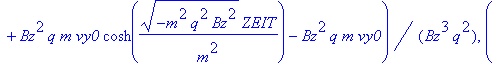
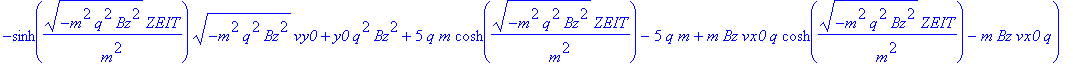
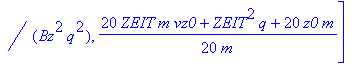
[-1/Bz^3*(-x0*q^2*Bz^3+sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)*vx0*Bz+5*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+5*Bz^2*q^2*ZEIT+Bz^2*q*m*vy0*cosh((-m^2*q^2*Bz^2)^(...
[-1/Bz^3*(-x0*q^2*Bz^3+sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)*vx0*Bz+5*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+5*Bz^2*q^2*ZEIT+Bz^2*q*m*vy0*cosh((-m^2*q^2*Bz^2)^(...
[-1/Bz^3*(-x0*q^2*Bz^3+sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)*vx0*Bz+5*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+5*Bz^2*q^2*ZEIT+Bz^2*q*m*vy0*cosh((-m^2*q^2*Bz^2)^(...
[-1/Bz^3*(-x0*q^2*Bz^3+sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)*vx0*Bz+5*sinh((-m^2*q^2*Bz^2)^(1/2)/m^2*ZEIT)*(-m^2*q^2*Bz^2)^(1/2)+5*Bz^2*q^2*ZEIT+Bz^2*q*m*vy0*cosh((-m^2*q^2*Bz^2)^(...

Anfangswerte und Konstanten:

>    x0:=0: vx0:=0: y0:=0: vy0:=10:z0:=0: vz0:=0:

>     q:=1: m:=1: Bz:=2:

read `fig.m`:winl():

vtitle:=Elektronenbahn:xtick:=2:vxlab:=``:vylab:=y:vzlab:=z:pspl(`p1new2.ps`):


Jetzt geht's los!

>    myoptions:=axes=normal,labels=['x','y','z'],orientation=[-48,75],scaling=constrained,numpoints=400,color=red:

>   

>    rf(t);

[x0+1/16*(-4*vx0-10)*sinh((-4)^(1/2)*t)*(-4)^(1/2)-5/2*t-1/2*vy0*cosh((-4)^(1/2)*t)+1/2*vy0, -1/4*sinh((-4)^(1/2)*t)*(-4)^(1/2)*vy0+y0+5/4*cosh((-4)^(1/2)*t)-5/4+1/2*vx0*cosh((-4)^(1/2)*t)-1/2*vx0, t*v...
[x0+1/16*(-4*vx0-10)*sinh((-4)^(1/2)*t)*(-4)^(1/2)-5/2*t-1/2*vy0*cosh((-4)^(1/2)*t)+1/2*vy0, -1/4*sinh((-4)^(1/2)*t)*(-4)^(1/2)*vy0+y0+5/4*cosh((-4)^(1/2)*t)-5/4+1/2*vx0*cosh((-4)^(1/2)*t)-1/2*vx0, t*v...

>   

>    eval(rf(t));

[5-5/8*sinh((-4)^(1/2)*t)*(-4)^(1/2)-5/2*t-5*cosh((-4)^(1/2)*t), -5/2*sinh((-4)^(1/2)*t)*(-4)^(1/2)-5/4+5/4*cosh((-4)^(1/2)*t), 1/20*t^2]

>    evalc((rf(t)));

[x0-(-1/4*vx0-5/8)*sin(4^(1/2)*t)*4^(1/2)-5/2*t-1/2*vy0*cos(4^(1/2)*t)+1/2*vy0, 1/4*sin(4^(1/2)*t)*4^(1/2)*vy0+y0+5/4*cos(4^(1/2)*t)-5/4+1/2*vx0*cos(4^(1/2)*t)-1/2*vx0, t*vz0+1/20*t^2+z0]

>   

>    spacecurve(evalc(rf(t)),t=0..20,myoptions);

[Maple Plot]

>   

Aber wer gibt sich schon mit so einem einfachen statischen Bild zufrieden?

>    display([seq(spacecurve(evalc(rf(t)),t=0..i),i=1..20)],insequence=true,myoptions);

[Maple Plot]

>   

Und schon sind wir mitten in der Elektrodynamik / Magnetohydrodynamik / Relativitätstheorie. Ein Versehen? Nein, das passiert nun mal, wenn man mit diesen Maschinen arbeitet wie von selbst. Newtons Maschine und die Maple-Maschine verleiten zu einer tour d'horizon durch die Physik. Mit diesem Werkzeug (Maple) kann man das Experiment am Computer durchführen und so "mit Formeln forschen" ... wenn man sie hat und versteht.

>   

>   

>   

komma@oe.uni-tuebingen.de