newtpro_10.html

newtpro_10.mws

Moderne Physik mit Maple

PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 2.2.2

Worksheet newtpro_10.mws

>

c International Thomson Publishing Bonn 1995 filename: newtpro.ms

Autor: Komma Datum: 4.5.94

Thema: Newtons Physik als procedure. Das Worksheet enthält die procedure newton zur geschlossenen Lösung der Bewegungsgleichung und Anwendungsbeispiele.

Benötigte packages

> restart;with(linalg):with(student):with(plots):

Beginn der Prozedur

> newton:=proc(F) global r,v,a,xx,yy,zz,rf,vf,af,sol,sys;

> #with(linalg):with(student):with(plots):readlib(unassign):

> #unassign('x(t)','y(t)','z(t)');

Es ist zweckmäßig, auch die Anfangsbedingungen zurückzusetzen, damit die Lösung jeweils in allgemeiner Form zur Verfügung steht, und konkrete Werte außerhalb der Prozedur und ohne neuen Aufruf eingesetzt werden können. Die Übergabe der Anfangsbedingungen als Parameter der Prozedur wäre möglich, würde aber zuviel Schreibarbeit beim Aufruf oder eine Abfrage der Argumente erfordern. Die Ortsfunktionen müssen wegen sys (s.u.) zurückgesetzt werden.

Ein konsequentes Umgehen der frühen Bindung durch einführen weiterer Prozeduren würde die Übersichtlichkeit nicht erhöhen. In diesem Stadium genügt die Methode: "mache aus einem funktionierenden worksheet durch "proc() ... end;"

eine Prozedur.

> unassign('x(t)','y(t)','z(t)','x0','vx0','y0','vy0','z0','vz0');

> #x(0):='x0': D(x)(0):='vx0': y(0):='y0': D(y)(0):='vy0':z(0):='z0': D(z)(0):='vz0';

> r:=vector([x(t),y(t),z(t)]);

> v:=map(diff,r,t);

> a:=map(diff,v,t);

Wenn sys in der proc steht und diese mehrfach aufgerufen wird, müssen vorher die Ortsfunktionen mit unassign zurückgesetz werden. (s.o.)

> sys:=equate(m*a,F);

> #print(sys);

>

> sol:=dsolve(sys,{x(t),y(t),z(t)},method=laplace);

> print(sol);

> if sol=NULL then sol:=dsolve(sys,{x(t),y(t),z(t)}) fi;

> if sol=NULL then RETURN(`keine Loesung gefunden`) fi;

> assign(sol);

> xx:=makeproc(x(t),t): yy:=makeproc(y(t),t): zz:=makeproc(z(t),t):

> rf:=makeproc(map(eval,r),t); vf:=makeproc(map(eval,v),t); af:=makeproc(map(eval,a),t);

> x(0):='x0': D(x)(0):='vx0': y(0):='y0': D(y)(0):='vy0':z(0):='z0': D(z)(0):='vz0';

> RETURN(op(rf));

> end;

>

> #x(t):='x(t)':y(t):='y(t)':

> unassign('x(t)','y(t)','z(t)');

Wenn im Kraftgesetz bereits zugewiesene Variable verwendet werden (z.B. x(t), v(t).. ), ist es am einfachsten, diese nicht ausgewertet, also in '..' aufzuführen. Alternative: kleine Löschprozedur. Am Beispiel der gedämften Schwingung (in x-Richtung), der eine konstante Kraft überlagert ist und einer gleichmäßig beschleunigten Bewegung in y- und z-Richtung kann man die Formeln studieren, die von Maple geliefert werden. Natürlich kann man auch den Input ändern.

> unassign('Fx','Fy','Fz'):

> F:=vector([Fx-'x(t)+v[1]',Fy,Fz]);

>

> newton(F);

${z(t) = D(z)(0)*t+z(0)+1/2*Fz*t^2/m, x(t) = Fx+(x(0)-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m)+(2*m*D(x)(0)+x(0)-Fx)/(1-4*m)^(1/2)*sinh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m), y(t) = D(y)(0)*t+y(0)+1...$
${z(t) = D(z)(0)*t+z(0)+1/2*Fz*t^2/m, x(t) = Fx+(x(0)-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m)+(2*m*D(x)(0)+x(0)-Fx)/(1-4*m)^(1/2)*sinh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m), y(t) = D(y)(0)*t+y(0)+1...$

t -> [Fx+(x(0)-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m)+(2*m*D(x)(0)+x(0)-Fx)/(1-4*m)^(1/2)*sinh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m), D(y)(0)*t+y(0)+1/2*Fy*t^2/m, D(z)(0)*t+z(0)+1/2*Fz*t^2/m]

> rf(t);

[Fx+(x0-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m)+(2*m*vx0+x0-Fx)/(1-4*m)^(1/2)*sinh(1/2*t/m*(1-4*m)^(1/2))*exp(-1/2*t/m), vy0*t+y0+1/2*Fy*t^2/m, vz0*t+z0+1/2*Fz*t^2/m]

> vf(t);

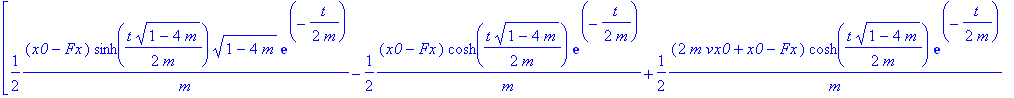
[1/2*(x0-Fx)*sinh(1/2*t/m*(1-4*m)^(1/2))*(1-4*m)^(1/2)/m*exp(-1/2*t/m)-1/2*(x0-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))/m*exp(-1/2*t/m)+1/2*(2*m*vx0+x0-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))/m*exp(-1/2*t/m)-1/2*(2*m*v...

> af(t);

[1/4*(x0-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))*(1-4*m)/m^2*exp(-1/2*t/m)-1/2*(x0-Fx)*sinh(1/2*t/m*(1-4*m)^(1/2))*(1-4*m)^(1/2)/m^2*exp(-1/2*t/m)+1/4*(x0-Fx)*cosh(1/2*t/m*(1-4*m)^(1/2))/m^2*exp(-1/2*t/m)+1/4*...

>

read `fig.m`:winpl():

> m:=1: x0:=0: vx0:=2: Fx:=0:

vtitle:=`x(t), v(t), a(t)`:vxlab:=t:vylab:=``:pspl(`p1newpro.ps`):

> plot({rf(t)[1],vf(t)[1],af(t)[1]},t=0..15);

[Maple Plot]

>

> #unassign('x(t)','y(t)','z(t)','x0','vx0','y0','vy0','z0','vz0');

Und mit dem parametrischen Plot ein Phasenportrait:

pspl(`p2newpro.ps`):vtitle:=`v-x-Diagramm`:vxlab:=x:vylab:=v:

> plot([rf(t)[1],vf(t)[1],t=0..15]);

[Maple Plot]

>

komma@oe.uni-tuebingen.de