Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 3.1.1
Worksheet oszi_10.mws
| > |
International Thomson Publishing, Bonn 1995 filename: oszi.ms
Autor: Komma Datum: 7.8.94
Thema: Berechnug und Darstellung der Überlagerung von Schwingungen
Die Schwingungsgleichung kann als wichtiger Sonderfall der Newtonschen Bewegungsgleichung angesehen werden, oder -- mathematisch gesehen -- als gewöhnliche DG 2.Ordnung. Die Bestimmung der Lösung wird deshalb in den entsprechenden Abschnitten behandelt. An dieser Stelle geht es darum, wie man die als gegeben vorausgesetzten Lösungen darstellt und mit Maple handhabt. Wir wollen mit der Überlagerung zweier Schwingungen beginnen.
| > | restart; with(plots): |
| > | x1:=a1*sin(omega*t-phi); |
![]()
| > | x2:=a2*sin(Omega*t); |
![]()
| > | x:=x1+x2; |
![]()
| > | a1:=2: a2:=.4: phi:=Pi/2: Omega:=2: omega:=Omega/5: |
| > | p1:=plot(x1,t,color=red): |
| > | p2:=plot(x2,t,color=green): |
| > | p3:=plot(x,t): |
| > | display({p1,p2,p3}); |
![[Maple Plot]](oszi/oszi_104.gif)
| > |
Animation zu verschiedenen Phasen
| > | phi:='phi': |
| > | animate(x,t=-10..10,phi=0..2*Pi-0.1,numpoints=200); |
![[Maple Plot]](oszi/oszi_105.gif)
| > |
Der Sonderfall der Schwebung mit a2=a1 und fast gleichen Frequenzen.
| > | a1:='a1': a2:=a1: omega:='omega': Omega:='Omega': phi:='phi': x:=x1+x2; # manchmal -a1*sin... |
![]()
Mit Hilfe des <trigsubs-Befehles können wir die Umformung der Summe in ein Produkt erreichen. Dazu muß allerdings erst durch a1 dividiert werden, weil sonst eine Fehlermeldung kommt (und x darf nicht als Diffrenz dargestellt sein):
| > |
| > | x:=a1*op(trigsubs(simplify(x/a1))); |
![]()
| > |
Die Cosinus-Funktion kann als zeitabhängige Amplitude aufgefaßt werden, die Sinusfunktion beschreibt dann die Phase:
| > | ampl:=x/op(3,x); # Numerierung nicht stabil! |
![]()
| > | #ampl:=2*a1*cos(1/2*omega*t-1/2*phi-1/2*Omega*t); |
| > | phase:=op(3,x); |
![]()
| > | #phase:=sin(1/2*omega*t-1/2*phi+1/2*Omega*t); |
Plot der beiden Faktoren und des Produktes:
| > | phi:=0: Omega:=5: omega:=.9*Omega: a1:=1: |
| > | plot({ampl,phase,x},t); |
![[Maple Plot]](oszi/oszi_1010.gif)
| > |
Animation der Schwebungskurve:
| > | phi:='phi': |
| > | animate(x,t=-10..10,phi=0..2*Pi-.1,numpoints=200,color=green); |
![[Maple Plot]](oszi/oszi_1011.gif)
| > |
Von einem Oszilloskop kann z.B. eine Folge von Momentaufnahmen gemacht werden:
| > | Omega:=5: omega:=0.9*Omega: |
| > | t:='t': ts:='ts': phi:=0: |
| > | aniampl:=subs(t=ts,ampl); |
![]()
| > | plot({seq(aniampl*phase,ts=1..8)},t=-2..2); |
![[Maple Plot]](oszi/oszi_1013.gif)
| > |
Animation der Momentaufnahmen (beim Oszilloskop müßte man sich mit der Triggerung Mühe geben):
| > | ps:=seq(plot(aniampl*phase,t=-2..2),ts=seq(i*2*Pi/(Omega-omega)/10,i=0..19)): |
| > | display([ps],insequence=true); # [ ] für richtige Reihenfolge |
![[Maple Plot]](oszi/oszi_1014.gif)
| > |
Berücksichtigung der Dämpfung:
Die anderen Größen wieder unassignen (mit einer kleinen procedure, weil das öfter vokommt):
| > | unas:=proc() unassign('omega','Omega','phi','k','a1'): end: unas(); |
| > | d:=exp(-k*t); |
![]()
| > | xd:=x1*d; |
![]()
| > | a1:=2: |
| > | omega:=5: # 5 |
| > | k:=1/4: # 1/4 |
| > | phi:=0: |
| > | xd; |
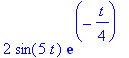
Plot der gedämpften Schwingung mit Einhüllender:
| > | plot({xd,a1*d,-a1*d},t=0..20); |
![[Maple Plot]](oszi/oszi_1018.gif)
| > |
Phasenportraits (v-x-Diagramme) zunächst ohne Dämpfung:
| > | v1:=diff(x1,t); |
![]()
| > | plot([x1,v1,t=0..1],scaling=constrained); |
![[Maple Plot]](oszi/oszi_1020.gif)
| > |
| > | phi:=Pi/3: plot([x1,v1,t=0..1]); |
![[Maple Plot]](oszi/oszi_1021.gif)
| > |
räumliche Darstellung der Phasenkurve:
| > | spacecurve([t,v1,x1],t=0..5,axes=boxed,numpoints=100); |
![[Maple Plot]](oszi/oszi_1022.gif)
| > |
Verbindung der Kurvenpunkte mit der t-Achse
| > | cylinderplot([z,t/2,t],t=0..20,z=0..5); # Verbindung der spacecurve (von oben) mit der Zeitachse (senkrecht) |
![[Maple Plot]](oszi/oszi_1023.gif)
| > |
Phasenportraits mit Dämpfung:
| > | unas(); |
| > | vd:=diff(xd,t); |
![]()
| > | a1:=1: omega:=5: k:=1/4: phi:=0: |
| > | plot([xd,vd,t=0..5]); |
![[Maple Plot]](oszi/oszi_1025.gif)
| > |
| > | #with(plots): # gehört endlich in den .ini-file od. zusammen mit restart! |
| > | spacecurve([t,vd,xd],t=0..5,axes=boxed,numpoints=100); |
![[Maple Plot]](oszi/oszi_1026.gif)
| > |
| > | k:=.1: |
| > | cylinderplot([z*exp(-k*t),t/2,t],t=0..20,z=0..5); |
![[Maple Plot]](oszi/oszi_1027.gif)
| > |
Lissajousfiguren (mit Dämpfung, falls erwünscht):
| > | #restart: with(plots): |
| > | x:=ax*exp(-kx*t)*sin(ox*t+px); |
![]()
| > | y:=ay*exp(-ky*t)*cos(oy*t+py); |
![]()
| > | ax:=1: kx:=0.2: ox:=1: px:=0: |
| > | ay:=1: ky:=0: oy:=4: py:=0: |
| > | plot([x,y,t=0..2*Pi/ox]); |
![[Maple Plot]](oszi/oszi_1030.gif)
| > |
In Bewegung:
| > | px:='px': |
| > | animate([x,y,t=0..2*Pi/ox],px=0..Pi,numpoints=100); |
![[Maple Plot]](oszi/oszi_1031.gif)
| > |
"räumliche Lissajous-Figuren":
| > | setoptions3d(axes=boxed); |
| > | px:=0: |
| > | spacecurve([cos(ox*t),sin(ox*t),y],t=0..2*Pi,axes=boxed,numpoints=100); |
![[Maple Plot]](oszi/oszi_1032.gif)
| > |
In Bewegung
| > | i:='i': py:=0: px:=i*Pi/20: ox:=1: |
| > | sl:=seq(spacecurve([cos(ox*t+px),sin(ox*t+px),y],t=0..2*Pi,axes=boxed,numpoints=100),i=1..20): |
| > | display3d([sl],insequence=true); |
![[Maple Plot]](oszi/oszi_1033.gif)
| > |
Epizyklen in komplexer Schreibweise:
| > | restart;with(plots): |
| > | o1:=r1*exp(I*Omega*t); |
![]()
| > | o2:=r2*exp(I*omega*t); |
![]()
| > | o:=o1+o2; |
![]()
| > | theta:=argument(o); |
![]()
| > | r:=abs(o); |
![]()
| > | r1:=2: Omega:=-1: # auch negative Kreisfrequenzen sind erlaubt |
| > | r2:=1: omega:=7: |
Plot in Polarkoordinaten (mit Zeitmessung):
| > | setoptions(scaling=constrained); |
| > | start:=time(); |
![]()
| > | polarplot([evalc(r),evalc(theta),t=0..2*Pi]); |
![[Maple Plot]](oszi/oszi_1040.gif)
| > | dauer:=time()-start; |
![]()
| > |
Parameterplot:
| > | y:=evalc(Im(o)); x:=evalc(Re(o)); |
![]()
![]()
| > | start:=time(); |
![]()
| > | plot([x,y,t=0..2*Pi]); |
![[Maple Plot]](oszi/oszi_1045.gif)
| > | dauer:=time()-start; |
![]()
| > |
| > |
| > |
komma@oe.uni-tuebingen.de