PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 5.2.3

Worksheet rydb_10.mws

c International Thomson Publishing, Bonn 1995            filename: rydb

Autor: Komma                                                             Datum: 11.94

Thema: Quasiklassisches Atom

Synopsis: Wellenpaket mit Dispersion

Zeitliche Entwicklung im Laborsystem und im SPS des Paketes.

Überlappung des zerfließenden Paketes auf Kreisbahn: Interferenz.

Animation des "Rydberg/Landau-Atoms".

>	restart; with(plots):

Gaußpaket

>	psi:=1/s*exp(-X/(2*a^2*s^2));

mit komplexer Varianz (vgl. paket1.ms)

>	s:=sqrt(1+I*t/a^2);

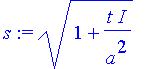
>	X:=x^2-2*I*a^2*k*x+I*a^2*k^2*t;

Das Betragsquadrat wird schnell berechnet

>	apsi:=simplify(evalc(abs(psi))^2);

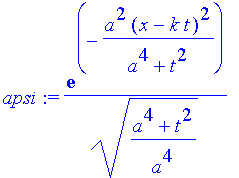
Der Realteil ist etwas umfangreicher, (auch mit assume a>0)

>

a:='a':

>	#assume(a>0):

>	rpsi:=evalc(Re(psi));

>

Die Vereinfachung dauert recht lange und man bekommt das überflüssige (?) csgn nicht weg. Außerdem hängt die Reaktion von simplify davon ab, ob das .m-file mit eingelesen wurde!! (Restart ändert daran nichts). Das Ergebnis der Vereinfachung wurde deshalb via lprint in das Worksheet übernommen, um den Term schnell zur Verfügung zu haben.

rpsi:=simplify(rpsi);

Sicherung des flüchtigen vereinfachten rpsi:

lprint(rpsi);

-1/2*(-(2*((a^4+t^2)/a^4)^(1/2)+2)^(1/2)*cos(1/2*(-2*a^4*k*x+a^4*k^2*t-x^2*t)/(
a^4+t^2))+csgn(t-I*a^2)*(2*((a^4+t^2)/a^4)^(1/2)-2)^(1/2)*sin(1/2*(-2*a^4*k*x+a
^4*k^2*t-x^2*t)/(a^4+t^2)))*exp(-1/2*a^2*(-x+k*t)^2/(a^4+t^2))/((a^4+t^2)/a^4)^
(1/2)

>	a:='a': k:='k': x:='x': t:='t':

>	safe:=-1/2*(-(2*((a^4+t^2)/a^4)^(1/2)+2)^(1/2)*cos(1/2*(-2*a^4*k*x+a^4*k^2*t-x^2*t)/(

>	a^4+t^2))+csgn(t-I*a^2)*(2*((a^4+t^2)/a^4)^(1/2)-2)^(1/2)*sin(1/2*(-2*a^4*k*x+a

>	^4*k^2*t-x^2*t)/(a^4+t^2)))*exp(-1/2*a^2*(-x+k*t)^2/(a^4+t^2))/((a^4+t^2)/a^4)^

>

(1/2);

>	k:=5: a:=1: t:=1:

>	plot(safe,x=-20..20);

>

t:='t':

animate(rpsi,x=-20..20,t=-2..2,numpoints=200);

ENTSTEHUNG und Zerfall des Wellenpaketes

>	t:='t':k:=5:a:=1:fsafe:=evalf(safe);# am schnellsten ca. 2min.

Sie können sich die Berechnung sparen, wenn Sie zum read-Befehl weitergehen und pak1.m (mit der richtigen Pfadangabe) einlesen.

>	paket1:=animate(fsafe,x=-20..20,t=-2..2,numpoints=200):

save paket1,`pak1.m`;

>	#read `pak1.m`;

>

paket1;

>

Wir wollen nun dieses zerfließende Paket auf eine Kreisbahn setzen. Dann wird früher oder später die Front das Ende einholen und überholen und dabei das Paket "mit sich selbst interferieren".

Die Transformation in das SPS (Schwerpunktsystem) des Paketes erleichtert das Vorgehen:

(x=x+kt nicht in apsi od. rpsi substituieren!)

>	a:='a':k:='k':t:='t':

>	sapsi:=simplify(evalc(abs(subs(x=x+k*t,psi))));

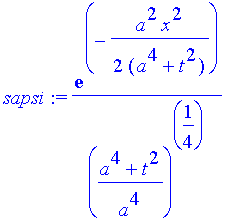
>	srpsi:=evalc(Re(subs(x=x+k*t,rpsi)));

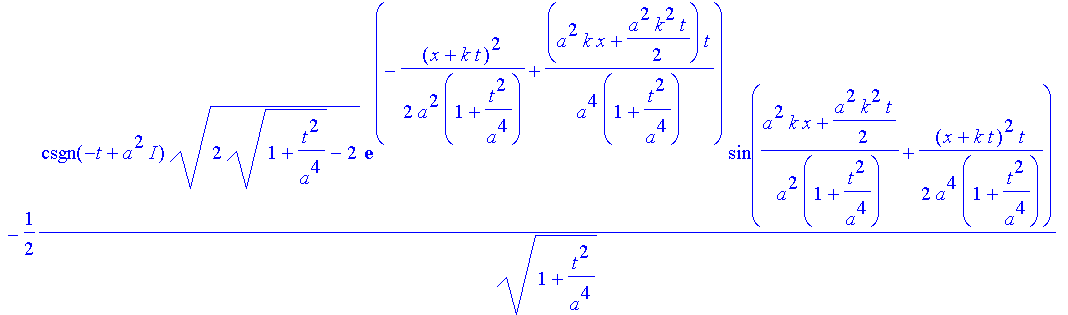
Die vereinfachte Version:

lprint(srpsi);

-1/2*(-(2*(1+t^2/a^4)^(1/2)+2)^(1/2)*cos((-a^4*k*x-1/2*a^4*k^2*t-1/2*(x+k*t)^2*
t)/(a^4+t^2))+1/2*csgn(t-I*a^2)*abs(2*(1+t^2/a^4)^(1/2)-2)^(1/2)*(1+signum(2*(1
+t^2/a^4)^(1/2)-2))*sin((-a^4*k*x-1/2*a^4*k^2*t-1/2*(x+k*t)^2*t)/(a^4+t^2)))*
exp(-1/2*a^2*x^2/(a^4+t^2))/(1+t^2/a^4)^(1/2)

>	safe2:=-1/2*(-(2*(1+t^2/a^4)^(1/2)+2)^(1/2)*cos((-a^4*k*x-1/2*a^4*k^2*t-1/2*(x+k*t)^2*

>	t)/(a^4+t^2))+1/2*csgn(t-I*a^2)*abs(2*(1+t^2/a^4)^(1/2)-2)^(1/2)*(1+signum(2*(1

>	+t^2/a^4)^(1/2)-2))*sin((-a^4*k*x-1/2*a^4*k^2*t-1/2*(x+k*t)^2*t)/(a^4+t^2)))*

>	exp(-1/2*a^2*x^2/(a^4+t^2))/(1+t^2/a^4)^(1/2);

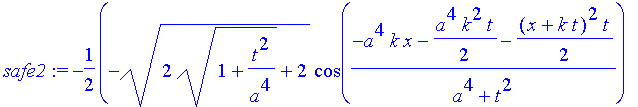
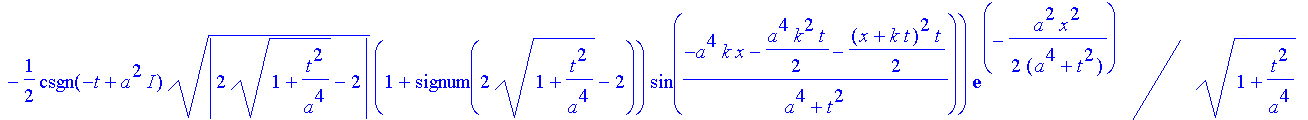
Signum(..) ist überflüssig, die Klammer (1+signum) ergibt außer für t=0 immer 2. Für t=0 wird aber die Wurzel davor 0.

(Zeit-)Probleme mit simplify von Re ... kommt wohl von signum und csgn (s.o.)

>	#srpsi:=simplify(srpsi);

>	srpsi:=safe2:

Entstehung und Zerfall des Wellenpaketes im SPS. Bei den Signum-Entscheidungen wird viel Zeit verbraucht

>	t:='t':a:=1: k:=2:

>	animate(sapsi,x=-20..20,t=-10..10,numpoints=100,color=red);

>

>	paket2:=animate(srpsi,x=-20..20,t=-10..10,numpoints=100,color=red):

>

paket2;

save paket2,`pak2.m`;

>	#read `pak2.m`;

>

#paket2;

Nach diesen Kontrollplots, die noch einmal schön demonstrieren, wie die Anteile mit kuzer Wellenlänge die mit langer überholen, können wir die Überlappung behandeln.

Interferenz durch Überlappung beim Zerfliessen im SPS

Substitution x=x+k*t in psi selbst (nicht in Re und abs).

>	k:='k':a:='a':t:='t':

>

psi;

>	spsi:=simplify(subs(x=x+k*t,psi));

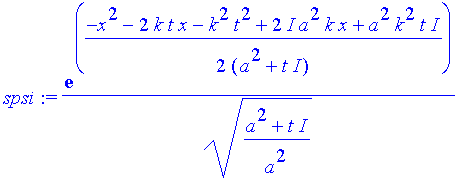
>	n:='n':x0:='x0':a:='a':k:='k': t:='t':

"Partialwelle" zur n-ten Überlappung

>	part:=subs(x=x+2*n*x0,spsi);

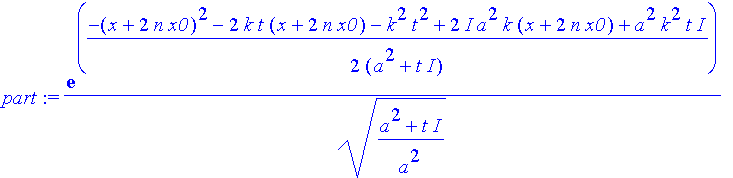
Blende zum Ausschneiden von -x0 bis x0

>

x0:='x0':

>	blende:=Heaviside(x+x0)-Heaviside(x-x0);

>

x0:=2:

>	plot(blende,x=-10..10);

>

Kontrolle der "Partialwellenbeträge" (manchmal taucht nach simplify csgn auf)

>

n:=0:

>	sapsi;simplify(evalc(abs(part)));

(Die Partialwelle wird leicht verschoben gezeichnet, für n=0)

>	n:=0:a:=2:k:=2:t:=0:

>	plot({sapsi+0.01,evalc(abs(part))},x=-10..10);

>

Überlappung:

Wenn Sie sich ein Wellenpaket auf einen Streifen Papier malen (eine Folie wäre besser), aus diesem Streifen einem Ring machen und den Ring dann platt drücken, sollten Sie etwa folgendes Bild sehen (das nicht aufgewickelte Paket ist mit eingezeichnet)

>	plot({sapsi,blende*sapsi,seq(blende*evalc(abs(part)),n=-2..2)},x=-10..10,color=red);

>

für Abbildung p1rydb:=":save p1rydb, `abbryd.m`:

Interferenz der 'Partialwellen'

(Für die Summenbildung zur Interferenz kann die Vereinfachung - z.B. von rpsi - nicht verwendet werden)

>	n:='n':t:='t':a:='a':k:='k':x0:='x0':

>	sumpsi:=blende*sum(part,n=-2..2);

>

sumpsi;

Vermutung: Mit dem Umfang u=2x0 und der Umlaufsdauer T=2x0/k sollten Wiederholungen zu Vielfachen von T auftreten, wenn man x0=n*l wählt, mit l=2Pi/k.

Das Aufsummieren sollte nach der 2..3-sigma-Regel geschehen, mit dem zeitabhängigen sigma=a*sqrt(1+t^2/a^4) also n=(2..3)sigma/x0.

Ein Kontrollplot vor der Animation

>

n:='n':

>	t:=0:a:=2:k:=2:x0:=2*Pi/k:

>	plot(evalc(abs(sumpsi)),x=-10..10);

>

Ohne Termvereinfachung dauert die Berechnung der beiden nächsten Plots recht lange

t:='t':

animate(evalc(abs(sumpsi)),x=-6..6,t=0..5,frames=5);

t:='t':

plot3d(evalc(abs(sumpsi)),x=-6..6,t=-1..20);

Deshalb lohnt sich die folgende Vereinfachung sehr (auch wenn man bei simplify warten muß). Allerdings läßt sich dann der Laufbereich der Summation nicht mehr flexibel programmieren.

>	a:='a':t:='t':n:='n':k:='k':x0:='x0':

evalc(abs(sumpsi)):

simplify("):

asumpsi:=":

lprint(asumpsi);

>

Hier ist das Ergebnis, das Sie mit Return "abarbeiten" müssen, wenn Sie weiterkommen wollen

>

>	safe3:=1/(a^4+t^2)^(1/4)*((Heaviside(x+x0)-Heaviside(x-x0))^2*(2*exp(-a^2*(x^2+6*x*x0+10*x0^2

>	)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*

>	x+8*k*t^2*x0+k^2*t^3)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*k^2*t+x^2*t+4*t*x*

>	x0+4*t*x0^2+2*k*t^2*x+4*k*t^2*x0+k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(x^2-6*x*x0+10*x0^2)/(

>	a^4+t^2))*sin(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*t+4*t*x*x0-4*t*x0^2-2*k*t^2*x+4

>	*k*t^2*x0-k^2*t^3)/(a^4+t^2))*sin(1/2*(-2*a^4*k*x+8*a^4*k*x0-a^4*k^2*t-x^2*t+8*t*x*x0-

>	16*t*x0^2-2*k*t^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2))-2*exp(-a^2*(x^2+4*x0^2)/(a^4+t^2))*

>	sin(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*k^2*t+x^2*t+4*t*x*x0+4*t*x0^2+2*k*t^2*x+4*k*t^2*x0+k

>	^2*t^3)/(a^4+t^2))*sin(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*t+4*t*x*x0-4*t*x0^2-2*

>	k*t^2*x+4*k*t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(x^2+2*x*x0+10*x0^2)/(a^4+t^2))*cos(

>	1/2*(2*a^4*k*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t^2*x0+k^2*

>	t^3)/(a^4+t^2))*cos(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*t+4*t*x*x0-4*t*x0^2-2*k*t

>	^2*x+4*k*t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(x^2+4*x*x0+8*x0^2)/(a^4+t^2))*sin(1/2*

>	(2*a^4*k*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t^2*x0+k^2*t^3)

>	/(a^4+t^2))*sin(1/2*(2*a^4*k*x+a^4*k^2*t+2*k*t^2*x+k^2*t^3+x^2*t)/(a^4+t^2))-2*exp(-a^

>	2*(x^2-2*x*x0+10*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*k^2*t+x^2*t+4*t*x*

>	x0+4*t*x0^2+2*k*t^2*x+4*k*t^2*x0+k^2*t^3)/(a^4+t^2))*sin(1/2*(-2*a^4*k*x+8*a^4*k*x0-a^

>	4*k^2*t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(

>	x^2-2*x*x0+10*x0^2)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*k^2*t+x^2*t+4*t*x*x0+

>	4*t*x0^2+2*k*t^2*x+4*k*t^2*x0+k^2*t^3)/(a^4+t^2))*cos(1/2*(-2*a^4*k*x+8*a^4*k*x0-a^4*k

>	^2*t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(x^2

>	-2*x*x0+2*x0^2)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+a^4*k^2*t+2*k*t^2*x+k^2*t^3+x^2*t)/(a^4+

>	t^2))*cos(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*t+4*t*x*x0-4*t*x0^2-2*k*t^2*x+4*k*t

>	^2*x0-k^2*t^3)/(a^4+t^2))-2*exp(-a^2*(x^2-4*x*x0+8*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4*k*x

>	+a^4*k^2*t+2*k*t^2*x+k^2*t^3+x^2*t)/(a^4+t^2))*sin(1/2*(-2*a^4*k*x+8*a^4*k*x0-a^4*k^2*

>	t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(x^2+2*

>	x*x0+2*x0^2)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*k^2*t+x^2*t+4*t*x*x0+4*t*x0^

>	2+2*k*t^2*x+4*k*t^2*x0+k^2*t^3)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+a^4*k^2*t+2*k*t^2*x+k^2*

>	t^3+x^2*t)/(a^4+t^2))+2*exp(-a^2*(x^2+4*x0^2)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+4*a^4*k*x0

>	+a^4*k^2*t+x^2*t+4*t*x*x0+4*t*x0^2+2*k*t^2*x+4*k*t^2*x0+k^2*t^3)/(a^4+t^2))*cos(1/2*(-

>	2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*t+4*t*x*x0-4*t*x0^2-2*k*t^2*x+4*k*t^2*x0-k^2*t^3)/(

>	a^4+t^2))+2*exp(-a^2*(x^2+2*x*x0+2*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*

>	k^2*t+x^2*t+4*t*x*x0+4*t*x0^2+2*k*t^2*x+4*k*t^2*x0+k^2*t^3)/(a^4+t^2))*sin(1/2*(2*a^4*

>	k*x+a^4*k^2*t+2*k*t^2*x+k^2*t^3+x^2*t)/(a^4+t^2))+2*exp(-a^2*(x^2+4*x*x0+8*x0^2)/(a^4+

>	t^2))*cos(1/2*(2*a^4*k*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t

>	^2*x0+k^2*t^3)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+a^4*k^2*t+2*k*t^2*x+k^2*t^3+x^2*t)/(a^4+t

>	^2))+2*exp(-a^2*(x^2-6*x*x0+10*x0^2)/(a^4+t^2))*cos(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2

>	*t-x^2*t+4*t*x*x0-4*t*x0^2-2*k*t^2*x+4*k*t^2*x0-k^2*t^3)/(a^4+t^2))*cos(1/2*(-2*a^4*k*

>	x+8*a^4*k*x0-a^4*k^2*t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2

>	))+2*exp(-a^2*(x^2+16*x0^2)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8

>	*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t^2*x0+k^2*t^3)/(a^4+t^2))*cos(1/2*(-2*a^4*k*x+8*a^4*k

>	*x0-a^4*k^2*t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(

>	-a^2*(x^2-4*x*x0+8*x0^2)/(a^4+t^2))*cos(1/2*(2*a^4*k*x+a^4*k^2*t+2*k*t^2*x+k^2*t^3+x^2

>	*t)/(a^4+t^2))*cos(1/2*(-2*a^4*k*x+8*a^4*k*x0-a^4*k^2*t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t

>	^2*x+8*k*t^2*x0-k^2*t^3)/(a^4+t^2))-2*exp(-a^2*(x^2+16*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4

>	*k*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t^2*x0+k^2*t^3)/(a^4+

>	t^2))*sin(1/2*(-2*a^4*k*x+8*a^4*k*x0-a^4*k^2*t-x^2*t+8*t*x*x0-16*t*x0^2-2*k*t^2*x+8*k*

>	t^2*x0-k^2*t^3)/(a^4+t^2))+2*exp(-a^2*(x^2+6*x*x0+10*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4*k

>	*x+8*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t^2*x0+k^2*t^3)/(a^4+t^

>	2))*sin(1/2*(2*a^4*k*x+4*a^4*k*x0+a^4*k^2*t+x^2*t+4*t*x*x0+4*t*x0^2+2*k*t^2*x+4*k*t^2*

>	x0+k^2*t^3)/(a^4+t^2))-2*exp(-a^2*(x^2+2*x*x0+10*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4*k*x+8

>	*a^4*k*x0+a^4*k^2*t+x^2*t+8*t*x*x0+16*t*x0^2+2*k*t^2*x+8*k*t^2*x0+k^2*t^3)/(a^4+t^2))*

>	sin(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*t+4*t*x*x0-4*t*x0^2-2*k*t^2*x+4*k*t^2*x0-

>	k^2*t^3)/(a^4+t^2))-2*exp(-a^2*(x^2-2*x*x0+2*x0^2)/(a^4+t^2))*sin(1/2*(2*a^4*k*x+a^4*k

>	^2*t+2*k*t^2*x+k^2*t^3+x^2*t)/(a^4+t^2))*sin(1/2*(-2*a^4*k*x+4*a^4*k*x0-a^4*k^2*t-x^2*

>	t+4*t*x*x0-4*t*x0^2-2*k*t^2*x+4*k*t^2*x0-k^2*t^3)/(a^4+t^2))+exp(-a^2*(4*x0-x)^2/(a^4+

>	t^2))+exp(-a^2*(x+4*x0)^2/(a^4+t^2))+exp(-a^2*(x+2*x0)^2/(a^4+t^2))+exp(-a^2*(2*x0-x)^

>	2/(a^4+t^2))+exp(-a^2*x^2/(a^4+t^2)))*a^2)^(1/2);

>

>

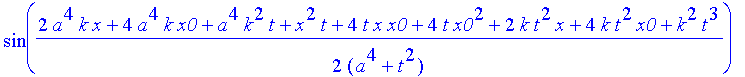
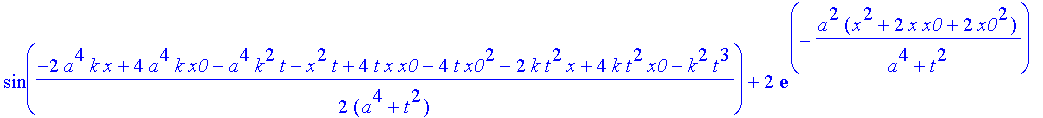
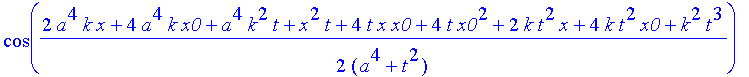
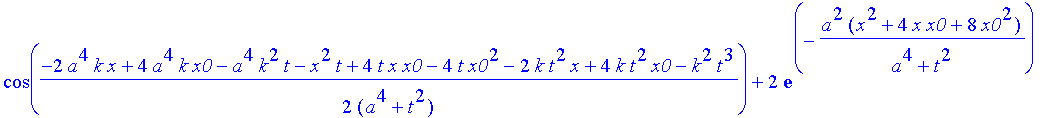
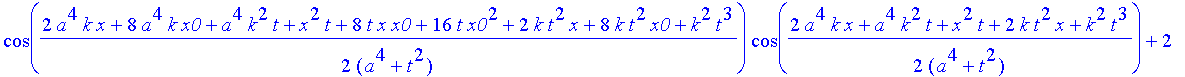
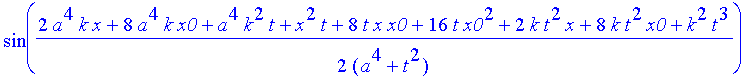
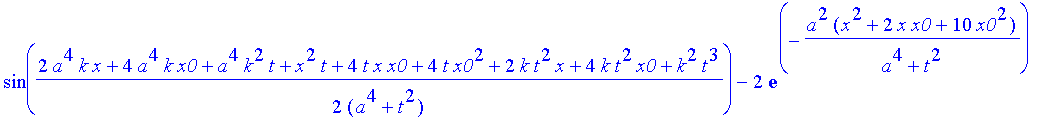
>	asumpsi:=safe3:

Man bekommt "stationäre" Zustände für x0=n*Pi/k, wobei n auch "ein geeigneter Bruch" sein darf. K kann man zweckmäßiger Weise 1/a wählen, weil Impuls und Ortsunschärfe umgekehrt proportional sind, ist dann die Ortsunschärfe gerade zur "vollen Impulsunschärfe" gewählt.

Drei Parametersätze zur Auswahl

>	#a:=2;k:=1/2;x0:=3*a; T:=2*x0/k;

>	#a:=2;k:=1/2;x0:=1.1*Pi/k;T:=2*x0/k;

>	a:=5;k:=1/a;x0:=2*Pi/k;T:=2*x0/k;

>

t:='t':

>	animate(asumpsi,x=-x0-1..x0+1,t=0..2*T,frames=20,color=red);

>

Für Abbildungen

t:=14/20*T:

plot(asumpsi,x=-x0-1..x0+1,color=red);

p2ryd:=":

Das Paket zerfließt also, aber es bildet sich durch Interferenz wieder. Zunächst an drei Stellen (Anfang=Ende), dann an zwei Stellen, zwischenzeitlich an vielen Stellen und dann wieder "in der Mitte", d.h. im Schwerpunkt .

So kann man sich die Sache auch in Ruhe anschauen:

>	plot3d(asumpsi,x=-x0-1..x0+1,t=0..4*T,style=wireframe,axes=boxed);

>

Wenn man das Amplitundenquadrat in Polarkoordinaten darstellt, wird es anschaulicher, wie das Elektron in seinem SPS vergeht und entsteht. Für einen ersten Überblick können Sie wieder den abgespeicherten Plot verwenden, also bei read `pak3.m` weitermachen. Aber dann werden Sie sicher die Parameter ändern wollen.

Elektronenpudding in Polarkoordinaten:

>	a:=5;k:=1/a;x0:=2*Pi/k;T:=2*x0/k;

>

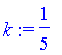
t:='t':

>	paket3:=animate([asumpsi,Pi*x/x0,x=-x0..x0],t=0..4*T,frames=80,color=red,coords=polar,scaling=constrained):

>

paket3;

>

save paket3,`pak3.m`;

>	#read `pak3.m`:

>

#paket3;

>

für Abbildungen

t:=4.1*T:

plot([asumpsi,Pi*x/x0,x=-x0..x0],color=red,coords=polar,scaling=constrained);

p9ryd:=":

save p1ryd,p2ryd,p3ryd,p4ryd, p5ryd,p6ryd,p7ryd,p8ryd,p9ryd,`abb1ryd.m`:

kürzer: save p.(1..9).ryd, filename; (nur *Namens*listen, keine arrays)

Nun transformieren wir zurück auf das Laborsystem (+- ist nur für den Umlaufsinn maßgebend, frames kann durchaus auf 200 gesetzt werden).

Man beachte im Folgenden die verschiedenen Charakteristiken und die höchst realistische Abstrahlung, d.h. den Verlust der vom Schwerpunkt zu weit abliegenden Partialwellen mit "zu hohen" und "zu niedrigen" Frequenzen.

Ggf. zuerst wieder zu read`pak4.m`

>	a:=5;k:=1/a;x0:=2*Pi/k;T:=2*x0/k;

>

t:='t':

>	paket4:=animate([asumpsi,Pi*x/x0+Pi*k*t/x0,x=-x0..x0],t=0..4*T,frames=200,color=red,coords=polar,scaling=constrained):

>

paket4;

>

save paket4,`paket4.m`;

>	#read `pak4.m`:

>

#paket4;

für Abbildungen

t:=4.1*T:

plot([asumpsi,Pi*x/x0+Pi*k*t/x0,x=-x0..x0],color=red,coords=polar,scaling=constrained);

p13ryd:=":

save p10ryd,p11ryd,p12ryd,p13ryd, `abb2ryd.m`:

>

Aber das ist alles noch nicht anschaulich genug ... ?

Wir tragen also das Absolutquadrat der "Wellenfunktion eines Elektrons auf einer Kreisbahn" über der Ebene der Kreisbahn auf. Das geht am besten in Zylinderkoordinaten.

>

t:=0:

>	plot3d([r,Pi*x/x0+Pi*k*t/x0,asumpsi],r=1..2,x=-x0..x0,coords=cylindrical,scaling=constrained,grid=[10,60]);

>

Wir wollen das Paket wieder laufen lassen, aber animate funktioniert nicht mit coords=cylindrical

#t:='t':

#animate3d([r,Pi*x/x0+Pi*k*t/x0,asumpsi],r=1..2,x=-x0..x0,t=0..4*T,frames=2,coords=cylindrical,scaling=constrained);

Also müssen wir uns eine Plotsequence selbst schreiben und bauen bei dieser Gelegenheit noch eine künstliche radiale Unschärfe ein.

Mit read`pak5.m` (übernächste Input-region) kommen Sie schneller weiter.

>	pls:='pls':

>	t:='t':N:=80:

>	pls:=seq(plot3d([r,Pi*x/x0+Pi*k*t/x0,exp(-2*(r-1.5)^2)*asumpsi],r=1..3,x=-x0..x0,coords=cylindrical,grid=[10,30]),

>	t=seq(i*4*T/N,i=0..N)):

>	paket5:=display([pls],insequence=true,orientation=[40,20]):

>

paket5;

>

save paket5,`paket5.m`;

Auf die Berechnung der (41) frames müssen Sie aber warten ...

>	#read `pak5.m`:

>

#paket5;

Es kommt ein stroboskopischer Effekt herein (je nach grid), aber so benimmt sich ein Elektron in einem hoch angeregten Zustand, und dazu gibt es auch Messungen!

>

Für Abbildungen

for i from 0 to 4 do

t:=i*T/2:

zustand[i]:=plot3d([r,Pi*x/x0+Pi*k*t/x0,exp(-2*(r-1.5)^2)*asumpsi],r=0.5..3,x=-x0..x0,coords=cylindrical,grid=[20,30],

color=black,style=hidden,orientation=[45,27]):

od:

save zustand[0],zustand[1],zustand[2],zustand[3],zustand[4], `abb3ryd.m`:

Error, save can only save names

es geht mit save nur name.(bereich), filename (keine arrays)!

for i from 0 to 4 do

z.i:=zustand[i]:od:

save z0,z1,z2,z3,z4, `abb3ryd.m`:

>