schroe_10.html

Moderne Physik mit Maple

Update auf Maple 10

Kapitel 5.3.2

Worksheet schroe_10.mws

c ITP Bonn 1995 filename: schroe.ms

Autor: Komma Datum: 27.1.94

Die Schrödingergleichung ist die Bewegungsgleichung der nicht relativistischen Quantenphysik. Gibt es Analogien zu den Bewegungsgleichungen der klassischen Physik?

Schrödingergleichung für den potentialfreien Fall (V = 0):

> restart:

> sgl:=I*h*diff(psi(x,t),t)=-h^2/(2*m)*diff(psi(x,t),x$2);

sgl := h*diff(psi(x,t),t)*I = -1/2*h^2/m*diff(psi(x,t),`$`(x,2))

>

Eine möglichst allgemein formulierte Lösung der SGL besteht aus einer reellwertigen Amplitude (Funktion von Ort und Zeit) und der Wirkungsfunktion des Systems als Phase (Notation: h statt h-quer):

> u:=A(x,t)*exp(I/h*S(x,t));

u := A(x,t)*exp(1/h*S(x,t)*I)

Was passiert, wenn wir diese Wellenfunktion in die SGL einsetzen?

> psi:=(x,t)->u;

> sgl;

h*(diff(A(x,t),t)*exp(1/h*S(x,t)*I)+A(x,t)/h*diff(S(x,t),t)*exp(1/h*S(x,t)*I)*I)*I = -1/2*h^2/m*(diff(A(x,t),`$`(x,2))*exp(1/h*S(x,t)*I)+2*I*diff(A(x,t),x)/h*diff(S(x,t),x)*exp(1/h*S(x,t)*I)+A(x,t)/h*d...

>

Umformen

> gl:=sgl/u;

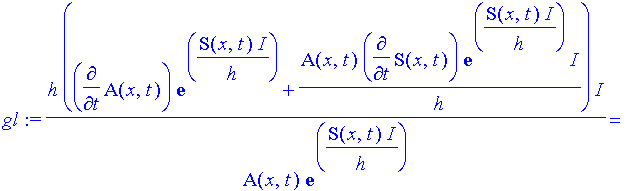
gl := 1/A(x,t)/exp(1/h*S(x,t)*I)*h*(diff(A(x,t),t)*exp(1/h*S(x,t)*I)+A(x,t)/h*diff(S(x,t),t)*exp(1/h*S(x,t)*I)*I)*I = -1/2*1/A(x,t)/exp(1/h*S(x,t)*I)*h^2/m*(diff(A(x,t),`$`(x,2))*exp(1/h*S(x,t)*I)+2*I*...

> gl:=simplify(gl);

gl := (diff(A(x,t),t)*h+A(x,t)*diff(S(x,t),t)*I)/A(x,t)*I = -1/2*(diff(A(x,t),`$`(x,2))*h^2+2*I*diff(A(x,t),x)*diff(S(x,t),x)*h+A(x,t)*diff(S(x,t),`$`(x,2))*h*I-A(x,t)*diff(S(x,t),x)^2)/A(x,t)/m

> gl:=expand(gl);

gl := 1/A(x,t)*diff(A(x,t),t)*h*I-diff(S(x,t),t) = -1/2*1/A(x,t)/m*diff(A(x,t),`$`(x,2))*h^2-I/A(x,t)/m*diff(A(x,t),x)*diff(S(x,t),x)*h-1/2*I/m*diff(S(x,t),`$`(x,2))*h+1/2*1/m*diff(S(x,t),x)^2

>

Wenn diese Gleichung erfüllt sein soll, so muß sie für den Realteil und den Imaginärteil erfüllt sein

Realteil:

> -evalc(Re(lhs(gl)))=-evalc(Re(rhs(gl)));

diff(S(x,t),t) = 1/2*1/A(x,t)/m*diff(A(x,t),`$`(x,2))*h^2-1/2*1/m*diff(S(x,t),x)^2

>

Der Gradient der Wirkungsfuktion ist der Impuls. Also steht hier die Hamilton-Jacobi-Gleichung, allerdings mit einem Zusatz, der die Dimension eines Potentials hat und mit h^2 geht. Bohm nennt ihn das Quantenpotential (das für h -> 0 verschwindet).

>

Imaginärteil:

> igl:=evalc(Im(lhs(gl)))=evalc(Im(rhs(gl)));

igl := 1/A(x,t)*diff(A(x,t),t)*h = -1/A(x,t)/m*diff(A(x,t),x)*diff(S(x,t),x)*h-1/2*1/m*diff(S(x,t),`$`(x,2))*h

> igl:=igl*A(x,t)/h;

igl := diff(A(x,t),t) = A(x,t)/h*(-1/A(x,t)/m*diff(A(x,t),x)*diff(S(x,t),x)*h-1/2*1/m*diff(S(x,t),`$`(x,2))*h)

> igl:=expand(igl);

igl := diff(A(x,t),t) = -1/m*diff(A(x,t),x)*diff(S(x,t),x)-1/2*A(x,t)/m*diff(S(x,t),`$`(x,2))

>

Das sieht nach einer Kontinuitätsgleichung aus, wenn man nämlich die Amplitude mit der Wurzel einer Teilchendichte identifiziert:

> subs(A(x,t)=sqrt(rho(x,t)),igl);

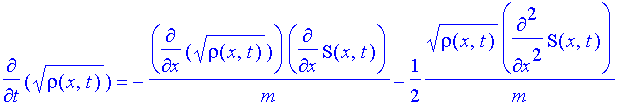
diff(rho(x,t)^(1/2),t) = -1/m*diff(rho(x,t)^(1/2),x)*diff(S(x,t),x)-1/2*rho(x,t)^(1/2)/m*diff(S(x,t),`$`(x,2))

> eval(%);

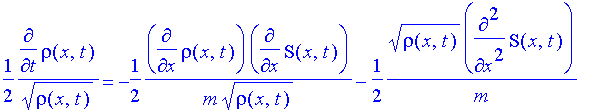
1/2*1/rho(x,t)^(1/2)*diff(rho(x,t),t) = -1/2*1/m/rho(x,t)^(1/2)*diff(rho(x,t),x)*diff(S(x,t),x)-1/2*rho(x,t)^(1/2)/m*diff(S(x,t),`$`(x,2))

> %*2*sqrt(rho(x,t));

diff(rho(x,t),t) = 2*rho(x,t)^(1/2)*(-1/2*1/m/rho(x,t)^(1/2)*diff(rho(x,t),x)*diff(S(x,t),x)-1/2*rho(x,t)^(1/2)/m*diff(S(x,t),`$`(x,2)))

> expand(%);

diff(rho(x,t),t) = -1/m*diff(rho(x,t),x)*diff(S(x,t),x)-rho(x,t)/m*diff(S(x,t),`$`(x,2))

>

Und dieser Zusammenhang führt bekanntlich auf die statistische Interpretation der Quantenmechanik.

komma@oe.uni-tuebingen.de