Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 3.3.1
Worksheet wellen4_10.mws
c International Thomson Publishing Bonn 1995 filename: wellen4.ms
Autor: Komma Datum: 5.9.94
Thema: Interferenz, Standardbeispiele in neuem Licht
[Interferenz,Spalt,Doppelspalt,Gitter, Vielstrahlinterferenz,Nahzone, Fernzone,`Auflösung`,Polarplot,`Intensitätsverteilung`],[limit,polarplot,cylinderplot],[`Superposition und Interferenz`];
Wir haben gesehen, daß Kugelwellen (Kreiswellen) die elementaren Bausteine der Wellenphysik sind. Mit ihnen läßt sich jede Wellenfront aufbauen. In diesem Worksheet werden sie dazu benützt, die Standardthemen "Doppelspalt", "Vielstrahlinterferenz" und "Spalt" zu behandeln. Wir werden diese Themen aber nicht nur pflichtgemäß abhandeln, sondern unser CAS so einsetzen, daß dabei neue Aspekte sichtbar werden.
=============
Doppelspalt
Die Phasen der beiden Wellen lassen sich so schreiben:
| > | restart:with(plots): |
| > | alpha:=k*r1-omega*t; beta:=k*r2-omega*t; |
![]()
![]()
Mit r[i] als Abstand des Aufpunktes zum Zentrum 1 bzw. 2. Wenn wir sinusförmige Wellen ansetzen (die in der Fernzone nicht merklich abklingen), dann können wir die Summe der beiden Wellen auch als Produkt schreiben, wobei der Faktor "am" für die ortsabhängige Amplitude steht und der Faktor "pha" für die Phasenfunktion.
| > | am:=2*cos((alpha-beta)/2); pha:=sin((alpha+beta)/2); |
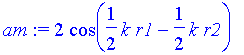
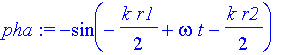
Zentren bei x1 und x2 auf der x-Achse:
| > | r1:=sqrt((x-x1)^2+y^2); r2:=sqrt((x-x2)^2+y^2); |
![]()
![]()
Zahlenbeispiel:
| > | k:=2*Pi/4: x1:=5: x2:=-5: |
Amplitudenquadrat
| > | plot3d(am^2,x=-20..20,y=-20..20,axes=boxed,orientation=[40,7],numpoints=1000); |
![[Maple Plot]](wellen4/wellen4_107.gif)
| > |
| > |
Es entstehen also die bekannten Interferenzhyperbeln k*(r1-r2)=const
Ebenso können wir die Kurven gleicher Phase darstellen, also die Wellenfronten k*(r1+r2)=const. Das ist die zur Hyperbelschar orthogonale Ellipsenschar:
| > | t:=0: |
| > | plot3d(pha,x=-10..10,y=-10..10,axes=boxed,orientation=[40,7],numpoints=1000); |
![[Maple Plot]](wellen4/wellen4_108.gif)
| > |
Mit geeigneter Orientierung des Plots kann man sich viel Rechenzeit sparen und bekommt vor allem besseren Einblick in die Täler.
Demonstration der Orthogonalität
| > | cp1:=contourplot(am^2,x=-20..20,y=-20..20,axes=boxed,numpoints=5000, |
| > | scaling=constrained,contours=4,color=black): |
| > | t:=0: |
| > | cp2:=contourplot(pha,x=-20..20,y=-20..20,axes=boxed,numpoints=5000, |
| > | scaling=constrained,contours=4,color=red): |
| > | cp1;cp2; |
![[Maple Plot]](wellen4/wellen4_109.gif)
![[Maple Plot]](wellen4/wellen4_1010.gif)
| > |
| > | display({cp1,cp2});#,orientation=[-90,0]); |
![[Maple Plot]](wellen4/wellen4_1011.gif)
Wenn die Interferenzhyperbeln nicht wären, würde von den beiden Zentren aus eine elliptische Welle mit richtungsunabhängiger Amplitude laufen.
| > | t:='t': omega:=2: n:=20: |
| > | animate3d(pha,x=-10..10,y=-10..10,t=0..2*Pi/omega*(1-1/n),axes=boxed,orientation=[40,7], |
| > | style=hidden,color=blue,frames=n); |
![[Maple Plot]](wellen4/wellen4_1012.gif)
Aber wir müssen ja das Produkt bilden:
| > | t:=0: |
| > | plot3d(am*pha,x=-10..10,y=-10..10,axes=boxed,orientation=[40,7]); |
![[Maple Plot]](wellen4/wellen4_1013.gif)
| > | #plot3d({am,pha+20},x=-5..5,y=-5..5,axes=boxed,orientation=[40,45],numpoints=1000); |
Wo liegen die Minima?
In der Bewegung sieht man sie besser:
| > | t:='t': # omega:=2: n:=20: x1:=5: x2:=-5: |
| > | animate3d(am*pha,x=-10..10,y=-10..10,t=0..2*Pi/omega*(1-1/n),axes=boxed,orientation=[40,7], |
| > | style=hidden,color=blue,frames=n); |
![[Maple Plot]](wellen4/wellen4_1014.gif)
... wenn man sich etwas Mühe gibt. Man kann sich die Suche erleichtern, wenn man den Amplitudenfaktor einblendet:
| > | animate3d({am*pha,am},x=-10..10,y=-10..10,t=0..2*Pi/omega*(1-1/n),axes=boxed,orientation=[40,7], |
| > | style=hidden,color=blue,frames=n); |
![[Maple Plot]](wellen4/wellen4_1015.gif)
Untersuchen Sie: Was ändert sich mit x1, x2, k, omega?
| > |
| > |
Vielstrahlinterferenz
Auf der x-Achse seien n Zentren äquidistant mit der Gitterkonstanten g angeordnet. Im Abstand b zur x-Achse soll die Intensitätsverteilung längs einer zur x-Achse parallelen Geraden bestimmt werden.
Neben der Erhöhung der Zahl der Zentren gibt es noch die zwei Aspekte "Nahzone" und "Fernzone". Wir beschäftigen uns zunächst mit der Intensitätsverteilung in der Nahzone (was nicht heißt, daß b im Folgenden nicht beliebig groß gewählt werden kann).
| > |
| > | restart:with(plots): |
| > | rj:=sqrt((x-xj)^2+b^2); |
![]()
| > | xj:=g*j-(n+1)/2*g; |
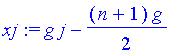
| > | phj:=k*rj; |
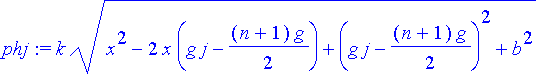
| > | n:='n': |
| > | #Ac:=(sum(cos(phj),j=1..n))^2; |
| > | A:=sum(exp(I*phj),j=1..n); |
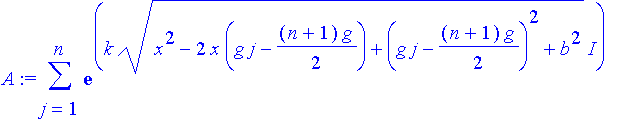
(Anm.1: Die Summe muß nicht mit indizierten Variablen gebildet werden. Anm.2: Wenn man nur Cosinuswellen aufsummiert, bekommt man nicht das zeitunabhängige Amplitudenquadrat)
| > | k:=2*Pi/lambda; |
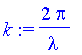
n-loop:
| > | n:=4: # muss vor evalc stehen, und evalc wird fuer plot benoetigt |
| > | g:='g': lambda:='lambda': b:='b': |
| > | intens:=evalc(abs(A))^2: |
| > | #reint:=evalc(Re(A)):# vergl. Anm. zu Cosinuswellen |
| > | #A;intens; |
Parameter-loop
| > | b:=5: lambda:=2: g:=5:# b:=0 zur Kontrolle |
| > | plot(intens,x=-15..15); |
![[Maple Plot]](wellen4/wellen4_1021.gif)
Wenn Sie mit den Parametern und der Zahl der Zentren spielen, werden Sie einige Überraschungen erleben ...
Wie anders als mit einem CAS könnte man mit dieser Geschwindigkeit und dieser Präzision die Antwort auf solche Fragen erhalten?
| > | #plot(reint,x=0..300); # Cosinuswellen |
Aber mit der Intensitätsverteilung längs einer Geraden sind die Möglichkeiten von Maple natürlich nicht erschöpft.
Richtungsverteilungen sind fast noch informativer. Man beachte die Änderung der Strahlungscharakteristik mit r!
Wie ändert sich also die Intensität, wenn man auf einem Kreis mit Radius r um die Zentren herumläuft?
| > | restart:with(plots): |
Abstand zum Zentrum rj
| > | rj:=sqrt((r*cos(phi)-xj)^2+(r*sin(phi))^2); |
![]()
Position der Zentren, zugehörige Phase
| > | xj:=g*j-(n+1)/2*g; |
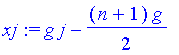
| > | phj:=k*rj; |
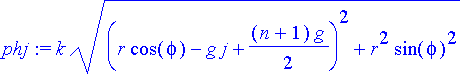
Summe der Amplituden
| > | n:='n': |
| > | A:=sum(exp(I*phj),j=1..n); |
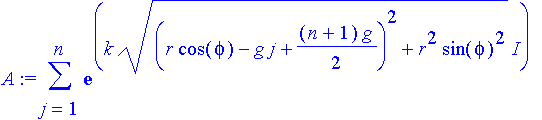
| > | k:=2*Pi/lambda; |
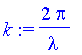
n-loop:
| > | n:=4: g:='g':lambda:='lambda':r:='r': |
| > | intens:=evalc(abs(A))^2: |
| > | #reint:=evalc(Re(A)): |
Parameter-loop:
| > | g:=5: lambda:=4: |
r-loop:
| > | r:=8: # Octopussy? |
| > | polarplot(intens,scaling=constrained); |
![[Maple Plot]](wellen4/wellen4_1027.gif)
| > | #r:='r': |
| > | #plot3d([r*cos(phi),r*sin(phi),intens],r=0..30,phi=0..2*Pi,axes=boxed,grid=[20,100]); |
Und für den totalen Überblick kann man die Richtungsverteilungen in einem Zylinderplot übereinander schichten.
| > | r:='r': #Nautilus! |
| > | cylinderplot(intens,phi=0..Pi,r=0.1..4,axes=boxed,grid=[100,10],style=hidden); |
![[Maple Plot]](wellen4/wellen4_1028.gif)
(Nach r = 4 geht es noch weiter und weiter und ...)
| > |
Übergang zur Fernzone.
Wir betrachten nach wie vor punktförmige Zentren oder Öffnungen. Ihre Anzahl sei p. In der Fernzone haben wir parallele Strahlen, was die Berechnung der Intensitätsverteilung stark vereinfacht. Je zwei benachbarte Strahlen haben die gleiche Phasendifferenz d, die in den Plots als unabhängige Variable dient.
| > | restart:with(plots): |
| > | A:=sum(exp(I*k*d),k=0..p-1); |
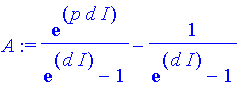
Die Summe kann in diesem Fall (im Gegensatz zur Nahzone) kompakt dargestellt werden und Maple macht das auch (geometrische Reihe):
| > | A:=simplify(A); |
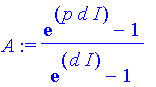
Ein erfreuliches Ergebnis. Wie sieht es aus?
| > | p:='p': |
| > | intensg:=evalc(abs(A))^2: |
| > | #rea:=evalc(Re(A)): |
| > | p:=5: |
| > | plot(intensg,d=-10..10); |
![[Maple Plot]](wellen4/wellen4_1031.gif)
| > |
Wie ändert sich die Intensitätsverteilung mit der Anzahl p der Strahlen?
| > | p:='p': |
| > | plot({seq(intensg/p, p=2..6)},d=-10..10); |
![[Maple Plot]](wellen4/wellen4_1032.gif)
| > |
Einzelspalt endlicher Breite (= oo viele Zentren auf endlichem Raum)
Die Intensitätsverteilung am Einzelspalt erhält man nun, wenn man auf der Spaltbreite b, eine wachsende Anzahl p von Strahlenbündeln endlicher Breite beta=b/p unterbringt. Sinnvollerweise gibt man diesen Strahlenbündeln die Amplitude beta. Mit der Phasendifferenz Delta der Randstrahlen, bzw. delta = Delta/p für benachbarte Strahlenbündel, kann die Intensitätsverteilung durch Aufsummieren der Amplituden der parallelen Strahlen bestimmt werden, wenn man den Grenzwert für p gegen Unendlich bildet.
| > | b:='b':p:='p':Delta:='Delta':delta:='delta': |
| > | beta:=b/p; |
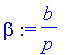
| > | delta:=Delta/p; |
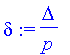
| > | As:=beta*sum(exp(I*k*delta),k=0..p-1); |
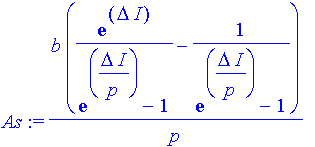
| > | simplify(As); |
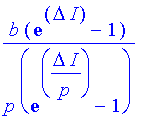
Grenzwert
| > | Asl:=limit(As,p=infinity); |
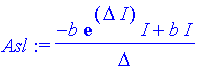
Betragsquadrat
| > | Asq:=evalc(abs(Asl))^2; |
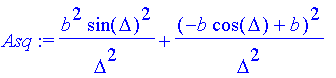
| > | Asq:=simplify(Asq); |
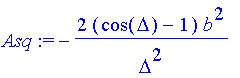
Also Minima für eine Phasendifferenz Delta=k*2*Pi oder einen Gangunterschied von k*lambda für die Randstrahlen. Eine gängigere Version ist (Mit Delta = 2*Pi*b/lambda*sin(phi). Es ist aber für das Folgende bequemer Delta beizubehalten):
| > | Asd:=subs(cos(Delta)-1=-2*sin(Delta/2)^2,Asq); |
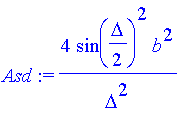
| > | b:=10: Delta:='Delta': |
| > | plot(Asd,Delta=-15..15); |
![[Maple Plot]](wellen4/wellen4_1041.gif)
| > |
Schließlich können wir die Strahlenbündel aus p Einzelspalten zur Interferenz bringen (p hat jetzt wieder die gleiche Bedeutung wie beim Gitter). Die Öffnungen seien mit der Gitterkonstanten g angeordnet. Von oben haben wir noch die Intensitätsverteilung "intensg" für punktförmige Öffnungen zur Verfügung, die wir nur mit der Intensitätsverteilung des Einzelspaltes multiplizieren müssen. Es gibt zwei Möglichkeiten der Darstellung:
1.) Unabhängige Variable ist die Phasendifferenz d der Zentralstrahlen zweier Öffnungen. Dann gilt für Delta (Strahlensatz):
| > | d:='d': b:='b':g:='g': |
| > | Delta:=b*d/g; |
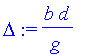
| > | b:=2: g:=4: p:=4: |
| > | plot({Asd/b,Asd*intensg/b/p^2},d=-30..30,numpoints=500); |
![[Maple Plot]](wellen4/wellen4_1043.gif)
| > | plot({Asd/b,Asd*intensg/b/p^2,intensg/p^2},d=-30..30,numpoints=500); # Einblenden der "Gitteverteilung" |
![[Maple Plot]](wellen4/wellen4_1044.gif)
| > |
Was geschieht, wenn man die Breite der Öffnungen ändert?
Simulation der simultanen Änderung der Breite der p Öffnungen (default: frames=16)
| > | b:='b': |
| > | animate({Asd/b,Asd*intensg/b/p^2},d=-100..100,b=g/10..g,numpoints=500); |
![[Maple Plot]](wellen4/wellen4_1045.gif)
| > |
===================================
Aufgabe: Polarplot der Intensitätsverteilung.
| > | lambda:='lambda':b:='b': p:='p':g:='g': |
| > | d:=2*Pi/lambda*g*sin(phi); |
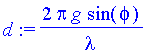
| > | #Asd;intensg;Delta; |
| > | lambda:=5:g:=11: b:=3:p:=2: |
| > | polarplot(Asd*intensg/b/p^2,phi=0..2*Pi,numpoints=500,scaling=constrained); |
![[Maple Plot]](wellen4/wellen4_1047.gif)
Zur Animation wird mit 1/b^2 normiert, um die Amplitude konstant zu halten. (Bitte warten)
| > | b:='b': |
| > | animate({[Asd*intensg/b^2/p^2,phi,phi=0..2*Pi], |
| > | [Asd/b^2,phi,phi=0..2*Pi]}, |
| > | b=g/10..g,numpoints=200,scaling=constrained,coords=polar); |
![[Maple Plot]](wellen4/wellen4_1048.gif)
| > |
| > |
| > |
2.) Zweite Möglichkeit der Darstellung. Unabhängige Variable ist Delta
| > | b:='b':g:='g':Delta:='Delta': |
| > | d:=Delta*g/b; |
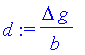
| > | b:=2: g:=4: p:=2: |
| > | plot({Asd/b,Asd*intensg/b/p^2},Delta=-15..15,numpoints=200); |
![[Maple Plot]](wellen4/wellen4_1050.gif)
| > |
Simulation der simultanen Änderung der Abstände der p Öffnungen
| > | g:='g': |
| > | animate({Asd/b,Asd*intensg/b/p^2},Delta=-15..15,g=b..10*b,numpoints=500); |
![[Maple Plot]](wellen4/wellen4_1051.gif)
| > |
In Polarkoordinaten:
| > | lambda:='lambda':b:='b': p:='p':g:='g': |
| > | Delta:=2*Pi/lambda*b*sin(phi); |

| > | lambda:=5:g:=11: b:=3:p:=2: |
| > | polarplot(Asd*intensg/b/p^2,phi=0..2*Pi,numpoints=500,scaling=constrained); |
![[Maple Plot]](wellen4/wellen4_1053.gif)
| > |
Animation (Bitte warten)
| > | g:='g': |
| > | animate({[Asd*intensg/b^2/p^2,phi,phi=0..2*Pi], |
| > | [Asd/b^2,phi,phi=0..2*Pi]}, |
| > | g=b..b*10,numpoints=200,scaling=constrained,coords=polar); |
![[Maple Plot]](wellen4/wellen4_1054.gif)
| > |
Und das Schirmbild auf dem Bildschirm
##### Densityplot in R5 und Maple 6 nicht mehr zu gebrauchen......
| > | g:=15: |
#densityplot((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[1000,2],style=patchnogrid,scaling=constrained);
| > | plot3d((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,y=0..1,axes=none,grid=[1000,2],style=patchnogrid,orientation=[90,0],shading=ZGREYSCALE); |
![[Maple Plot]](wellen4/wellen4_1055.gif)
| > |
| > | #plot((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,style=patchnogrid,scaling=constrained); |
| > |
### Release 5 vertauscht Achsen
#densityplot((Asd*intensg/b/p^2),etwas=0..5,phi=-Pi/2..Pi/2,grid=[30,3],style=patchnogrid,scaling=constrained);
#densityplot((Asd*intensg/b/p^2),y=0..1,phi=-Pi/2..Pi/2,axes=none,grid=[200,2],style=patchnogrid,scaling=constrained);
#densityplot((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[1000,2],style=patchnogrid,
colorstyle=HUE);
| > |
Aber bitte in Farbe!
| > |
| > | plot3d((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[1000,2],style=patchnogrid,shading=ZHUE,orientation=[90,0]); |
![[Maple Plot]](wellen4/wellen4_1056.gif)
| > |
| > | #plot3d(ln(Asd*intensg/b/p^2+1),phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[1000,2],style=patchnogrid,color=phi); |
| > |
Kann man auch eine realistische Einfärbung erreichen?
Im density-Plot nicht. Also Rückgriff auf plot3d:
| > |
| > | lambda:=5: |
| > | rot:=plot3d((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[500,2],style=patchnogrid,color=[Asd*intensg/b/p^2,0,0],orientation=[90,0]): rot; |
![[Maple Plot]](wellen4/wellen4_1057.gif)
| > |
| > | lambda:=3: |
| > | blau:=plot3d((Asd*intensg/b/p^2),phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[500,2],style=patchnogrid, |
| > | color=[0,0,Asd*intensg/b/p^2],orientation=[90,0]): blau; |
![[Maple Plot]](wellen4/wellen4_1058.gif)
| > | display({rot,blau}); |
![[Maple Plot]](wellen4/wellen4_1059.gif)
| > |
| > | lambda:='lambda': |
| > | #Asd;intensg; |
| > | licht:=Asd*intensg/b/p^2; |
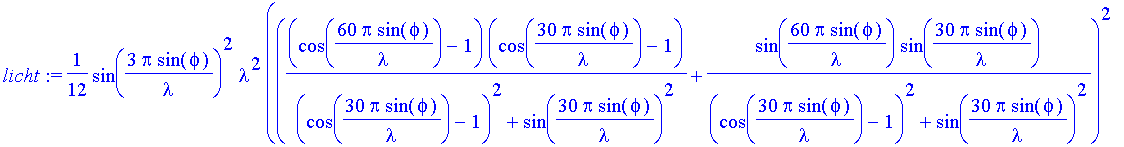
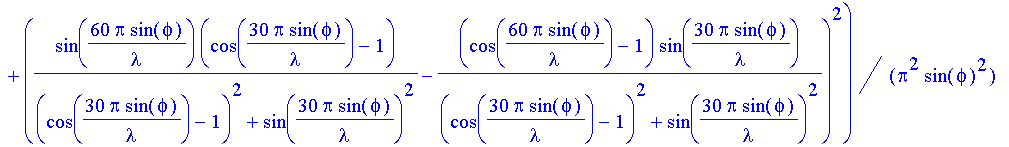
| > | lrot:='lrot': lblau:='lblau': |
| > | rotlicht:=subs(lambda=lrot,licht); |
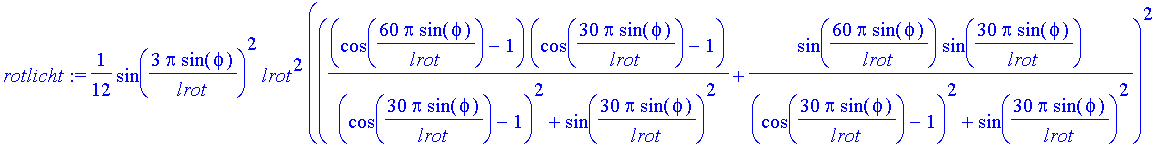
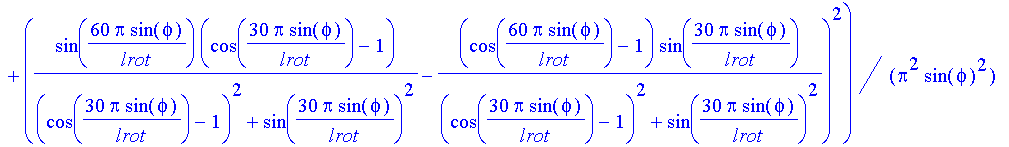
| > | blaulicht:=subs(lambda=lblau,licht); |
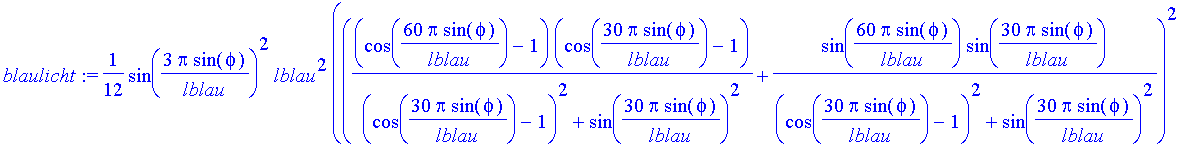
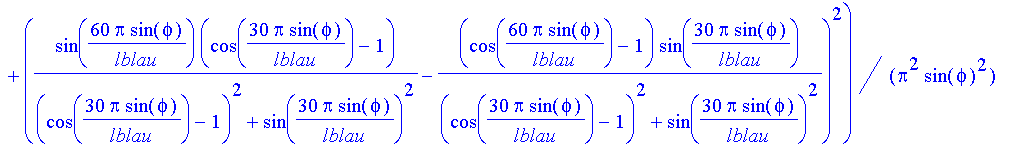
| > | lrot:=5: lblau:=3: |
| > | plot3d(rotlicht+blaulicht,phi=-Pi/2..Pi/2,y=0..0.25,axes=none,grid=[500,2],style=patchnogrid, |
| > | color=[rotlicht,0,blaulicht],orientation=[90,0]); |
![[Maple Plot]](wellen4/wellen4_1066.gif)
| > |
komma@oe.uni-tuebingen.de