Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 4.1.3
Worksheet wirf5_10.mws
c International Thomson Publishing Bonn 1995 filename: wirf5.ms
Autor: Komma Datum: 28.3.94
Thema: Approximation durch stückw. gleichf. Bewegung, Wirkungsprinzip.
Weiterentwicklung von wirf4.ms mit procs()
| > | restart; with(plots): |
| > | Lq:=Tq-Vq(); # Vq() wird als proc formuliert, damit die Änderungen aller Parameter weitergereicht werden |
| > | clear:= proc(x) local p; |
| > | for p to n do |
| > | x[p]:=evaln(x[p]); od; end; |
![clear := proc (x) local p; for p to n do x[p] := evaln(x[p]) end do end proc](wirf5/wirf5_102.gif){kind=small}
| > |
| > | n:='n': dt:='dt':x[0]:='x[0]': |
| > | Tq:=m/(2*dt)*sum((x[j]-x[j+1])^2,j=0..n-1); |
![Tq := 1/2*m/dt*sum((x[j]-x[j+1])^2,j = 0 .. n-1)](wirf5/wirf5_103.gif)
| > | m:='m':g:='g':k:='k':x[0]:='x[0]': |
| > | V:=proc(x) |
| > | 1/2*k*x^2; |
| > | #m*g*x; |
| > | end; |
| > | if assigned(n) then clear(x) fi; |
| > | n:='n': dt:='dt': |
| > |
| > | Vq:=proc() dt*sum(V(x[j]),j=0..n-1); |
| > | end; |
![Vq := proc () dt*sum(V(x[j]),j = 0 .. n-1) end proc](wirf5/wirf5_105.gif){kind=small}
| > | #n:=20: |
| > | #bahn(); |
| > | Lq; |
![1/2*m/dt*sum((x[j]-x[j+1])^2,j = 0 .. n-1)-dt*sum(1/2*k*x[j]^2,j = 0 .. n-1)](wirf5/wirf5_106.gif)
| > | bahn:=proc() local kk,j,i; global sys,sol,pkte; |
| > | if assigned(n) then clear(x) fi; |
| > |
| > | sys:=seq(diff(Lq,x[kk])=0,kk=1..n-1); |
| > | sol:=solve({sys},{seq(x[j],j=1..n-1)}): |
| > | assign(sol); |
| > | pkte:=array(1..n): |
| > | for i to n do |
| > | pkte[i]:=x[i] : |
| > | od: |
| > | end; |
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_107.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_108.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_109.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1010.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1011.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1012.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1013.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1014.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1015.gif){kind=small}
![bahn := proc () local kk, j, i; global sys, sol, pkte; if assigned(n) then clear(x) end if; sys := seq(diff(Lq,x[kk]) = 0,kk = 1 .. n-1); sol := solve({sys},{seq(x[j],j = 1 .. n-1)}); assign(sol); pkte...](wirf5/wirf5_1016.gif){kind=small}
| > |
Tests
| > | n:=10;bahn(); |
![x[10]](wirf5/wirf5_1018.gif){kind=small}
Etwas Computeralgebra
| > | x[3]; |
![m^3*(55*m^2*dt^8*k^4*x[0]-120*m^3*dt^6*k^3*x[0]-12*m*dt^10*k^5*x[0]+dt^12*k^6*x[0]-4*m^5*dt^2*k*x[10]+m^4*dt^4*k^2*x[10]-56*m^5*dt^2*k*x[0]+126*dt^4*k^2*m^4*x[0]+7*m^6*x[0]+3*m^6*x[10])/(-dt^18*k^9+792...](wirf5/wirf5_1019.gif){kind=small}
![m^3*(55*m^2*dt^8*k^4*x[0]-120*m^3*dt^6*k^3*x[0]-12*m*dt^10*k^5*x[0]+dt^12*k^6*x[0]-4*m^5*dt^2*k*x[10]+m^4*dt^4*k^2*x[10]-56*m^5*dt^2*k*x[0]+126*dt^4*k^2*m^4*x[0]+7*m^6*x[0]+3*m^6*x[10])/(-dt^18*k^9+792...](wirf5/wirf5_1020.gif){kind=small}
![m^3*(55*m^2*dt^8*k^4*x[0]-120*m^3*dt^6*k^3*x[0]-12*m*dt^10*k^5*x[0]+dt^12*k^6*x[0]-4*m^5*dt^2*k*x[10]+m^4*dt^4*k^2*x[10]-56*m^5*dt^2*k*x[0]+126*dt^4*k^2*m^4*x[0]+7*m^6*x[0]+3*m^6*x[10])/(-dt^18*k^9+792...](wirf5/wirf5_1021.gif){kind=small}
| > | collect(x[3],x[0]); |
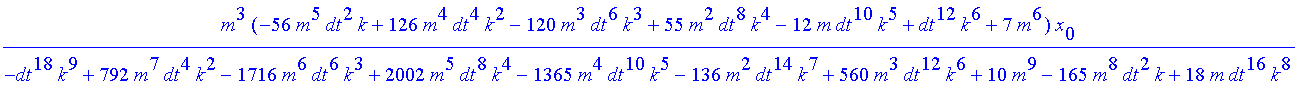
| > | factor(x[3]); |
![m^3*(55*m^2*dt^8*k^4*x[0]-120*m^3*dt^6*k^3*x[0]-12*m*dt^10*k^5*x[0]+dt^12*k^6*x[0]-4*m^5*dt^2*k*x[10]+m^4*dt^4*k^2*x[10]-56*m^5*dt^2*k*x[0]+126*dt^4*k^2*m^4*x[0]+7*m^6*x[0]+3*m^6*x[10])/(2*m-k*dt^2)/(m...](wirf5/wirf5_1024.gif){kind=small}
![m^3*(55*m^2*dt^8*k^4*x[0]-120*m^3*dt^6*k^3*x[0]-12*m*dt^10*k^5*x[0]+dt^12*k^6*x[0]-4*m^5*dt^2*k*x[10]+m^4*dt^4*k^2*x[10]-56*m^5*dt^2*k*x[0]+126*dt^4*k^2*m^4*x[0]+7*m^6*x[0]+3*m^6*x[10])/(2*m-k*dt^2)/(m...](wirf5/wirf5_1025.gif){kind=small}
![m^3*(55*m^2*dt^8*k^4*x[0]-120*m^3*dt^6*k^3*x[0]-12*m*dt^10*k^5*x[0]+dt^12*k^6*x[0]-4*m^5*dt^2*k*x[10]+m^4*dt^4*k^2*x[10]-56*m^5*dt^2*k*x[0]+126*dt^4*k^2*m^4*x[0]+7*m^6*x[0]+3*m^6*x[10])/(2*m-k*dt^2)/(m...](wirf5/wirf5_1026.gif){kind=small}
| > |
Parameter
Die Anzahl der Stützstellen kann noch mit t1 abgestimmt werden, insbes. für die Schwingung (z.B. n=20*t1). (Rundungsfehler?)
| > | n:=40: |
| > | m:=1: |
| > | k:=6: |
| > | #g:=50: |
| > | t1:=3: # untersuchen Sie auch größere Zeiten |
| > | dt:=t1/n: |
| > | x[0]:=1: # nicht 0 |
| > | bahn(); |
![x[40]](wirf5/wirf5_1027.gif){kind=small}
| > | x[n]:=0: |
| > |
| > | x[5]; |
| > |
| > | plota:=plot([[0,x[0]],seq([i*dt,pkte[i]],i=1..n-1),[n*dt,x[n]]]): |
| > | plota; |
![[Maple Plot]](wirf5/wirf5_1029.gif)
| > |
| > | ITq:=evalf(Tq); IVq:=evalf(Vq()); Sq:=evalf(Lq); |
| > |
| > | soly:=proc() local F; F:=-diff(V(y),y): |
| > | rhs(dsolve({diff(y(t),t$2)=subs(y=y(t),F)/m,y(0)=x[0],y(t1)=x[n]},y(t))); end; |
![soly := proc () local F; F := -diff(V(y),y); rhs(dsolve({y(0) = x[0], y(t1) = x[n], diff(y(t),`$`(t,2)) = subs(y = y(t),F)/m},y(t))) end proc](wirf5/wirf5_1033.gif){kind=small}
| > | soly(); |
| > |
| > | plote:=plot(soly(),t=0..t1,color=black):#plote; |
| > | display({plota,plote}); |
![[Maple Plot]](wirf5/wirf5_1035.gif)
| > |
| > | IT:=evalf(int(m/2*diff(soly(),t)^2,t=0..t1)); |
| > | IV:=evalf(int(V(soly()),t=0..t1)); |
| > | S:=IT-IV; |
| > |
Zurück zu "Parameter" ... Sie können alle ändern! Unter welchen Bedingungen wird die Näherung schlecht?
Wie läßt sich die Näherung verfeinern?
| > |
komma@oe.uni-tuebingen.de