![[Maple Plot]](wiwurf1/wiwurf1_101.gif)
Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 5.2.1
Worksheet wiwurf1_10.mws
c International Thomson Publishing 1995 filename: wiwurf1
Autor: Komma Datum: Oktober 94
Thema: Wirkungswellen beim Wurf, Orthogonaltrajektorien
Wellenfronten des schiefen Wurfes
Trajektorien
In der Physik benötigt man oft die Gleichung und Darstellung einer Kurvenschar, deren Kurven mit den Kurven einer gegebenen Schar einen bestimmten Winkel bilden (Feld -- Potential, Wellenfront -- Strahl, ...). Diese Aufgabe läßt sich leicht bewerkstelligen, wenn man die DG (1.Ordnung) der gegebenen Schar hat. Zu der Schar mit y'=f(x) lautet die DG der Trajektorien: yt'=(1+cf)/(c-f) , mit c als Cotangens des eingeschlossenen Winkels.
Dieses Worksheet ist als Anhang zu wiwurf.ms gedacht. Die Wellenfronten werden als Orthogonaltrajektorien der Bahnen berechnet, quasi als Übung in Differentialgeometrie (vgl. Anhang). Natürlich fehlt diesem Vorgehen die Eleganz des Wirkungsprinzips, das die Wellen automatisch liefert.
| > | restart; with(DEtools):with(plots): |
DG der Bahnen in allgemeiner Form dgl:=diff(y(x),x)=f;
DG der O-Traj. (c=0 kommt später)
| > | dgt:=diff(y(x),x)=(1+c*f)/(c-f): |
Bereitstellen der Parabelschar für den Plot
| > | parpl:=plot({seq(5-(x-a)^2,a=-3..3)},x=-5..5,-5..5): |
| > | parpl; |
![[Maple Plot]](wiwurf1/wiwurf1_101.gif)
Als Gleichung
| > | a:='a': |
| > | par:=y(x)=5-(x-a)^2; |
![]()
Eliminieren des Scharparameters durch Auflösen nach a
| > | asol:=solve(par,a); |
![]()
und Differenzieren
| > | dgl:=subs(a=asol[1],diff(par,x)); |
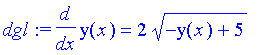
Also ist die rechte Seite der DG 1.Ordng.
| > | f:=solve(dgl,diff(y(x),x)); |
![]()
Und die DG der O-Traj. kann gelöst werden
| > | c:=0: |
| > | sol:=[dsolve(dgt,y(x),explicit)]; |
![sol := [y(x) = RootOf(3*x-4*(-_Z+5)^(3/2)+3*_C1)]](wiwurf1/wiwurf1_106.gif)
| > | allvalues(sol); |
![[y(x) = 5-1/4*(6*x+6*_C1)^(2/3)], [y(x) = 5-(-1/4*(6*x+6*_C1)^(1/3)+1/4*I*3^(1/2)*(6*x+6*_C1)^(1/3))^2], [y(x) = 5-(-1/4*(6*x+6*_C1)^(1/3)-1/4*I*3^(1/2)*(6*x+6*_C1)^(1/3))^2]](wiwurf1/wiwurf1_107.gif)
| > |
| > | solt:=rhs(sol[1]); ############ Vorsicht: mit Index reelle Lösung wählen! |
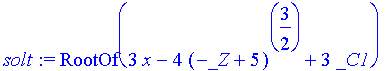
| > | ############ Die Nummer der Integrationskonstanten beachten! |
| > |
| > | ## lange Rechenzeit in R6 |
| > | ptra:=plot({seq(solt,_C1=seq(i,i=-5..5))},x=-5..5,color=black,scaling=constrained): |
| > | ptra; |
![[Maple Plot]](wiwurf1/wiwurf1_109.gif)
| > | display({ptra,parpl}); |
![[Maple Plot]](wiwurf1/wiwurf1_1010.gif)
Es gibt auch noch Richtungsfelder ...
| > |
| > |
| > | # läuft in R6 wieder!! y=0.1... |
| > | dfieldplot(dgt,y(x),x=0..5,y=0.1..5); |
![[Maple Plot]](wiwurf1/wiwurf1_1011.gif)
| > | #dgt; |
| > |
| > | display({dfieldplot(dgt,y(x),x=0..5,y=0.1..5),dfieldplot(dgl,y(x),x=0..5,y=0.1..5),ptra},view=[0..5,0..5]); |
![[Maple Plot]](wiwurf1/wiwurf1_1012.gif)
| > | #dgl; |
| > |
Die charakteristische Funktion erhält man durch die Fragestellung: "Für welche (x|y) ist solt konstant?" Die Antwort lautet:
| > | _C1:='_C1': |
| > | s1:=allvalues(solt)[1]; |
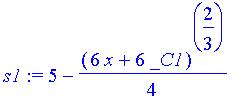
| > | w:=solve(y=s1,_C1); |
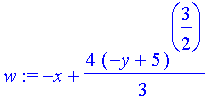
Die Wirkungswellen sehen als so aus:
| > | plot3d(evalc(Re(exp(I*w))),x=-10..10,y=0..7,axes=boxed,numpoints=2000,orientation=[-75,10]); |
![[Maple Plot]](wiwurf1/wiwurf1_1015.gif)
Und bewegen sich so:
| > | H:=1: |
| > | animate3d(evalc(Re(exp(I*(w-H*t)))),x=-10..10,y=0..7,t=0..2*Pi,axes=boxed,numpoints=2000, |
| > | style=wireframe,frames=20,orientation=[-75,10],style=patchcontour); |
![[Maple Plot]](wiwurf1/wiwurf1_1016.gif)
| > |
komma@oe.uni-tuebingen.de