HOME | Projekte | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top
"Aktualisierung" Oktober 2017: Nach 20 Jahren reden heute wieder viele von der "Digitalisierung". Dabei war vor 20 Jahren eigentlich schon klar:
"Die neuen Technologien sind kein von der Gesellschaft isoliertes Phänomen, das ‘über uns kam’. Wir haben es produziert, wir müssen damit fertig werden" (s.u.). Übrigens: auch in BW reift nun wieder die Erkenntnis, dass man wieder Leistungskurse einführen sollte...
Das Mobile Klassenzimmer
am Isolde-Kurz-Gymnasium Reutlingen
Dr. M. Komma
Februar 1998
Gekürzte Web-Fassung des Arbeitsexemplars
Die gekürzte Fassung des Abschlußberichts (mit Abitur) gibt es hier.
Lieber Leser im Web. Das Kleingedruckte ist oft wichtiger als die fette Überschrift, denn es gibt Auskunft über die Hintergründe. Ich habe lange gezögert, unsere Arbeit im 'Mobilen Klassenzimmer' im Web zusammenfassend zu beschreiben, weil wir einfach noch nicht so weit sind, eine druckreife Fassung präsentieren zu können. Da unsere Arbeit aber auch darin besteht, im Web zu kommunizieren, konnten und wollten wir sie nicht länger geheim halten. Wir bitten nur um Verständnis, wenn wir nun (Juli 98) ein Manuskript (Februar 98) zur Verfügung stellen statt einer perfekt verlinkten Ausgabe. Der Druck durch die vielen Nachfragen war einfach zu groß.
Mitwirkende, Berater und Förderer *
OSD H. Öttinger, MR Stroman, Initiatoren und Wegbereiter des Projekts
Ministerium für Kultus und Sport Baden-Württemberg:
OSR W. Kinkelin, Projektleitung
Oberschulamt Tübingen:
RSD Selinka, CAS-Fortbildungen
Isolde-Kurz-Gymnasium:
OSD Dr. W. Borth, Schulleiter
Die Schüler des Mobilen Klassenzimmers.
Besonders verantwortungsvolle und arbeitsintensive Aufgaben übernahmen:
Fabian Hust (LK Mobiles Klassenzimmer): Webmaster des virtuellen Klassenzimmers
Michael Bayer (LK Mobiles Klassenzimmer): Betreuung des Mail-Servers
Tim Schorer (LK Mobiles Klassenzimmer): Betreuung des lokalen Netzes
Daniel Weihing (LK Mobiles Klassenzimmer): Betreuung des Dominoservers
Ralph Jäger und Thomas Altmann (Abitur 1996): Aufbau und Betreuung des lokalen Netzwerks, Anbindung an das Internet, Schulseiten im WWW.
Schüler aus meinem Seminarkurs ‘Neue Technologien’ (Schuljahr 97/98, IKG Reutlingen)
OSR M. Schlipphak, Unterstützung beim Unterricht in Klasse 11, jetzt GK Mobiles Klassenzimmer
OSR M. Breddin, Projekt ‘Nathan’
OSR W. Jung, Klassenfahrt nach Kreisau
OSR F. Förstel, Musikzeitung Me-Me
Schul- Kultur- und Sportamt Stadt Reutlingen:
Herr Keppler, Reutlinger Schulen im Internet
Fachhochschule Reutlingen:
Prof. Dr. Obieglo, Rektor
Herr U. Poliak, Web-Administrator
Herr Nemeczek, Netzwerke
Fachhochschule Heibronn/Künzelsau:
Prof. Dr. W. Werner, Computeralgebra
Universität Tübingen:
Prof. Dr. W. Küchlin, Informatik, CAS, Dokumentenmanagement
Prof. Dr. W. Nakel, Didaktik
Universität Giessen:
Prof. Dr. U. Glowalla, kognitive und pädagogische Psychologie
Baden-Würtembergs Extended LAN (BelWue):
Herr Merdian und Frau Herrmann, Anbindung von lokalen Schulnetzwerken an das Internet
Landesinstitut für Erziehung und Unterricht (LEU):
Herr Meyer-Bothling, Herr Zaoral, Arbeitsgruppe Multimediales Lehren und Lernen
Deutsches Institut für Fernstudienforschung (DIFF):
Dr. U. Harms, vollständige Lernumgebungen (SLICE)
Frau H.Krahn Lernumgebung SLICE
Förderverein MNU:
OSD A. A Campo, SD. Dr. W. Riemer, SD J. Wulftange, Lehrplantagungen
Initiative Schulen ans Netz (SaN):
M. Drabe, Chefkoordinator
Wilfried Laurier University, Waterloo, Ontario, Kanada:
Prof. Dr. H. Schmidt, Webmaster des Internationalen Deutschlehrerverbands (IDV), Schüleraustausch
Fa. Nodus GmbH:
W. Ederer, Frau Rebmann, Programmierung des Domino-Servers
Fa. Waterloo Maple Software:
M. Monagan, T. Kahrmann, Software
Fa. Scientific Computers:
Dipl. Ing. D. Meerkamp (Geschäftsführer), Projektbegleitung, A. Himmeldorf , Software
International Thomson Publishing (ITP)
Freigabe der Materialien aus ‘Moderne Physik mit Maple’
Durch die starke Verflechtung von Pädagogik, Verwaltung und Technik wurden im Vorfeld und Verlauf des Projekts viele wertvolle Beziehungen aufgebaut. Ohne ein solches Beziehungsnetz wäre die Planung und Durchführung des Projekts niemals möglich gewesen. Mein besonderer Dank gilt Herrn Öttinger, dessen liberale Führung des CA-Projekts alle Beteiligten sehr zur Kreativität anregte, den oben genannten Schülern ‘der ersten Stunde’ und ihren Nachfolgern, Herrn Poliak für seine unermüdliche Bereitschaft, aus einem Lehrer einen Netzwerktechniker zu machen, Herrn Ederer für sein Know-How und seinen Idealismus, Prof. Küchlin für seinen Überblick und strategische Tips ‘just in time’, Ralph Jäger für sein ‘hohes Maß an Flexibilität’ und Herrn Merdian für seine schier unerschöpfliche Geduld.
Inhaltsverzeichnis
2.1 Computer-Algebra-Systeme in der Schule
2.2 Das Pilotprojekt am Isolde-Kurz-Gymnasium
2.3 Neue Technologien und Wissensbasis an der FH-Reutlingen
2.5 SaN-Infrastrukturprojekt ‘CAS-Server’
2.6 Anbindung des lokale Netzes an das Internet
3 Einbettung des Mathematikprojekts
3.2 Fächerverbindender Unterricht
4.1.1 Herkömmliche Materialien
4.1.2 Elektronisches Buch als neues Medium
4.1.2.1 CAS in Kombination mit einem elektronischen Buch (Worksheetkonzept)
5.1.2.4 Integralrechnung (in Klasse 11)
5.1.2.5 Folgen und Grenzwerte (Leistungskurs 12)
5.1.2.6 Gebrochen rationale Funktionen
5.1.2.7 Integralrechnung (Leistungskurs 12)
5.2 Unterrichtsformen und Methoden
7 Zusammenfassung und Ausblick
Liste der Anhänge (wird demnächst verlinkt):
1. Berichte über CAS-Einsatz am IKG vor dem Projekt (Auszüge)
Klasse 11, Physik- und Mathematikkurse, CAS-Kurse: Zwischenbericht und Abschlußbericht
2. Stoffverteilung und kurze Dokumentation des Unterrichts
Klasse 11:
Erste Phase (Technik) bis zu den Herbstferien 96 (doku1.mws)
Zur Organisation, Merkblätter für die Schüler (org1.mws)
Zweite Phase, mehr Mathematik, Herbst 96 bis Weihnachten (doku2.mws)
Halbjahres-Info für die Schüler (halbj.mws)
Halbjahres-Info für Eltern und Schüler (halbj.doc)
Januar bis Ostern 97 (doku3.mws)
Ostern bis Sommer 97 (doku4.mws)
Leistungskurs 12:
Erstes Halbjahr (tageb12.doc)
3. Klassenarbeiten, Referatthemen, Arbeitsblätter
Klasse 11:
Referate 1 (referate1.mws)
Klassenarbeit 6.12.96 (ka1l.mws)
Kommentare zur Klassenarbeit (ka1komm.doc)
Physikarbeit (phklal.mws)
Übungsblatt (uebung.mws)
Schriftliche Arbeit 21.3.97 (ka21.mws)
Referate 2 (Referate2.doc)
Zweiter Maple-Test (mtest2p.mws)
Leistungskurs 12:
Referate 1 (referate1.doc)
Übungsblatt zur KA 1,1 (handschriftlich)
KA 1,1 (ka11.mws)
Lösungen zur KA11 (ka11loes.mws)
KA 1,2 mit Lösungsskizze (ka12.mws)
Abitur 1999 siehe WWW
4. Didaktik
Mathematische Landschaft (mathcard.mws)
Computeralgebrasysteme im Unterricht (casu.mws)
Lernstufen (lernstufen.mws)
Aristoteles
5. Computer Algebra Systeme
Bericht für LEU (Ohne tabellarische Auswertung, siehe WWW)
6. Fortbildungen
Mössingen, Friedrichshafen, IKG, Physikfortbildungen, WWW-Fortbildungen, ...
| Denn es ist eines ausgezeichneten Mannes nicht würdig, wertvolle Stunden wie ein Sklave im Keller der einfachen Berechnungen zu verbringen. G.W.Leibniz, 1646-1716 |
In meiner eigenen Schulzeit (Abitur 1966) haben wir ein ganzes Schuljahr (nach heutiger Zählung Klasse 10) damit verbracht, Logarithmentafeln und den Rechenstab bedienen zu lernen. Wir mußten alle diese Techniken erlernen, egal ob aus uns später Kaufleute, Bürgermeister, Französichlehrerinnen, Ärzte oder Physiker wurden. Bei unserem 30-jährigen Abiturstreffen stellten wir dann fest, daß keiner von uns nach der Schule je wieder eine Logarithmentafel aufgeschlagen hat. Nur der Straßenbauingenieur hat ab und an noch den Rechenstab benutzt. Beim gleichen Abiturstreffen, bei dem auch unser Mathe-Lehrer - den wir alle hoch schätzen - anwesend war, konnte außer unserem Lehrer nur noch einer von uns etwas mit den Begriffen anfangen, die für die ‘Kurvendiskussion’ benötigt werden (er unterrichtet seit 20 Jahren Mathematik). Das Erlernen der Technik der Kurvendiskussion nahm zu unserer Schulzeit (wie heute auch) drei Jahre in Anspruch. Wir haben damals auch noch andere Techniken gelernt: Wie übersetzt man Cäsar, Vergil und Livius? Wir wissen nur noch, daß das einmal dran war - gebraucht hat es aber in ihrem 'Leben nach der Schule' nur die Lateinlehrerin. Aber wir sind alle davon überzeugt, daß wir in unserer Schulzeit das Denken gelernt haben. Ob das nun der ACI war oder die Logarithmentafel oder die Kurvendiskussion - spielt das eine Rolle? Wir haben aber in unserer Schulzeit noch mehr gelernt, nämlich uns zu verständigen und miteinander zu leben - ohne Lehrplan, ohne spezielle fachdidaktische Inhalte und Methoden: wir hatten einfach gute Pädagogen - Menschen - als Lehrer.
Der Rechenstab wurde bald vom Taschenrechner abgelöst. Wer von uns (Abi 66) den Taschenrechner wirklich benötigt, hat diese Technik auch ohne Lehrer und nach seiner Schulzeit beherrschen gelernt (interessant dabei ist vielleicht, daß ausgerechnet die Naturwissenschaftler und Mathematiker unter uns den Taschenrechner kaum verwenden, weil sie ebenso wie die Hausfrauen gelernt haben, im Kopf zu rechnen - nur nicht so schnell).
Der Taschenrechner wurde bald vom Computer überholt, und in den Computer pflanzte man Software ein, mit der man nicht nur Logarithmen berechnen konnte, sondern auch die Kurvendiskussion automatisieren kann: Computer-Algebra-Systeme (CAS). Auch die Übersetzung von Vergil per Knopfdruck kommt in Reichweite. Kommt es nur auf die Technik an? Auf die künstliche Intelligenz?
Ich wollte mit dieser etwas launigen Einleitung darauf hinweisen, daß ich nicht zu den Computerfreaks gehöre, die ein Millionenprojekt wie das ‘Mobile Klassenzimmer’ bedingungslos gut heißen und vorwärtstreiben. Auch oder gerade weil ich mich täglich mit den ‘Neuen Technologien’ herumschlage, frage ich täglich nach ihrem Wert. Nein, nicht nach dem materiellen, sondern nach dem wirklichen. Man könnte auch sagen, ich frage nach dem Sinn oder dem Ziel unseres Technologiefiebers - denn Fieber haben ja oft eine heilende Wirkung. Wie finden wir die Antwort auf diese Frage? Dazu gibt es naturgemäß eine sehr kontrovers geführte Diskussion (siehe cas.txt als Beispiel für die Modernisierung des MU). Das Spektrum der Meinungen reicht von einer völligen Blockade der neuen Technologien (sogar der Taschenrechner soll wieder abgeschafft werden) bis zu einer völligen Ablehnung des herkömmlichen Unterrichts (Computer als einziges Medium). Mit diesen Vorurteilen können wir uns nicht zufrieden geben, wenn wir einerseits mit der Entwicklung (Technisierung) Schritt halten wollen und andererseits Bewährtes bewahren wollen. Das Bewährte kennen wir, jedenfalls reicht hier unsere Kenntnis für einen Konsens aus. Das Neue kennen nur einige von uns und seine Folgen können nur wenige abschätzen. Hier müssen wir also die Antwort suchen: Die neuen Technologien sind kein von der Gesellschaft isoliertes Phänomen, das ‘über uns kam’. Wir haben es produziert, wir müssen damit fertig werden. Nur das ist der Ansatzpunkt (und die Rechtfertigung) eines Millionenprojekts - gerade in Zeiten leerer Kassen. Wir müssen voll ausloten, was auf uns zukommt. Angesichts der rasanten Entwicklung ist das äußerst schwierig und kann nur gelingen, wenn wir ein Pilotprojekt durchführen, das uns eine Extrapolation für die nächsten zehn Jahre erlaubt.
Aus diesen Gründen vertrete ich sozusagen zu Testzwecken hier das ‘progressive Lager’. Man wird nur dann beantworten können, was das Neue uns bringt, wenn man mit allen zur Verfügung stehenden Mitteln einen echten Härtetest wagt. Dies war und ist der Geist und die Zielsetzung des Pilotprojekts ‘Mobiles Klassenzimmer’.
Wir haben uns nicht blindlings in dieses Wagnis gestürzt, und angesichts der leeren Kassen muß man auch gute Gründe haben, wenn man ein Millionenprojekt beginnt. Die Durchführung muß wohl durchdacht sein und eine Auswertung muß entscheidend mehr bringen, als vorher bekannt war oder leicht durch kostenneutrales Nach- und Vorausdenken als bekannt eingestuft werden kann. Dabei lautet die zentralen Fragen (hier noch einmal konkret für das Projekt formuliert):
- Welche ‘Innovationen’ kommen auf uns zu (im MU und im Unterricht allgemein)?
- Was von diesen ‘Innovationen’ ist für die Didaktik (des MU) von Relevanz? (Was kann man nur mit dem Computer unterrichten, und was sollte man tunlichst ohne Computer unterrichten - gibt es ein experimentum crucis?)
- Wie setzen wir den positiven Teil der Innovationen flächendeckend in die Praxis um?
Ich werde in diesem Bericht versuchen, diese zentralen Fragen aufzuschlüsseln, wobei zunächst die auf den Vorarbeiten beruhende Planung und Realisierung der technischen Möglichkeiten im Vordergrund steht.
2.1 Computer-Algebra-Systeme in der Schule
Computer-Algebra-Systeme haben sich schon vor Jahren weltweit in der Forschung und Lehre etabliert und die Weiterentwicklung wird energisch von Weltfirmen und Akademikern vorangetrieben (siehe LEU-CAS). Dementsprechend gibt es inzwischen eine umfassende Literatur zu diesem Thema. (Hier seien stellvertretend genannt: GI, Prof. Küchlin, DIFF, Prof. Buchberger, CAS an Schulen: Heugl).
Man konnte also auf viele Erfahrungen und ein reichhaltiges Fachwissen aufbauen. Andererseits war es höchste Zeit, auch an den Schulen Anschluß an die Entwicklung zu bekommen. Deshalb wurde in Baden-Württemberg das zukunftsweisende CA-Projekt gestartet. Im Verlaufe dieses Projekts stellte sich heraus, daß das CAS Maple am besten für den Einsatz an Schulen geeignet war und immer noch ist (vgl. CAS-Berichte vom IKG).
Das CA-Projekt bestätigte aber auch die Vermutung, daß die Möglichkeiten der neuen Mathematiksoftware nur dann ausgeschöpft werden können, wenn dieses Werkzeug den Schülern ständig zur Verfügung steht (vgl. das österreichische DERIVE-Projekt). Also war es konsequent, einige Klassen mit Notebooks auszustatten, um die moderne Mathematik voll auszutesten. Dabei gab es zwei Aspekte:
- Der Test sollte Anhaltspunkte dafür liefern, inwiefern sich der MU für alle kurzfristig ändern würde, wenn man ein CAS einsetzt.
- Der Test sollte Auskunft darüber geben, was überhaupt mit einem CAS möglich ist, das in einer vernetzten Welt (Telelearning) eingesetzt wird.
2.2 Das Pilotprojekt am Isolde-Kurz-Gymnasium
Das Pilotprojekt sollte also sowohl in die Breite als auch in die Tiefe gehen. Am Isolde-Kurz-Gymnasium liegt der Schwerpunkt der Arbeit beim zweiten Punkt. Wie kamen wir zu diesem Auftrag der ‘Tiefenbohrung’? Durch meinen beruflichen Werdegang kann ich auf eine langjährige Erfahrung mit CAS zurückblicken: vor über 20 Jahren setzte ich im Rahmen meiner Promotion eines der ersten CASe (REDUCE) zu Berechnungen in der Teilchenphysik ein. Es folgten Fortbildungen zur Quantenphysik, die ich mit dem CAS Mathematica durchführte. Und schließlich die Teilnahme am CA-Projekt Baden-Württembergs (siehe Bericht...). Dabei war es mir wichtig, CA nicht nur in den speziell dafür eingerichteten Kursen einzusetzen, sondern auch im laufenden Unterricht (Mathematik und Physik), um Erfahrungen über die Verwendungsmöglichkeiten von CAS im Schulalltag von morgen zu sammeln. So entstand mein Buch ‘Moderne Physik mit Maple - von Newton zu Feynman’. Auf den ersten Blick mag dieses Buch nicht viel mit der Verwendung von CAS in der Schulmathematik zu tun haben, aber der Schein trügt: Newton hat für seine Physik die Infinitesimalrechnung entwickelt, die wir heute von Klasse 11 bis 13 unterrichten (am besten fächerverbindend mit Physik). Feynman hat die Methode der linearen Approximation so genial eingesetzt, daß er mit seinen Pfadintegralen einen neuen und leicht nachvollziehbaren Weg in die Quantenphysik aufzeigte. Alles Themen, die für den Unterricht in den Klassen 12 und 13 (Mathematik und Physik) nicht nur von elementarer Bedeutung sind, sondern auch hochinteressant. Werden diese Themen mit einem CAS behandelt, so lernt der Schüler, das Forschen und der Lehrer die bewährte Struktur der Didaktik mit CAS: Der Einsatz eines CAS in einem Unterricht, in dem die Lösung von Problemen im Vordergrund steht, setzt beim Schüler und Lehrer solide Grundkenntnisse im Umgang mit dem CAS voraus.
2.3 Neue Technologien und Wissensbasis an der FH-Reutlingen
Parallel zur Entwicklung der CASe lief in den letzten Jahren eine ‘zweite’ Entwicklung: Die neuen Technologien - von der Vernetzung bis zu Multimedia. Natürlich ist das die Entwicklung, in die der Fortschritt der CASe eingebettet ist. Über die Fachdidaktik der Mathematik hinaus, war es also von entscheidender Bedeutung, diese Entwicklung in das Projekt mit einzubeziehen, denn schließlich kann ein Notebook ja nicht nur in Mathematik eingesetzt werden. Will man aber die Möglichkeiten der neuen Technologien voll nutzen, so geht das nur mit einer konsequenten Planung (Siehe Erfurt und Schwellen).
Die zusätzliche Aufgabe bestand am IKG also darin, eine Wissensbasis und Kommunikationsplattform aufzubauen, die von den vier Projektschulen zum Austausch von Materialien (Maple-Arbeitsblättern), Meinungen und Berichten genutzt werden konnte. Schon ein Jahr vor Beginn des Projekts hatte ich an der FH-Reutlingen Internet-Seiten für unser Gymnasium eingerichtet. Deshalb lag es nahe, diese Aufgabe auf einem Rechner der FH in Angriff zu nehmen und es entstand in den Sommerferien 96 eine Verzeichnisstruktur, die paßwortgeschützt nur den Teilnehmern des Projekts zugänglich war und über die notwendige Funktionalität verfügte. Außerdem wurde eine Datenbanklösung projektiert, die ein Dokumentenmanagement ‘state of the art’ ermöglichen sollte. Ich möchte mich an dieser Stelle beim Rektor der FH-Reutlingen, Prof. Obieglo, für die Gastfreundschaft bedanken. Herr U. Poliak stand (und steht) uns mit seinem Know-how als Administrator stets zur Verfügung - er hat den größten Anteil am Gelingen der anspruchsvollen Aufgabenstellung. Herr Prof. Küchlin (Universität Tübingen) gab uns nicht nur richtungsweisende Tips zur Entwicklung auf dem Sektor des Dokumentenmanagements, sondern auch viel Motivation.
2.4 Fortbildungen
Ebenfalls in der Vorbereitungsphase des Projekts konnte ich CAS-Fortbildungen (Mathematik und Physik) und Internet-Fortbildungen halten (zum größten Teil an unserer eigenen Schule) und dabei wertvolle Erfahrungen über die Meinungen und Wünsche der zukünftigen Adressaten (Lehrer) sammeln. Die Quintessenz dieser Erfahrungen lautet: Wir müssen es vermeiden, einen technikzentrierten Unterricht anzustreben, in dem das Handling und der Knopfdruck im Vordergrund steht. So paradox diese Feststellung in einem Bericht klingen mag, der den konsequenten Einsatz der neuen Technologien im wesentlichen befürwortet: Die allgemeinen Befürchtungen und die Skepsis den Innovationen gegenüber sind durchaus gerechtfertigt. Wir betreten Neuland, absolutes Neuland für viele. In einer solchen Situation neigen die Pioniere dazu, alles ‘was machbar ist’ unkritisch auch zu machen und weiter zu empfehlen, denn es funktioniert ja so schön. Oft geht dabei das Augenmaß für den sinnvollen Einsatz der Technik verloren. Das bekannteste (und banale) Beispiel ist wohl der Mißbrauch der Textverarbeitung: In stundenlanger Arbeit wird an dem Layout eines Arbeitsblattes gefeilt. In der gleichen Zeit hätte man eine Menge Skizzen von Hand in viele verschiedene Arbeitsblätter eingefügt und dabei noch viel Zeit gehabt, über den didaktischen Wert der Aufgabenstellung nachzudenken. Dazu kommt, daß die neuen Technologien erst in den Kinderschuhen stecken. Sie sind bei weitem noch nicht so benutzerfreundlich, wie es für einen verstärkten und flächendeckenden Einsatz erforderlich wäre, seien es nun CASe, Lernsoftware oder die Software für die Verwaltung von Schulnetzen. Überall ist mehr oder weniger Spezialwissen verlangt, das schon morgen wieder überholt ist. Die jungen Schüler eignen sich das fast mühelos an (und vergessen es fast ebenso schnell wieder wie das, was sie kurz vor einer Klassenarbeit lernen). Niemand kann es aber einem 60-jährigen Kollegen, der zum erstenmal in seinem Leben versucht, sich mit der Maus durch einen Verzeichnisbaum zu klicken, verdenken, wenn er sich von dieser Art des Arbeitens nicht angezogen fühlt. Dennoch können wir es uns nicht leisten, den Kopf in den Sand zu stecken, vielmehr müssen wir lernen, kompetent mit den Innovationen umzugehen, ja es ist unsere Aufgabe, die Technik so zu gestalten, daß sie sich nicht verselbständigt, sondern menschenfreundlich bleibt.
Vielleicht zeigt eine E-Mail von Herrn Meyer-Bothling (Mitglied der AG ‘Multimediales Lehren und Lernen’ am LEU) besser die Fortbildungsproblematik auf, als ich das mit eigenen Worten kann:
Lieber Herr Komma,
das blaue Heft könnte - auf den ersten Blick - etwa diesen Inhalt haben:
Einführung wie der Leumedi@-Artikel, Bewertender
Vergleich der CAS, ausführlich und als Tabelle,
Bildschirmausdrucke,
möglicher Unterrichtsverlauf mit pädagogischer Bewertung,
Beispiele von Schülerarbeiten,
Neuentwurf des Oberstufen-Lehrplanes,
Angemessene Prüfungen - schriftlich und mündlich.
Das wäre natürlich ein anspruchsvolles Paket, aber es
wäre auch
eminent lesenswert für alle, die sich ernsthaft mit dieser Art von
Unterricht auseinandersetzen wollen.
Auf den zweiten Blick kommen mir noch einige Fragen:
Wie gestalten Sie den Übergang? Wie lernen die Schüler
den Umgang mit
dem neuen Werkzeug? Wie werden sie motiviert und welche Schritte
folgen? Welche Klippen gilt es nach Ihrer Erfahrung zu umschiffen?
Was empfehlen Sie all denen, die nicht den Sprung ins Tiefe wollen?
Läßt sich ein CAS sporadisch einsetzen? Ich meine ein
CAS mit seinen
vielfältigen Möglichkeiten und nicht einen Funktionsplotter. Die
Frage ist dann ja: Wieviel Unterricht braucht man, damit sich der
Aufwand lohnt, den Umgang mit dem Programm und die eigene Sprache
erstmal zu lernen?
In welchen Gebieten des Mathe-Lehrgangs ist ein solcher sporadischer
Einsatz denkbar? Gibt es vielleicht sogar Berichte über
sporadischen
Einsatz, auf die Sie verweisen könnten?
Was soll man nach sporadischem Einsatz mit der
herkömmlichen
Abi-Prüfung anfangen?
Vielleicht müssen wir uns überhaupt zwischen zwei
Möglichkeiten
entscheiden:
(1) Bericht für Entschlossene - Ihr Unterrichtsgang mit
Folgen
für Prüfung und Lehrplan.
(2) Empfehlungen für Interessierte - wie kann man
sich dieser Art von Unterricht nähern, ohne sich gleich auf mehrere
Jahre festzulegen.
Ich halte beide Zugänge für Interessant. Was meinen Sie?
Machen Sie's gut
Claus Meyer-Bothling
Es würde den Rahmen dieser vorläufugen Dokumentation sprengen, wenn ich auf alle diese wichtigen Fragen eingehen wollte. Sie stehen aber ständig im Hintergrund des ‘Mobilen Klassenzimmers’ und ihre Beantwortung wird früher oder später kommen müssen. Vielleicht wird sie auch hier zum Teil gegeben.
2.5 SaN-Infrastrukturprojekt ‘CAS-Server’
In der weiteren Entwicklung konnten diese Erfahrungen (Wissensbasis an der FH-Reutlingen und Fortbildungen) gewinnbringend im SaN-Infrastrukturprojekt ‘CAS-Server’ (siehe ...), das ich seit Juni 97 an unserer Schule durchführe verwendet werden. Bei diesem Infrastrukturprojekt handelt es sich um eine Wissensbasis und Kommunikationsplattform, die mit einem Lotus Notes Datenbank-Server realisiert wird. Er dient dazu, die vier Pilotschulen (Mobiles Klassenzimmer) und die zur Zeit etwa 40 CAS-Schulen Baden-Württembergs zeitgemäß zu vernetzen. Im Vordergrund stand bei den Entwicklungsarbeiten die Bemühung um eine nicht technikzentrierte Lösung. Dazu muß die Technik so gut sein, daß man sie nicht mehr bemerkt, nur so kann Akzeptanz bei einem breiten Publikum erreicht werden. Dies erfordert aber ein hohes Maß an Funktionalität. (Vergleich: Wer heute einen Mercedes fährt, weiß in der Regel nicht, was alles ‘unter der Haube steckt’ und weshalb es so leicht und komfortabel ist, Auto zu fahren. Weil so viel Technik unter der Haube steckt, bemerkt man sie nicht mehr und jeder kann sie nutzen. Hohe Funktionalität erreicht man aber nur mit dem Wissen von Spezialisten. Glücklicherweise konnte ich in Reutlingen eine Firma für Netztechnik ausfindig machen, in der nicht nur Spezialisten sondern Idealisten arbeiten: Herr Ederer und Frau Rebmann von der Fa. Nodus GmbH haben uns einen Datenbank-Server ‘state of the art’ programmiert und darüber hinaus viele Anregungen dazu gegeben, wie man das gesamte Unterrichtsgeschehen auf das Medium Computer und Internet abbildet. Das ist nicht technikzentriert - nur die Entwickler arbeiten so technikzentiert, daß die Technik in den Hintergrund tritt. Nun können unter der Internet-Adresse https://cas.mikomma.de Materialien weltweit ausgetauscht werden, Diskussionen geführt werden und der Arbeitsfluß kann gesteuert werden.
2.6 Anbindung des lokale Netzes an das Internet
Bevor man ein lokales Netz an das Internet anbindet, muß es vorhanden sein und lokal funktionieren. Durch großzügige Elternspenden konnten wir lange vor Projektbeginn in unserem Computerraum ein Netz mit 10 Arbeitsstationen und einem Server finanzieren. In einem Betrieb kalkuliert man bei der Einrichtung von Netzen etwa 30% für die Anschaffungskosten und 70% (jährlich) für die Wartung. Man kann sich leicht ausrechnen, daß die 70% bei einem ‘Betrieb’ unserer Größenordnung (80 Kollegen und mehr als 1000 Schüler) einer vollen Stelle entsprechen. Wir hatten (und haben) aber weder eine volle Stelle, noch einen Sponsor für die fehlenden 70%. Da helfen nur Idealisten (‘Computerfreaks’). Ohne meinen Kollegen Schlipphak und ‘unseren’ Computerhändler Wienold hätte ich es nie geschafft, von ‘heute auf morgen’ (in den Weihnachtsferien ...) ein Novell-Netz zum Laufen zu bringen. Aber da war nicht nur der Kollege Schlipphak - wir haben auch Schüler! Zuerst kam Ralph Jäger, dann Thomas Altmann, Armin Scheurer, Julian Gonska und Holger Braun (alle Abitur 97). Sie waren nicht nur in den Gründerjahren der ‘Technologie am IKG’ die treibenden Kräfte, sie haben auch die entscheidenden Entwicklungen durch ihren Arbeitseinsatz und ihr Know-how mitgetragen: Laufende Updates haben eben ihren Preis - vor allem personell. Im Zuge des Infrastrukturprojekts ‘CAS-Server’ bekam unsere Schule zwei weitere Windows NT - Server und wir stellten sukzessive das ganze Netz auf Windows NT und Windows 95 um. Schließlich kam die Standleitung zum BelWue und ein Router, der konfiguriert sein wollte. Ralph Jäger hat auch davor nicht zurückgeschreckt, und wir haben einiges dabei gelernt. Aber ohne die Unterstützung unseres neuen (zweiten) Providers BelWue wären wir wohl nicht so schnell mit der Technik ‘fertig geworden’. Dank sei Herrn Merdian und Frau Herrmann, die uns aus bei den ersten Schritten kräftig unterstützten und uns auch weiterhin gut betreuen und versorgen: das sind echte Provider! Nun sind wir Partner- und Referenzschule von Microsoft und bekommen kostenlose Updates, die wir kostenneutral installieren...
In der Planungsphase des Pilotprojekts wurde ich vom MKS u.a. damit beauftragt, Notebooks zu testen. Zusammen mit einem Team aus Computerhändlern, Netzwerkspezialisten, Kollegen und Schülern machte ich mich an die Arbeit und prüfte die zur Verfügung stehenden Modelle auf ‘Herz und Nieren’ (RAM&ROM). Neben der Robustheit (für den täglichen Einsatz und Transport), der leichten Bedienbarkeit, der Rechengeschwindigkeit und der Kapazität der Akkus hoben wir in unserem Bericht (siehe...) zwei wichtige Auswahlkriterien hervor:
- Die Geräte müssen ein aktives (selbstleuchtendes) Display besitzen.
- Das Diskettenlaufwerk sollte integriert sein, ein CD-ROM-Laufwerk ist sekundär und kann extern angeschlossen werden.
- Integriertes Netzteil.
Wir bekamen IBM-Tinkpads 365 mit passivem Display, externem Diskettenlaufwerk (und einem integrierten CD-ROM-Laufwerk) und externem Netzteil.
Das passive Display kann nur gut gelesen werden, wenn man direkt davor sitzt. Das erschwert die gemeinsame Arbeit an einem Notebook (z.B. Erklärung durch den Lehrer oder Mitschüler) außerordentlich.
Das externe Diskettenlaufwerk mußte inzwischen (halbe Laufzeit des Projekts) mehrfach ausgetauscht werden und das interne CD-ROM-Laufwerk ist störanfällig. Aber das Schlimmste ist, daß bis heute über die Hälfte der Notebooks (auch an den anderen Projektschulen) zur Reparatur eingeschickt werden mußten, weil sie beim Startvorgang bei der Abfrage des externen Diskettenlaufwerks stehen bleiben. Die Reparatur besteht im Austausch des Motherboards (nach Auskunft der Fa. Taylorix), ist aber nicht endgültig wirkungsvoll, weil schon mehrere Thinkpads zweimal repariert werden mußten. Die Reparaturzeiten liegen z.T. über vier Wochen. Angesichts dieser starken Beeinträchtigung ist es fast überflüssig zu erwähnen, daß die externen Netzteile nun auch allmählich ‘ihren Geist aufgeben’ (Kabel und Stecker sind der Belastung nicht gewachsen).
Allerdings: In Kanada läuft ein Projekt, in dem eine Universität (Acadia) mit tausend Thinkpads 365 ausgestattet wurde. Man sollte sich mit der dortigen Projektleitung in Verbindung setzen!
Trotz der massiven Schwierigkeiten mit dem Modell haben wir an unserer Schule die Vernetzung konsequent weitergeführt und erhielten dazu Netzwerkkarten, mit denen die Notebooks an das LAN angeschlossen werden können (vorläufig 10). Somit können die Schüler des Projekts ihre Arbeiten direkt auf einem der Server abgeben, neue Aufgaben direkt auf ihr Notebook kopieren und mit ihrem Notebook alle Dienste des Internets nutzen.
3 Einbettung des Mathematikprojekts
In dem Projekt sollten keine ‘geistigen Überflieger’ teilnehmen (weder Schüler noch Lehrer), sondern man suchte ‘Normalschüler’ und ‘Normallehrer’, damit abgeschätzt werde konnte, inwieweit sich die im Projekt gemachten Erfahrungen flächendeckend übertragen lassen. Dieser Ansatz ist zwar berechtigt aber auch nicht unproblematisch, denn zumindest was die Ausstattung angeht (Laptops), wird sich in naher Zukunft keine flächendeckende Versorgung erreichen lassen. Dagegen ist eher zu erwarten, daß die rasch zunehmende Vernetzung (auch mit privaten PCs) eine Art virtuelle Schule entstehen wird. Man wird also die Daten nicht im Computer oder auf Diskette transportieren, sondern auf Leitungen und an stationären Computern arbeiten. Aus diesem Grund liegt ein Schwerpunkt des Projekts am IKG auch beim Einsatz der Netzwerke. Abgesehen von dieser technischen Argumentation sollte ein Pilotprojekt auch weitreichende Extrapolationen erlauben, die sich gerade nicht am heutigen ‘Normalzustand’ orientieren, sondern an dem, was morgen möglich sein wird.
Dennoch haben wir am IKG dafür gesorgt, daß eine ‘normale Klasse’ ausgewählt wurde und nicht eine Eliteklasse. Dies geschah durch Auslosung unter den beiden zehnten Klassen, die sich komplett gemeldet hatten, und es hat sich auch bewährt.
In sozialer Hinsicht handelte es sich um eine gewachsene Klasse mit intaktem Gefüge. Die ausgeprägte Hilfsbereitschaft und die im Laufe des Projekts deutlich zunehmende Selbstorganisation bilden eine tragfähige Grundlage für die erhöhten Anforderungen in diesem Projekt.
Auch fachlich war (und ist) der Leistungsstand der Klasse ‘normal’, d.h. Rechenschwächen auch ohne CAS (wie ein Vortest zeigte), und die üblichen Probleme bei Transferaufgaben.
Hier kann man aber schon jetzt vorwegnehmend sagen, daß eine Besserung durch Trainingsprogramme und das Projekt an sich eingetreten ist. Man kann es sich als Teilnehmer eines solchen Projekts nicht leisten, nicht rechnen zu können - das Projekt wirkt selbstregulierend. Aber auch die in jeder normalen Klasse zu findende ‘Schere’ ist zu beobachten und wird durch den Unterricht mit CAS u.U. weiter geöffnet. Das schadet aber nichts, denn ein Projekt kann in die Breite, es kann aber auch in die Tiefe gehen - und insbesondere ein Pilotprojekt sollte in die Tiefe gehen (vgl. Halbjahresinfo).
Nicht nur die Schülerbefragung zeigt, daß sich die Schüler außerordentlich stark engagieren und aus eigenem Antrieb Aufgaben übernehmen, die weit über den Mathematikunterricht hinausgehen. Stellvertretend für die recht breite Spitze der Klasse sei hier Fabian Hust erwähnt, der im Schnitt etwa 10 Stunden pro Woche investiert, um die Seiten des ‘Virtuellen Klassenzimmers’ beim BelWue auf dem Laufenden zu halten.
3.2 Fächerverbindender Unterricht
Damit sich die Investition auch lohnt, sollten die Notebooks nicht nur in Mathematik eingesetzt werden. Sie sind deshalb voll multimediafähig (CD, Soundkarte, Lautsprecher, Mikrophon) und wurden am IKG auch (zur Hälfte) mit Netzwerkkarten bestückt. Nach einer Eingewöhnungsphase, in der sie ausschließlich in Mathematik eingesetzt wurden, war es den Schülern freigestellt, sie auch in anderen Fächern zu verwenden. Dadurch hat sich ‘fast von selbst’ ein fächerverbindender Unterricht ergeben - einfach durch das (Multi-)Medium. Zunächst haben wir das Notebook auch in Physik eingesetzt, weil ich in diesem Fach eine längere Vertretung übernahm und aus den vorangehenden Jahren schon einige Worksheets und auch Unterrichtserfahrung beisteuern konnte.
In Deutsch ergab sich dann das ‘Nathan-Projekt’, das von Hern Breddin durchgeführt wurde, und nun in Klassenstufe 12 Goethes Faust (Frau Bonnet).
In Geschichte wurde die Klassenfahrt nach Kreisau dokumentiert (Herr Jung).
Nun sind einige der ‘Laptop-Schüler’ auch in meinem vorgezogenen Seminarkurs und so kann hier der fächerverbindende Unterricht fortgesetzt werden:
In Musik wird die Zeitschrift Me-Me herausgegeben (Herr Förstel) und inzwischen ist jeder Schüler dabei, seine eigenen Internetseiten auf dem Notebook zu erstellen. Hier seien besonders hervorgehoben:
Science - World Launcher (Mathematik, Astronomie, Chemie, Physik, Stephan Simon) und
The House of Blues (Armando Häring). Es entstehen aber laufend weitere Seiten, die auch durchaus fachliche Qualität aufweisen.
Darüber hinaus hat nun jeder Schüler seine eigene E-Mail-Adresse und kann seine Post wahlweise im LAN, auf dem Notebook oder zu Hause abholen. Durch diese außermathematische Nutzung der Geräte haben die Schüler sicher sehr viel gelernt: Die Bedienung der Programme (vom System und Netzwerk über E-Mail und Hypertext bis zum Filetransfer und der Organisation und Pflege von Webseiten) steht dabei auf den ersten Blick im Vordergrund, aber wichtiger sind die ‘nebenbei’ erworbenen Qualifikationen der Kooperation und Bereitschaft zur Verantwortung, die auch von allen anderen Kollegen, die in der Klasse unterrichteten immer wieder lobend erwähnt wurden.
Durch diese Aktivitäten und unsere Präsenz im Internet kam es schließlich zu einer Einladung nach Kanada, die wir nun an Pfingsten wahrnehmen können. Und wieder ‘wie von selbst’: Die neuen Technologien (und ihr konsequenter Einsatz) haben Kontakte ermöglicht, die nun zum bilingualen Unterricht und interkulturellen Austausch führen.
3.3 Schülerbefragung
Am IKG wurde die erste Schülerbefragung kurz nach Beginn des zweiten Halbjahres durchgeführt. Man hätte den Zeitpunkt vielleicht früher wählen sollen, um die Entwicklung möglichst vollständig zu dokumentieren, aber andererseits hatten so die Schüler genügend Zeit, sich eine Meinung zu bilden:
1. Umfrage IKG, 11d, März 1997, 25 von 27 Schülern anwesend
Vorkenntnisse:
| Computer | Windows 3.x | Windows 95 | Textverarbeitung | Programmieren | Internet | Mathe-Prgre. |
24 |
19 |
10 |
20 |
4 |
5 |
3 |
Weitere Vorkenntnisse (Computer / Informatik):
Pascal 4, Mathplus 1, Scientific Workplace 1, Multimedia 1, Visual Basic 1, DOS 1.
Arbeitszeit im Projekt in Stunden pro Woche außerhalb des Unterrichts (auch ‘freiwillige Arbeit = Hobby’ und Wochenende):
1 |
2 |
3 |
4 |
5 oder mehr |
|
insgesamt |
0 |
1 |
10 |
6 |
8 |
am Notebook |
1 |
4 |
10 |
3 |
4 |
im Computerr. |
5 |
3 |
0 |
1 |
0 |
Ohne Computer |
11 |
1 |
2 |
||
Mit Maple |
1 |
14 |
6 |
1 |
3 |
Wo treten Probleme auf?
| Notebook | Windows | Maple | selbst. Arbeiten | U-Tempo | Mathematik |
0 |
1 |
13 |
6 |
1 |
3 |
Ich denke, daß Mathematik mit dem Computer
| leichter ist | schwieriger ist | Spaß macht | anspruchsvoller | überfordert | |
10 |
7 |
23 |
1 |
0 |
Für meine Hobbies (Vereine, Sport, Musikunterricht, Computer,...) nehme ich mir so viele Stunden pro Woche Zeit:
1 |
2 |
3 |
4 |
5 |
6 oder mehr |
5 |
20 |
Für meine Hausaufgaben (alle Fächer) benötige ich (Stunden pro Woche):
5 oder weniger |
6 |
7 |
8 |
9 |
10 oder mehr |
5 |
7 |
10 |
2 |
1 |
0 |
Man entnimmt der Befragung, daß wir mit einer ‘normalen Klasse’ in das Projekt gingen, was die Vorkenntnisse angeht (insbesondere Mathematik-Programme und - zum damaligen Zeitpunkt - Windows 95).
Die in das Projekt investierte Arbeitszeit ist verglichen mit den Hausaufgaben in allen Fächern außerordentlich hoch, wobei der Arbeitsanteil für Maple niedrig ist, obwohl Maple bei den ‘Problemen’ an erster Stelle steht.
Als zweites Problem wird das selbständige Arbeiten genannt, was aber sicher dadurch relativiert wird, daß ‘Mathematik mit dem Computer praktisch allen Spaß macht’.
Die Frage nach den Hobbys dient nur als Vergleichsmarke. Ebenso die Frage nach den Hausaufgaben.
Zum Schuljahreswechsel erschien keine Umfrage erforderlich, denn die Schüler hatten mit den Füßen abgestimmt: Von 27 Teilnehmern entschieden sich 21 für den Leistungskurs und 6 für den Grundkurs.
Die nächste Befragung wird im März 98 durchgeführt (Fragestellung mit feinerem Raster und unter Beteiligung der Schüler).
4 Technik
Im Verlauf des Projekts stand zur Verfügung bzw. wurde nachgerüstet...
4.1.1 Herkömmliche Materialien
Das herkömmliche Buch wurde nur als Aufgabensammlung und für Zusammenfassungen verwendet. Alle anderen herkömmlichen Materialien (Tafel, Kreide, Kopien, Projektor...) wurden situationsbedingt eingesetzt, also keine Fixierung auf den Computer.
4.1.2 Elektronisches Buch als neues Medium
Da die Unterrichtsinhalte (siehe...) weitgehend feststanden (auch was die zeitliche Planung betrifft - Stoffverteilung), konnte zur Einführung der Infinitesimalrechnung in Klasse 11 auf das ‘Buch Moderne Physik mit Maple’ zurückgegriffen werden. Die entsprechenden Worksheets wurden dem MU in Klasse 11 angepaßt, in Release 4 umgeschrieben, durch neue ergänzt und mit Hyperlinks versehen, so daß ein ‘Elektronisches Mathematikbuch’ entstand. Für die Klassenstufen 12 und 13 wird das Elektronische Buch laufend erweitert. Dieses Buch, das allen Teilnehmern des Projekts im Internet zur Verfügung steht, und sich laut Statistik auch außerhalb des Projekts einer regen Nachfrage erfreut (siehe MMM@WWW), übernimmt im Unterricht weitaus mehr Funktionen als ein herkömmliches Buch. Ich möchte sogar behaupten, daß ein Elektronisches Buch das Paradebeispiel für die Änderungen des Unterrichts durch die neuen Medien ist, wie man an folgender Gegenüberstellung sieht:
Gedrucktes Buch: Hinführende Texte (Begriffsbildung), Aufgaben, Erläuterungen, Orientierung (Inhalt und Index), manchmal auch Lösungen und Kontrollfragen.
Elektronisches Buch: Alle Merkmale eines herkömmlichen Buchs, dazu kommt:
Keine Alterung, ständig aktualisierbar, frei kopierbar (das freut den Schulträger)
Wesentlich neu ist aber die interaktive Arbeit mit einem Elektronischem Buch und die Möglichkeit, zur Kapselung der Inhalte und Methoden in verschiedenen Tiefen (siehe...).
Das Worksheet-Konzept: Lösungen können im Buch erarbeitet und kontrolliert werden.
Buch und Heft in einem, Ergebnissicherung an Ort und Stelle (individuell oder für die Klasse verbindlich).
Aufgaben können leicht variiert werden.
Anmerkungen und Ergänzungen können in das persönliche Buch eingetragen werden (als Text und als Befehlszeilen).
Eigene Hyperlinks ermöglichen das Auffinden von Information und fördern Assoziationen.
Das Inhaltsverzeichnis bietet nicht nur eine lineare Struktur, sondern über Hyperlinks eine Verflechtung der Inhalte (z.B. verschiedene ‘Touren’).
Ein vorgegebener Index ermöglicht interaktives Suchen und kann vom Anwender selbst ergänzt werden.
Das Buch steht bei der Klassenarbeit zur Verfügung (und wird zum Teil auch durch ausdrückliche Bezugnahme in der Fragestellung benutzt).
In einem Apparat können Hilfestellungen gegeben werden (Glossar, allgemeine Kommentare zur Didaktik, spezielle Tips und Lösungen, multimedial...).
Dazu kommen bei einem elektronischen Buch noch die bekannten Möglichkeiten multimedialer Anwendungen, die - konsequent eingesetzt - eine vollständige Lernumgebung schaffen. Wir sind im Projekt noch ein gutes Stück von der Perfektion entfernt, aber es ist schon jetzt sichtbar, daß diese Techniken ungeahnte Möglichkeiten mit sich bringen, die den Unterricht (allgemein) nicht effizienter sondern auch reicher machen.
4.1.2.1 CAS in Kombination mit einem elektronischen Buch (Worksheetkonzept)
Die wichrigsten Aspekte
Kapselung: Der Lehrer (Autor) hat die Möglichkeit, das CAS in verschiedenen Tiefen zugänglich zu machen und die Aktionen des Schülers zu steuern (Heugl: Black-Box / White-Box). Das Buch ist so geschrieben (und wird so weiter geschrieben), daß damit einerseits Schüler, die ein weniger ausgeprägtes mathematisches Talent haben, zurecht kommen, und andererseits Gipfelstürmer noch genügend Aufstiegschancen haben (vgl. Didaktik...).
Elektronische Bibliothek: Ergänzung des Elektronischen Buchs durch eigene Worksheets und Worksheets aus der Wissensbasis der Schule und aus dem Internet.
Projektarbeit: Hier nehmen die Referate, die in Gruppen erstellt und von Schüler zu Schüler beliebig ausgetauscht werden können eine wichtige Funktion ein (s.u.)!
Bei der Durchsicht des Buches in gedruckter Form sollte beachtet werden, daß es einiger Maple-Kenntnisse bedarf, sich allein durch die ‘Lektüre’ der Befehle einen Eindruck davon zu verschaffen, was dieses Buch bei interaktivem Gebrauch leistet. Außerdem ist zu beachten:
Die Schüler sind es inzwischen gewohnt, längere Befehlspassagen, die nur dazu dienen, eine bestimmte Art der Darstellung zu erreichen, aber für das Verständnis der Mathematik nicht wesentlich sind, zu überlesen (‘sichtbare Black-Box’).
Es werden grundsätzlich alle Worksheets zunächst von den Schülern erarbeitet und dann die sich ergebenden Fragen gemeinsam besprochen.
Die Worksheets werden mit unterschiedlichem Gewicht und mit unterschiedlichem Grad an allgemeiner Verbindlichkeit behandelt. ‘Pflichtstoff’ wird rechtzeitig vor Klausuren bekannt gegeben.
Die Schüler können sich individuelle Notizen in die Worksheets schreiben und Verknüpfungen anlegen.
Die Schüler können sich Worksheet-Teile kopieren und daraus eigene Worksheets erstellen, die ihren Neigungen und Fähigkeiten entsprechen. So können z.B. Befehlspassagen für die Profis in Sections gekapselt werden (unsichtbar gemacht werden, ohne daß das Worksheet seine Funktionalität verliert), oder ganz gelöscht werden.
Das Buch dient somit als ‘Rückgrat’ für den Verlauf des Unterrichts (nicht linear sondern verlinkt!) und als Ausgangspunkt für eigene Produkte der Schüler.
Kritiker, denen offensichtlich der oben genannte Hintergrund nicht bekannt war, kamen schon zu erheblichen Fehlinterpretationen unseres CAS-Unterrichts.
Das eigene Notebook des Schülers und die darauf installierte Software sollten für die Mobilität und ständige Verfügbarkeit des Mediums sorgen. Das ist eine technische Zielsetzung des Projekts. Das zweite und gleichrangige Ziel ist es, auch für eine Vernetzung zu sorgen. Aus einem einfachen Grund: Es wird in absehbarer Zeit nicht möglich sein, alle Gymnasiasten mit einem Notebook zu versorgen, aber es war schon zu Beginn des Projekts absehbar, daß sich die Vernetzung bald realisieren läßt. Der Schüler muß also nicht seine Arbeitsblätter in der Schule in sein eigenes Notebook eintippen, das Notebook nach Hause tragen und dort mit diesem Gerät weiterarbeiten. Er arbeitet in der Schule mit einem (stationären) Computer des Schulnetzes, geht nach Hause und arbeitet dort mit dem eigenem PC (der schon bald in jedem Haushalt stehen wird) weiter. Der Lehrer macht das gleiche. In einer vernetzten Welt wird die Mobilität überflüssig. Man transportiert weder Disketten noch ganze Rechner (Notebooks), man transportiert nur noch Daten - über Leitungen. Dazu muß man nicht einmal selbst in die Schule oder nach Hause gehen: Telelearning.
Der mobile Computer war aber eine notwendige Übergangslösung, denn die Entwicklung der neuen Technologien beschleunigt sich ständig und wir stehen vor der Aufgabe, mit den heute zur Verfügung stehenden und finanzierbaren Mitteln zu erkunden, wie wir uns in der technologisierten Welt von morgen zurechtfinden können.
Das Medium dominiert zur Zeit die Aktion. Damit müssen wir uns abfinden. Aber das Medium eröffnet auch viele neue Aktionen. Am Isolde-Kurz-Gymnasium haben wir versucht, der rasanten technischen Entwicklung in folgenden Schritten gerecht zu werden:
Die Maple-Worksheets müssen in geordneter und übersichtlicher Form auf den Notebooks der Schüler vorliegen und mit geeigneten Konventionen weitergegeben (‘hochgeladen’) werden. Fabian Hust hat dafür zwei Programme geschrieben. Der ‘MWS-Explorer’ ist eine für diesen Zweck spezialisierte Datenbank, in der die Schüler ihre Beiträge auf ihren Notebooks archivieren. Das ‘MWS-Uploadtool’ standardisiert die Abgabe der Beiträge im lokalen Netz (LAN).
Das LAN wurde so eingerichtet, daß jeder Benutzer sein eigenes Verzeichnis hat und somit der gesamte Kurs Materialien lokal zur Verfügung stellen kann (innerhalb der üblichen Verzeichnisstruktur). Von hier kann sich auch der Lehrer Beiträge auf den Home-PC holen und die Interna regeln (ebenso Schüler mit DFÜ-Anschluß).
Jeder Schüler verfügt über eine eigene E-Mail-Adresse und ist somit für alle Beteiligten zum Zweck der internen Kommunikation über das Netz zu erreichen.
An der Fachhochschule Reutlingen und am Belwue wurden WWW-Seiten eingerichtet, die zur externen Kommunikation dienen. Hier werden die Arbeiten der Schüler laufend veröffentlicht und aktualisiert: ‘Virtuelles Klassenzimmer’. Daß dieses Angebot von den Maple-Usern in der Welt genutzt wird, zeigen die Server-Statistiken. Im Februar 1998 haben allein auf den BelWue-Server im Maximum 600 Besucher pro Tag zugegriffen und 11000 Dateien angefordert (etwas kleinere Zahlen beim FH-Server, auf dem ältere Beiträge verfügbar sind). Etwa ein Viertel der Anfragen bezog sich auf Maple-Dateien.
Die Pflege von WWW-Seiten (Dateitransfer mit FTP und Aktualisierung der Links) ist von einem einzelnen Webmaster bei diesem Volumen nicht mehr durchführbar. Deshalb wurde ein schuleigener Datenbank-Server (Lotus Notes Domino) frühzeitig konzipiert und so eingerichtet, daß ‘er sich selbst pflegt’, d.h., die Abgabe, Aktualisierung, Einordnung, Recherche und zugehörige Kommunikation wird nicht mehr zentral von einem Administrator durchgeführt, sondern dezentral von jedem Benutzer selbst. Dadurch ist gewährleistet, daß das Vorhaben Telelearning auch skalierbar bleibt. Dem Administrator des Servers bleibt immer noch genug Arbeit, mit der Gesamtkoordination und Weiterentwicklung.
Diese technischen und organisatorischen Vorkehrungen bilden die Grundlage für Telelearning schlechthin. Ihre Realisierung hat einige wichtige Erkenntnisse für die Praxis geliefert (siehe gesonderter Bericht...). Unter dem Aspekt ‘Verwaltung’ sollte aber noch erwähnt werden, daß ein Projekt dieser Größenordnung nur von einer Mannschaft getragen werden kann. Alle oben genannten Tätigkeiten und Aufgaben werden deshalb von speziell dafür ausgebildeten Schülern übernommen (seit dem Schuljahr 97/98 zum Teil auch Schüler aus einem vorgezogenen Seminarkurs). Dies unterstreicht ein weiteres Mal, wie man mit den neuen Technologien auf natürliche Art Schüler zu den viel zitierten ‘Schlüsselqualifikationen’ führen kann, hier insbesondere zur Verantwortung.
Der Weg zur neuen Mathematik führt über die Technik, oder wie es in unserer Zeit heißt über die ‘neuen Technologien’. Deshalb stehen die folgenden Abbildungen bewußt im Abschnitt Technik. Denn die Technik ist es, die den Strukturwandel ermöglicht und stellenweise auch erzwingt. Der neue Mathematikunterricht hat keine reine Blockstruktur mehr sondern wird vernetzt und kommt damit assoziativ und visuell denkenden Schülern sehr entgegen (siehe... ).
Die Vernetzung ist eines der wichtigsten Merkmale der neuen Technologien und zwar durchgehend - lokal und global. Hypertext ermöglicht die interaktive Nutzung von Querverweisen innerhalb eines Dokuments oder auf andere Dokumente auf dem selben Computer. Lokale Netzwerke ermöglichen den Zugriff auf Dokumente, die auf anderen Computern in einer kleineren Einheit (z.B. Schule) stehen. Globale Netzwerke verbinden lokale Netzwerke... Im Endeffekt kann von jedem Notebook aus auf alle Dokumente der Welt zugegriffen werden, die für diesen Zugriff freigegeben sind. In dieser vernetzten Welt werden unsere Schüler morgen geprüft werden, wenn sie die Klausuren unsere Schulen bestanden haben. Diese virtuelle Welt wird ihre reale Welt sein. Und darüber freut sich der Mathematiker, denn er sieht die Kongruenz zur mathematischen Welt mit all ihrem Reichtum, ihren Verflechtungen, Problemen, Schönheiten und... Trivialitäten. Die Technik hat die Mathematik eingeholt, es wird eine neue Mathematik entstehen. Eine neue Mathematik, an der jeder teilhaben kann und zu der jeder beitragen kann - virtuell.

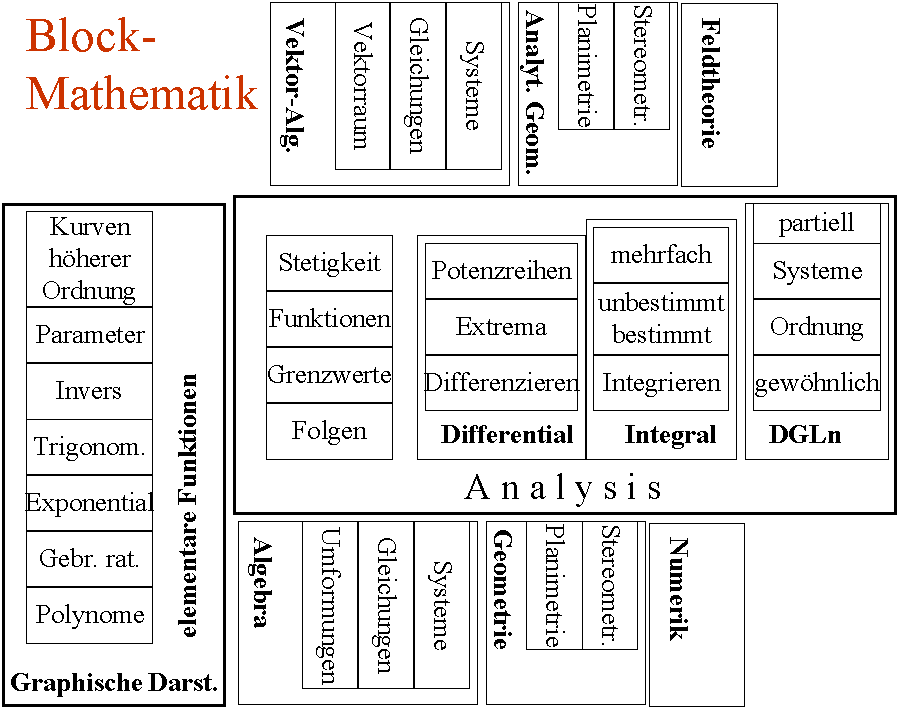
Abbildung 1 Die ‘Blockmathematik’ hat eine gute Tradition. Das Fach selbst ist wohl strukturiert und bietet eine Kategorisierung an. Der Lernende findet sich leichter zurecht, wenn er weiß, in welchem Teil des mathematischen Gebäudes er sich bewegt, und erwirbt so eher und zuverlässiger Fertigkeiten. Man kann aber die mathematischen Etüden auch übertreiben und den ohnehin beim Lernenden vorhandenen Hang zum Schubladendenken fördern, wenn man - wie in den meisten Schulbüchern - seitenweise Aufgaben stellt, die mit einem einzigen Ansatz gelöst werden können, der meist schon der Überschrift zu entnehmen ist. Umgekehrt ist es schwierig, mit den herkömmlichen Medien die durch die Struktur des Faches vorgegebenen Grenzen zu überspringen: Eine Unzahl von Querverweisen in gedruckter Form würde unnötig vom aktuellen Thema ablenken und die Orientierung erschweren, ganz zu schweigen vom hohen Aufwand beim Textsatz. Dadurch geht aber notwendigerweise in einem gedruckten Mathematikbuch der Beziehungsreichtum der Mathematik verloren. Der Schüler hat kaum eine Chance, Analogien zu entdecken und Assoziationen zu knüpfen, weil er (zumindest vom Buch) linear durch die Mathematik geführt wird. Natürlich wird ein guter Mathematiklehrer versuchen diesen Defekt der herkömmlichen Medien auszugleichen, aber das ist nur in engen Grenzen möglich, weil bei der nächsten Klassenarbeit eben Aufgaben dran kommen, die zum ebenso linear strukturierten Lehrplan oder einer linear strukturierten Abi-Aufgabe passen (Aufgabe I / 1 Analysis / Exponentialfunktion).

Abbildung 2 Das ‘Mathematische Netz’ ist die Mathematik schlechthin. Mathematik betreiben heißt nicht Konzepte abspulen - dazu haben wir inzwischen den Computer. Mathematik betreiben heißt Konzepte finden, Prinzipien finden und - sie beweisen (vielleicht haben wir auch dazu morgen den Computer). Der Mathematiker als Forscher weiß das. Aber für die meisten Didaktiker der Schulmathematik bedeutet das einen Paradigmenwechsel: Von der Fertigkeit zur Fähigkeit. Es scheint nun so, als würde dieser Paradigmenwechsel durch die neuen Technologien nicht nur ermöglicht, sondern sogar erzwungen. In einem elektronischen Mathematikbuch muß nur ein Hyperlink angeklickt werden, um zu einem verwandten Thema zu springen. Dabei muß das Ziel des Links nicht im gleichen Buch auf dem gleichen Computer liegen, es kann sich irgendwo auf der Welt befinden. Mit dieser Topologie muß die Didaktik der neuen Mathematik fertig werden. Viele Didaktiker schrecken vor dieser Aufgabe zurück und viele Mathematiklehrer bevorzugen einen Unterricht (und eine Korrektur von Klassenarbeiten), der innerhalb einer Schublade bleibt: Nur so könne der Schüler etwas lernen. Es ist auch in der Tat nicht problemlos, Schüler, die 10 Jahre lang linear und rezeptiv (mit Rezepten) unterrichtet wurden, mit der Vielfalt der Mathematik zu konfrontieren. Aber - das sei hier vorgreifend gesagt - es geht! Aus einem einfachen Grund: Die Jugend kommt mit dieser Topologie spielend und surfend zurecht.
Auch dieser Abschnitt steht bewußt (als letzter) im Technik-Kapitel. Er soll zur Didaktik (eigentlich Pädagogik oder gar Politik?) überleiten. Ich kann aber in diesem Rahmen nur kurz streifen, welche Brisanz die Überschrift in sich birgt.
Vor kurzem sprach H.v.Hentig im Fernsehen (ZDF 29.1.98) von seiner Laborschule und betonte dabei besonders, daß in dieser ‘offenen Schule’ nicht hinter verschlossenen Türen unterrichtet wird. Genau das ist auch die didaktische Zielsetzung des ‘virtuellen Klassenzimmers’ am IKG. Aus einem einfachen Grund: die Neuen Technologien werden eben dies früher oder später bewirken, nämlich eine völlige Demokratisierung von Forschung und Lehre, manche befürchten sogar eine Art Anarchie. Es ist außerordentlich schwierig, das Für und Wider der derzeitigen technischen Entwicklung und ihre Auswirkung auf die Gesellschaft (und Moral) zuverlässig abzuschätzen. Dagegen ist es relativ einfach, zuverlässig zu prognostizieren, welche Fakten die neuen Medien und die Vernetzung schaffen werden. Auf dem elektronischen Markt, wird nicht nur mit Informationen gehandelt, nicht nur mit Daten (für Computerfreaks), sondern auch mit Geld und Waren - und Bill Gates weiß das, wenn er nun meint, der ideale Markt von Adam Smith sei zur Realität geworden (auf virtuellen Servern). H.v.Hentig scheint das auch zu ahnen, denn er sprach in besagtem Fernsehinterview nicht mehr von dem ‘Golem Computer’ wie früher, sondern sagte, daß er dafür (für den Computer) zu alt sei. Unsere Schüler sind es nicht. Sie wachsen in diese ‘vollständige Lernumgebung’ hinein - ob sie (oder wir) es wollen oder nicht. Ich denke nicht an heute und morgen, sondern an die nächsten 10 oder 20 Jahre. Und vor diesem Hintergrund und mit dieser Zielrichtung muß ein Pilotprojekt laufen: Wenn wir noch irgendwie steuernd Einfluß auf die sich zunehmend verselbständigenden Prozesse nehmen wollen, müssen wir gerade an den Schulen in Erfahrung bringen, was prinzipiell möglich ist. Das geht aber nur, wenn wir schon heute versuchen, die Situation von morgen zu simulieren, sei das nun Hentigs offene Schule oder das virtuelle Klassenzimmer (das man auch gläsernes Klassenzimmer nennen könnte). Es nützt aber nichts, einen pädagogischen Ansatz (oder ein Ideal) zu haben, der die Realität ignoriert, denn die Realität orientiert sich nicht mehr an Konzepten einzelner Pädagogen (leider?). Die technische Realität erhebt überall Anspruch auf Vollständigkeit. Sie ist zum ‘public eye’ geworden, das auch Hentig favorisiert. Sie ermöglicht eine ‘vollständige Lernumgebung’, die von multimedialen Programmen über Lernsoftware-Systeme bis zur Vernetztung reicht. Viele stemmen sich immer noch vehement gegen diese Horrorvision, die man auch in vielen Karikaturen sieht: Schüler, die einfach direkt mit der Maschine verkabelt sind: Gehirn - Computer. Und man zitiert Freud, der sich schon zu seiner Zeit Sorgen um einen Menschen gemacht hat, der sich mit immer mehr Prothesen umgibt. Der Fluch der Technik? Tabuisierung der Technik ausgerechnet von dem, der so viel enttabuisiert hat? Da hilft nur ein einfacher pragmatischer Ansatz: Die Technik ist da (nicht erst seit Aristoteles), Erfindungen lassen sich nicht verbieten und waren schon immer ambivalent. Also muß man lernen, mit der Technik umzugehen, sie zu beherrschen (und nicht die Natur).
Die Beherrschbarkeit ist ein Aspekt beim Umgang mit der Technik und mit vollständigen Lernumgebungen. Ein anderer ist die Ausschöpfung ihres riesigen Potentials. Auch hier möchte ich einen Artikel von Hentig mit der Computer-Realität konfrontieren. In einem Essay in ‘Psychologie Heute’ (Februar 98) zum ‘Mythos Kreativität - Der Kult um einen (be)trügerischen Begriff’ sieht man auf der ersten Seite eine der oben erwähnten Karikaturen des verkabelten Schülers - furchterregend, beklemmend (zumindest löst sie bei mir ein gewisses Unwohlsein aus). Man vermutet also zunächst eine weitere Verdammung oder Verunglimpfung der Technologien durch Hentig. Doch beim Lesen des Artikels stellt man bald fest, daß es diesmal gar nicht gegen den Computer geht, sondern gegen die ‘Kreativitäts-Didaktiker, die wie selbstverständlich von der kreativ-intuitiv-sinnlichen Komponente ihrer Arbeit sprechen, als sei das eine gegebene Einheit’. ‘Dieselben bekennen sich auch zu der Absicht, die Kinder dem Irrationalen und Verrückten gegenüber aufzuschließen’. Wird das durch die Karikatur symbolisiert? Der Computer als Symbol für Irrationales? Nein - die Computerkarikatur scheint hier nur gewohnheitsmäßig in das Layout gerutscht zu sein, vielleicht eine kleine Fehlleistung beim Satz des Essays. Der Computer wird diesmal wirklich nicht von Hentig gegeißelt, aber - zu Recht - die Kreativitätsdidaktiker, die ‘wissenschaftliche Anleitungen zum Querdenken geben’ und deren ‘pädagogische Planungsenergie beängstigend ist’. Das Essay schließt so: ‘Wo immer wir von der Kreativität ein Wunder erwarten, werden wir es nicht bekommen. Wir müssen das mühsamer werdende Geschäft der Politik, der Wirtschaft, der Wissenschaft, der Pädagogik weiterhin mit den großen alten Tugenden bewältigen und dürfen froh sein, daß es immer wieder die Glücksfälle der Hochbegabten, der Schöpferischen, der heiteren Hermeskinder gibt’ (und es folgt die Anmerkung der Redaktion, daß es sich bei dem Essay um einen Auszug aus einem Buch von Hentig handelt). Aber das sind doch Binsenweisheiten! Freilich hat Hentig recht, wenn er sie in Erinnerung bringt und vor Betrügern warnt, die nun wieder mit dem Nürnberger Trichter hausieren gehen - computergestützt. Nur fehlt nach dem Schlußsatz eine Empfehlung, ein wirklicher logischer Schluß, wie es denn nun weitergehen soll. Sollen wir Pädagogen die Hände in den Schoß legen und angesichts der massiven Verwerfungen, die auf allen Ebenen der Gesellschaft durch die technische Revolution ausgelöst werden, nur darum beten, daß uns genügend viele Glücksfälle beschert werden? Wenigstens den Versuch einer Planung sollten wir doch wagen bevor wir unsere didaktische Bankrotterklärung unterschreiben. Und so paradox es erscheinen mag - eben diese Revolution hilft uns bei der Planung. Aber es ist nicht die Planung vom grünen Schreibtisch eines Kreativitäts-Didaktikers oder Lernsoftware-Designers aus, da hat Hentig vollkommen recht. Es ist eine offene Planung, die flexibel genug ist, die Möglichkeiten einer ‘vollständigen Lernumgebung’, in die Praxis um zusetzen. Und das geht nur in der Praxis und nicht in Essays. Wir haben am Isolde-Kurz-Gymnasium schon erste Erfahrungswerte: Je mehr man dafür sorgt, daß die (neue) Lernumgebung vollständig wird, desto fruchtbarer wird der Boden für ‘kreative Glücksfälle’. Eigentlich auch eine Binsenweisheit, aber man muß das erst einmal mit den neuen Technologien konsequent in die Tat umsetzen. Mit der Kreativität und der Intuition ist das eben wie mit der kritischen Masse: Je mehr man zur Verfügung stellt, desto wahrscheinlicher klappt die Zündung. Die Planung besteht also fürs erste schlicht in der logistischen Aufgabe, für genügend Ressourcen zu sorgen, die es dem Schüler ermöglichen, sich ohne Bruch (Medienwechsel) in der neuen Lernumgebung zu bewegen. Aber die Planung besteht natürlich nicht in einer lehrplanartigen Anleitung zur Kreativität. Es ist Fakt, daß die neuen Technologien ein angenehmes Reizklima für Kreativität schaffen - das ist ihr Potential. Und wenn der erste Funke gesprungen ist, entwickelt sich eine Eigendynamik, die sich selbst steuert. Freilich nicht bei allen. Wer schon ohne Computer zur Oberflächlichkeit, Sprunghaftigkeit und Unrast neigte, wir diese schlechten (anerzogenen?) Gewohnheiten mit dem Computer verstärken - und so weiter für alle anderen negativen und positiven ‘Charaktereigenschaften’. Der Computer ist weder Heilsbringer noch Golem. Er ist ein Werkzeug, das wir in seinen Funktionen vervollständigen können (und werden). Das ist kein Alibi dafür, daß wir uns selbst nicht vervollständigen können - so wie es aussieht. Aber vielleicht ist das auch eine Chance: ‘der Computer’ fungiert nicht nur als Prügelknabe der Schreitisch-Didaktiker, er fungiert auch als Spiegel unserer Probleme und als Katalysator bei ihrer Lösung - so oder so. Wir sollten die großen alten Tugenden nicht vergessen. Oder heißt das nun Schlüsselqualifikationen in der vollständigen Lernumgebung?
5 Didaktik
Es ist nicht einfach, den aktuellen Stellenwert der Didaktik anzugeben, weil wir mitten in einer technischen Revolution leben, die überdies noch mit einer grundsätzlichen Debatte über die Didaktik der Mathematik oder sogar über den Sinn des gegenwärtigen Mathematikunterrichts an Schulen verquickt ist - nicht ohne Grund. Deshalb stimmt es um so bedenklicher, wenn nun die News-Group ‘mathe.did’ mangels Beteiligung geschlossen wurde: Gibt es im Netz kein Interesse für die Didaktik der Mathematik oder interessieren sich die Didaktiker nicht für das Netz? Aber vielleicht lassen sich diese Fragen so beantworten:
Auf der MNU-Lehrplantagung Mathematik 1995 begann der Didaktiker Helmut Heugl sein Referat (Vorstellung des österreichischen DERIVE-Projekts) etwa so: „Man sollte sich immer im klaren darüber sein, welche Faktoren mit welchem Gewicht zum Lernerfolg beitragen: Motivation 90%, soziales Umfeld (Klasse) 5%, Arbeitsmaterial 2%, Methode 2% und didaktische Konzeption 1%„. Das ist eine Einleitung, die noch mehr zu denken gibt als die Stillegung einer Kommunikationsmöglichkeit für Mathematikdidaktik, zumal wenn sie von einem erfolgreichen Didaktiker vorgetragen wird. Es mag etwas Understatement dabei sein und über Prozentzahlen läßt sich immer streiten. Bemerkenswert ist aber in jedem Fall die Relativierung der Konzeption - gerade in unserer Zeit der ‘Lernsoftware’, die manchmal wie ein neuer Nürnberger Trichter angepriesen wird - und die Betonung des rein psychologischen Faktors Motivation. Man müßte nun diesen Faktor weiter aufschlüsseln: Person des Schülers (privates soziales Umfeld), Interesse des Schülers am Stoff (Neugierde allgemein, aber auch die nächste Prüfung...), Person des Lehrers (und Motivation des Lehrers - ohne weitere Aufschlüsselung...), Wechselwirkungen der einzelnen Faktoren und vieles mehr. Alles Faktoren, die in keinem Lehrplan stehen (allenfalls in der Präambel angedeutet werden), ja die sich von Natur aus jedem didaktischen Konzept entziehen. Motivation kann nur in sehr bescheidenem Maß durch didaktische Konzepte unterstützt werden, das ist wohl der Kern des Heuglschen Vorworts. Pädagogisches Geschick kann da viel mehr erreichen. Nur pädagogisches Geschick?
Ich habe in diesem Projekt (und in seinem Vorfeld) erlebt, wovon ich immer geträumt habe (und die vielen Kollegen, die in einer ähnlichen Situation sind, berichten das übereinstimmend): Die neuen Technologien bewirken einen ungeheuren Motivationsschub! Wenn dann noch in einem Pilotprojekt das ‘Wir sind wer’-Gefühl dazu kommt, gibt es kein Halten mehr. Das ist keine kurzlebige Euphorie, das kann zum Dauerbrenner werden. Allerdings würde es beim Strohfeuer bleiben, wenn man dieser positiven Entwicklung didaktische Konzepte überstülpen würde oder auf Leitideen von gestern fixiert bliebe. Nichts wäre demotivierender (für alle Beteiligten), als der Versuch, eine fast alles revolutionierende Entwicklung in das Prokrustesbett überkommener Schemata und Schablonen einpassen zu wollen. (Ich denke dabei nicht nur an die Didaktik, sondern auch an die Verwaltung - auf allen Ebenen). Hier ist Kreativität gefragt! Schüler haben diese Kreativität von Natur aus - immer noch. Es gibt also für den Lehrer eigentlich nur eine didaktische Konzeption und Aufgabe: ‘Wie ermögliche ich es meinen Schülern, ihre Kreativität zu entfalten?’. Das ist aber in erster Linie eine pädagogische Aufgabe und nun (neue Technologien) auch vermehrt eine technische und organisatorische. Das ist mein zweites Projekt-Erlebnis: Der Rollenwechsel des Lehrers in unserer Zeit. Vielleicht macht er in der Statistik der Lernerfolgs-Faktoren auch nur ein Prozent aus, aber er hat eine zentrale Funktion der Steuerung, und deshalb habe ich ihm fast 100% meiner Zeit gewidmet. Der Rollenwechsel vom frontal unterrichtenden Lehrer zum ‘Moderator’ fiel mir nicht schwer. Die Installation der Software mit all ihren Updates haben mir in zunehmendem Maß kompetente Schüler abgenommen (ich mußte ihnen ‘nur’ die Möglichkeit dazu geben), und das Schreiben von Projektanträgen ist nun auch schon fast zur Routine geworden.
5.1 Stoffverteilung
In den einzelnen Stoffverteilungsplänen, siehe Anhang (...), ist nicht jede Stunde einzeln kommentiert. Das hat mehrere Gründe:
Der Schwerpunkt des Projekts am IKG liegt nicht bei fachdidaktischen Details der Mathematik sondern bei dem Versuch, den Computer als Hauptmedium im Unterricht einzusetzen.
Die wichtigste Erfahrung aus meinem Unterricht mit CAS in den Klassen 11 bis 13, die ich schon in den drei Jahren vor dem ‘Mobilen Klassenzimmer’ machen konnte, lautet: Flexibilität! Das heißt, es erscheint mir nicht sinnvoll, für eine bestimmte Unterrichtseinheit eine bestimmte Methode zu empfehlen, denn es läßt sich gerade mit einem CAS auch immer die umgekehrte Methode begründen (vgl. Heugls Black-Box / White-Box).
Die Reduktion des Unterrichts mit CAS auf den bestehenden Lehrplan würde nach drei Jahren CAS-Kursen keine wesentlich neuen Erkenntnisse bringen. Daß sich der Unterrichtsgang dennoch relativ eng an bekannte Themen hält, ist das Ergebnis der Forderung nach einem ‘Stoffkorridor’ und vor allem einer zentral gestellten Abituraufgabe.
Deshalb sind die charakteristischen Merkmale des Unterrichts mit CAS von der Stoffverteilung getrennt zusammengefaßt. Aber ob nun CAS-charakteristisch oder nicht, hinter allen Überlegungen zur Modernisierung des Unterrichts steht immer wieder die Frage nach dem Sinn des (Mathematik-) Unterrichts. Dieser immer währende Kampf von Tradition und Innovation wird ein weiteres Mal in einem Artikel in Newsweek Dez. 97 beschrieben: ‘Subtracting the New Math’. In Californien kehrt man wieder zu den Quellen zurück. Weil die Schüler angeblich nicht mehr Kopfrechnen können, fordern die Eltern wieder die ‘alte Mathematik’, damit sich ihre Kinder im Berufsleben zurechtfinden.
Übertragen auf unsere Projekte ist das aber auch ein Kampf um die Priorität von Inhalt und Methode. Er tritt nun verschärft beim Einsatz von Computern zu Tage, weil es bis heute noch Mathematiker und vor allem Mathematikdidaktiker gibt, die die Informatik aus der Mathematik verbannen wollen. Dabei ist es schon fast eine Binsenweisheit und muß doch immer wiederholt werden: Mathematik mit CAS setzt solide CAS-Kenntnisse voraus. Ein Vergleich aus dem musischen Bereich: Kein Geigenlehrer läßt seinen Schüler Mozart spielen, bevor dieser nicht die dazu notwendige Technik beherrscht. Das Instrument will gelernt sein, wenn aus der Kunstfertigkeit Kunst werden soll, erst recht, wenn es um eine Stradivari (= Laptop+Maple) geht. Man hört immer wieder von dem Frust, den CASe erzeugen können (bei Schülern und Lehrern), wenn sie zum ‘Lösen von Problemen per Knopfdruck’ eingesetzt werden.
Oder: Man kann schon mit einer sehr einfachen Mathematik sehr große Probleme mit Maple bekommen (komplexes System). Also ist Sicherheit im Umgang mit Maple gefragt. Möglichst viele Fehler und Fehlbedienungen sollten vor der (ersten) Klassenarbeit mit Maple vorgekommen sein. Nur so können die Schüler eine Überlebensstrategie entwickeln, die sie in Klassenarbeiten oft dringend benötigen (Bsple siehe...)
Es wäre ein falscher Ansatz, den alten Lehrplan und Prüfungen im alten Stil beizubehalten und das Notebook nur als komfortablen Taschenrechner, der nur additiv eingesetzt wird, zu verwenden. (Siehe Schwellen...).
Es gibt also eine Reihe von Problemen, wenn man von der Planung zur Praxis übergeht. Unsere Praxis am IKG sieht so aus (wobei ich nur die entscheidenden Punkte hervorhebe):
5.1.1 Das Werkzeug
Man beginnt naturgemäß mit der
Einführung in die Bedienung des Rechners und Windows:
In der ‘normalen Klasse’ mußte etwa die Hälfte der Schüler mit den elementaren Handgriffen und Strukturen vertraut gemacht werden. Zeitbedarf etwa 4 Wochen (parallel zum Mathematikunterricht), minimiert durch die tatkräftige Hilfe der zweiten Hälfte der Klasse, die sich gut bis sehr gut mit Windows (und bald auch mit dem Rechner) auskannte.Einführung in das CAS Maple: Es gehen Horrorgespenster unter den Mathematikern und den Didaktikern der Mathematik um. ‘Maple-Befehle auf Vorrat’, ‘für die Schüler unverständliche Befehle’, ‘Invasion der Mathematik durch die Informatik’, und was sonst noch an die Wand gemalt wird. Umgekehrt favorisieren eben diese Schreckhaften dann Prinzipien wie ‘Black-box / white-box’ die nichts anderes besagen (wie Heugl richtig ausführt), als daß man es dem Schüler zumuten kann, mit Wissenslücken zu leben (schließlich muten wir alle uns das ja jeden Tag zu). Wir haben deshalb von Anfang an folgendes vereinbart:
Zunächst beschäftigen wir uns mit der Sprache Maple so lange, bis wir sie (und die Fehlermeldungen) sicher beherrschen. Wir begnügen uns zu diesem Zweck mit einfachen mathematischen Fragestellungen.
Zum Zweck der Veranschaulichung und Begriffsbildung können auch vom Lehrer vorgegebene Maple-Passagen (Befehle) vorkommen, die erst später verstanden werden können (wenn wir die Sprache besser beherrschen). Diese Passagen werden (obwohl sichtbar) als Black-box behandelt und später ‘geöffnet’.
Und das funktioniert! Es funktioniert sogar so gut, daß die Schüler einfach durch Gewöhnung lernen, CAS-Befehle ‘mit denen sie nichts anfangen können’ einerseits zu ‘übersehen’, andererseits aber richtig auszuführen und sogar zu modifizieren. Sie lernen Strukturen erkennen (meistens durch trial and error) und das ist weit mehr als das Drücken eines Knopfs auf dem Taschenrechner (welcher Schüler - und Lehrer - weiß schon was sich in diesem Moment alles im Taschenrechner abspielt, in der Hard- und Software?). Dennoch liegt hier die zentrale Aufgabe für die Didaktik der Mathematik (mit CAS) von morgen (vgl. Kapselung..., vollständige Lernumgebung..., programmiertes Lernen...)
Schon an dieser Stelle läßt sich also als wichtiges Ergebnis festhalten:
Zu Beginn des Unterrichts mit CAS muß ein solides Grundwissen im Umgang mit der Sprache geschaffen werden. Dies darf nicht verwechselt werden mit einer übertriebenen Anhäufung von ‘Befehlen auf Vorrat’.
Es ist sicher sehr zweckmäßig, in Zukunft die Sprache eines CAS statt Pascal als erste Programmiersprache in ITG einzuführen. Dadurch könnte man in der Oberstufe praktisch nahtlos (Schüler und Lehrer) in den Mathematikunterricht mit CAS einsteigen.
5.1.2 Mathematische Inhalte
Die Unterrichtsgegenstände in den Klassen 11 bis 13 lassen das Herz eines jeden Mathematiklehrers höher schlagen: Spätestens hier kann man Schülern zeigen, wie Mathematik das Denken schult, und wie der Beziehungsreichtum dieses Faches zu vernetztem und assoziativem Denken motiviert. Der Dreh- und Angelpunkt ist dabei der Einstieg in die Analysis (siehe mathematische Landschaft...) und damit auch in die analytische Geometrie und (im Mathematikunterricht von morgen) in die Differentialgeometrie. Das oberste Ziel des Mathematikunterrichts in der Oberstufe ist es also, diese Ästhetik zu vermitteln. Man sollte auch versuchen, einem Gymnasiasten das ‘Wunder der Naturwissenschaften’ begreiflich zu machen: Wir (besser die Genies Newton, Leibniz, ...., Einstein, ..., Feynman,...) haben Formeln gefunden, die es uns erlauben, die Natur zu berechnen! Gab es diese Formeln schon immer?
Vor diesem Hintergrund, der gleichzeitig globales Ziel ist, muß die Mathematik in der Oberstufe unterrichtet werden: Warum funktioniert das alles so? Gibt es einfache Regeln? Wie bekommt man den Überblick?
Der Physiker oder Forscher (z.B. Newton und Feynman) denkt hier praktisch (‘anwendungsorientiert’): Wenn wir etwas Neues nicht genau kennen, so müssen wir ‘es annähern’. Unsere Näherung wird um so besser sein, je weniger wir uns von dem Bekannten entfernen. Um auf das Neue schließen zu können, benötigen wir einen (minimalen) Anhaltspunkt, wie es sich aus dem Alten entwickelt, eine Angabe über die Änderung. Sobald wir diese Angabe besitzen, können wir zumindest linear extrapolieren. Auf diesen ‘einfachen’ Überlegungen basiert ein Großteil unserer Naturwissenschaft: Näherung erster Ordnung, Näherung zweiter Ordnung, Näherung in höherer Ordnung. Und das wird auch so lange so bleiben, bis jemand die Weltformel gefunden hat. Bis dahin müssen wir uns damit begnügen, Näherungen zu verfeinern. Und dabei hilft uns die Idee, daß man Näherungsverfahren wiederholen kann, und... der Computer.
Aber das beste Verfahren und das beste Werkzeug helfen nichts, wenn man es nicht verständlich machen kann. Es gibt aber gerade unter den Physikern einen Mathematiker, der es wie kein anderer beherrscht, jemandem das notwendige Handwerkszeug beizubringen und das ist kein geringerer als der große Feynman. Wer das didaktische Naturtalent Feynman gelesen hat, sieht die Natur und die Mathematik mit anderen Augen. Das liegt an seiner Kunst zu elementarisieren ohne zu trivialisieren. Und ein elementares Mittel in der mathematischen Physik ist die ‘Näherung in erster Ordnung’ oder lineare Approximation:
5.1.2.1 Lineare Approximation
So oft sich die Gelegenheit dazu bietet - wenn ich nämlich eine 11. Klasse in Mathematik und Physik parallel unterrichten kann - pflege ich die gute alte Tradition, die Infinitesimalrechnung mit Hilfe der linearen Approximation einzuführen. Zufällig bekam ich auch ‘Das mobile Klassenzimmer’ für einen längeren Zeitraum vertretungsweise in Physik und wir entwickelten den Ableitungsbegriff nicht aus dem ‘Tangentenproblem’, sondern aus der stückweise gleichförmigen Bewegung, bei der die Geschwindigkeit eine Treppenfunktion ist. Bei diesem Zugang sind Stammfunktion (Weg) und Ableitung (Geschwindigkeit) von vornherein ein Funktionspaar, das auch beim Grenzübergang simultan behandelt wird. Das Ableiten und Integrieren wird nicht auf zwei Schuljahre verteilt, sondern ist von Anfang an eine logische Einheit (freilich steht in Klasse 11 zunächst das Ableiten im Vordergrund). Obwohl es sich um ein klassisches Vorgehen handelt, läßt sich gerade an diesem Thema zeigen, welche didaktischen Innovationen durch ein CAS möglich werden, ja dieses Thema ist geradezu das Paradebeispiel für einen Mathematikunterricht, der nur mit einem CAS so gemacht werden kann - und zwar auf verschiedenen Ebenen:
Visualisierung: Das Funktionspaar kann mühelos realitätsnah und exakt in vielen Variationen dargestellt werden. Besonders in Animationen wird der Grenzübergang sichtbar. Und bereitet über die Vorstellung eine Art der Begriffsbildung vor, wie sie mit herkömmlichen ‘toten’ Medien nie zu erreichen ist.
Experimentieren: Das CAS verarbeitet ‘beliebige’ Funktionspaare. Ohne Kenntnis der Ableitungs- und Integrationsregeln kann der Schüler alle Funktionen, die er bisher kennengelernt hat ‘durchtesten’. Dies fördert das Abstraktionsvermögen nachhaltig, weil sich der Schüler auf das Thema konzentrieren kann, ohne durch Rechenfehler oder zeitaufwendiges Zeichnen abgelenkt zu werden.
Übung und Kontrolle: So wie man bisher mit einem Taschenrechner etwas nachrechnen konnte, kann man mit einem CAS nun etwas symbolisch nachvollziehen. Egal welche Aufgabe gestellt wird, das CAS liefert die Lösung (zukünftige Mathematikbücher werden also keine Lösungen mehr enthalten, in denen die Ergebnisse zu Aufgabe 1 bis 17 stehen: diese Ergebnisse werden nun dynamisch (interaktiv) erzeugt). Dazu kommt, daß ‘Übung und Kontrolle’ bei der Arbeit mit einem CAS immer wechselseitig und mehrschichtig abläuft. Einfaches Beispiel: Man berechnet eine Ableitung von Hand und kontrolliert sie mit dem CAS oder umgekehrt.
Mathematisierung: ‘Saubere’ Definitionen und Sätze können mit einem CAS besonders schön erarbeitet werden. Das reicht von dem schnell verfügbaren Gegenbeispiel über die gut strukturierte Formulierung im Textteil bis zu CAS-gestützten Beweisen, in denen die Logik nicht zu kurz kommt. Aber auch ein ‘Blick hinter die Kulissen’ kann (für Fortgeschrittene) lehrreich sein: Wie berechnet Maple die Ableitung? Wer sich Maple-Prozeduren einmal anzeigen läßt, sieht die Vorstufe zur künstlichen Intelligenz.
5.1.2.2 Kurvendiskussion
Die im CAS-Zeitalter etwas in Verruf geratene Kurvendiskussion ist selbst eine Anwendung, an der sich viel lernen läßt - gerade mit einem CAS. Zunächst steht wieder die bis dahin nie gekannte Anschaulichkeit im Vordergrund. Funktionen werden für die Schüler zu ‘begreifbaren Wesen’: Besonders beeindruckend ist in dieser Hinsicht, daß man nun in Maple V Release 5 einen Funktionsterm mit der Maus in ein Plotfenster ziehen kann, wo er sich in eine Kurve verwandelt. Umgekehrt kann man eine Kurve aus einer Zeichnung auswählen und in den zugehörigen Term verwandeln. Nimmt man noch die Animation hinzu, so wird die Formulierung ‘begreifbare Wesen’ klar. Ich kann mir wirklich keine engere Bindung abstrakter Term - reales Bild vorstellen. Hier erweist sich das CAS den herkömmlichen Methoden als haushoch überlegen und eignet sich hervorragend zur Schulung beim Erkennen und Kennenlernen von Funktionen. Schließlich sollte man auch nicht die Ästhetik vergessen. Es ist einfach schön, Kurven zeichnen zu können, die nicht verwackelt und eckig sind. Auch der ungeschickte Schüler hat nun die Möglichkeit, Kurven zu zeichnen die an sich schön sind und wird dadurch seinerseits animiert, das Zeichnen auch von Hand zu üben.
Es ist auch nicht ganz richtig, immer wieder darauf abzuheben, daß die Kurvendiskussion mit einem CAS sinnlos wird. Zuerst muß ja ein Worksheet geschrieben werden, daß möglichst mit allen Termen fertig wird. Und da lassen sich die Ansprüche an die Programmierfähigkeit der Schüler leicht sehr hoch schrauben! Und wer dann so ein Universal-Worksheet geschrieben hat und damit umgehen kann, der hat mit Sicherheit verstanden, was Kurvendiskussion bedeutet.
Extremwertaufgaben sind nach wie vor ein gutes Feld für Anwendungsaufgaben (es muß ja nicht ausgerechnet die viel strapazierte Milchtüte sein), das sich an das Thema Kurvendiskussion anschließt. Man kann aber auch an Variationsaufgaben denken (siehe...).
5.1.2.3 Kurvenscharen
Auch dieses Thema bleibt als solches interessant und kann mit einem CAS wie im konventionellen Unterricht behandelt werden. Aber neben den oben genannten CAS-spezifischen Möglichkeiten lassen sich anhand dieses Themas zwei weitere Merkmale eines CAS-gestützten Unterrichts gut darstellen, die im konventionellen Unterricht nie möglich sind.
Vernetztes Denken: In der Mathematik gibt es Themen, die wie Knoten in einem Netz fungieren. Besonders interessant sind dabei Knoten, an die viele Beziehungen geknüpft sind und bei den Kurvenscharen handelt es sich um einen solchen Hauptknoten. Man kann nun mit Hyperlinks diese Vernetzung nachbilden, indem man Worksheets verknüpft, die mit Scharen zu tun haben: Scharen als solche, Übergang ins Dreidimensionale, gemeinsamer Punkt, Ortskurven, Isoklinen, Orthogonaltrajektorien, Scharen als Integralkurven, Scharen und Differentialgleichungen, Richtungsfelder, Feldlinien, Felder in der Physik, parametrisierte Felder... Das läßt sich in keinem gedruckten Buch machen. Mit einem hypertextfähigen CAS ist es aber eine einfache Übung, die überdies vom Schüler selbst noch interaktiv verändert werden kann. Sicher fällt es zu Beginn dem Neuling, der sich die Struktur ja erst erarbeiten muß, nicht leicht, mit der Informationsfülle und der großen Zahl von Möglichkeiten fertig zu werden. Aber schon nach kurzer Zeit, ‘wenn der erste Pfad durch den Dschungel gebahnt ist’, erleichtert gerade diese Informationsfülle Assoziationen und schult sie. Vielleicht ist das sogar das Wichtigste: Es gibt keine Anleitung dazu, wie man eine ‘Idee hat’, aber man kann den intuitiven Sprung erleichtern, nahelegen.
Mathematisches Universalwerkzeug: In der Mathematik gibt es Themen, die im Prinzip jeder Elftklässler verstehen kann, die aber bis heute an der Schule Tabu waren, weil sie für Schüler nur in trivialen Fällen ‘von Hand’ lösbar sind. Eins davon sind die Differentialgleichungen. Sie sind ein wichtiges Thema in den Naturwissenschaften und ein Thema, das immer mit einer Vielfalt von Funktionen zu tun hat: ‘Differentialgleichungen erzeugen Scharen’. Eine Schar ohne Differentialgleichung ist ganz schön, aber man weiß nicht, woher sie kommt und mußte es bis heute auch immer ‘geheim halten’. Ganz anders mit einem CAS: Man hat den Befehl ‘dsolve’ und schon ist die DG gelöst und eine neue Schar produziert, die obendrein noch eine wichtige Rolle bei der Lösung eines Problems oder bei einer Modellierung spielen kann. Es gibt keinen besseren Anwendungsbezug für den Ingenieur und den Architekten von morgen, aber auch für den Biologen und den Ökonomen tut sich hier ein reichhaltiges Betätigungsfeld auf. Von der analytischen Lösung kann man noch zu numerischen Methoden übergehen, alles mit diesem Universalwerkzeug CAS, aber undenkbar in einem konventionellen Unterricht.
5.1.2.4 Integralrechnung (in Klasse 11)
Der Hauptzweck der Integralrechnung ist das Lösen von Differentialgleichungen (schon seit Newton). Warum unterrichtet man das dann nicht so, sondern verwendet die Integralrechnung an der Schule fast ausschließlich dazu, Flächen und Volumina zu berechnen? Warum unterrichtet man diese Pseudo-Anwendung, die in der Praxis fast nicht vorkommt, weil man nur höchst selten eine ‘krummlinig begrenzte Fläche’ hat, deren Grenze als Funktion gegeben ist, sondern eher Meßdaten, die man zur numerischen Integration verwendet? Mit aus dem oben genannten Grund: Das Lösen von Differentialgleichungen kommt bis heute erst etwa im vierten Semester eines naturwissenschaftlichen Studiums dran. Nicht mehr! Der Befehl ‘dsolve’ macht das nun schon in der elften Klasse. Die Rechenhürde ist weg und die Struktur wird sichtbar: ‘so funktioniert die Natur und so läßt sie sich durch DGLn beschreiben!’ (Vgl. ‘Newtons Maschine’ in Mod. Phys. mit Maple, Komma.) Dabei ist zu betonen, daß man mit einem CAS im Gegensatz zu fertigen Modellbildungssystemen wesentlich näher an der Mathematik arbeitet, die hier nicht in black boxes versteckt wird wie etwa in den Symbolen von Programmen wie Modus, die freilich auch ihre Vorteile haben (z.B. beim Einstieg in die Problematik).
5.1.2.5 Folgen und Grenzwerte (Leistungskurs 12)
Zur gedanklichen Durchdringung der Infinitesimalrechnung mit all ihren Facetten (von der simplen Nullfolge bis zur Mandelbrotmenge): Dies ist wieder ein Paradebeispiel für einen Mathematikunterricht der nur mit einem CAS so zu machen ist, und der auch erheblich mehr bringt als ein konventioneller Unterricht zu diesem Thema. Ich kenne nur wenige Mathematiklehrer und Schüler, die dieses Thema in einem Tafelunterricht bisher genossen haben. Es zählte von je her zu den trockensten Themen der Schulmathematik - etwas für echte Mathematiker, die sich durch alles durchbeißen (was im Lehrplan steht). Diese Zeiten sind nun vorbei, denn ein CAS ermöglicht:
Bequeme Ausgabe von Zahlenfolgen (ohne jede Programmierung, es reicht der Befehl ‘seq’).
Zeichnen von Punktefolgen.
Experimentelle Mathematik: ‘Man sieht den Grenzwert’ den Zahlen und Punkten an, man stellt eine Vermutung auf und beweist sie.
Begriffsbildungen wie Häufungspunkt und Grenzpunkt entstehen alleine durch das Hinschauen.
In Referaten können komplexe Folgen behandelt werden.
Beweise (z.B. vollständige Induktion) können programmiert werden, endlich hat Schulmathematik etwas mit Logik zu tun und wenn man dem CAS in die Karten schaut, wird wieder ein Zipfel der künstlichen Intelligenz sichtbar, den hinter dem Unterricht mit einem CAS steht ja immer die Frage: 'Wie schafft es diese Maschine, etwas symbolisch zu berechnen oder gar zu beweisen, worüber sich ein normaler Sterblicher (aber auch ein Schachweltmeister) ziemlich lange den Kopf zerbrechen muß?’ Wie hat man ihr all die notwendigen Fallunterscheidungen beigebracht? Welche Fallunterscheidungen und Schlußfolgerungen sind überhaupt notwendig, um eine gestellte Frage zu beantworten? Auch und gerade aus diesem Grund sei noch einmal betont, wie wichtig es ist, die Sprache des CAS zu beherrschen. Nur so kann man begreifen, wie hier Denken abgebildet wird, um dann an diesem Abbild wieder die Mathematik zu erkennen. Ich kenne keinen Lehrer, der bereit wäre, sein Gehirn für diesen Unterrichtszweck sezieren zu lassen. Aber ich kenne ein System, das sich bereitwillig bis in seine letzten Bestandteile zerlegen läßt: CAS.
5.1.2.6 Gebrochen rationale Funktionen
Von der Folge zur Funktion, vom Diskreten zum Kontinuum. Unter diesem Motto gelingt mit einem CAS (aber auch an der Tafel) leicht der Übergang zum wichtigen Thema der gebrochen rationalen Funktionen. Aber nur mit einem CAS lassen sich die zentralen Fragestellungen wie Konvergenz, Divergenz und Asymptotik so behandeln: Ohne Kenntnis von irgendwelchen Ableitungsregeln. Das eigentliche Thema steht im Vordergrund der Schüler muß sich nicht mit der üblichen Lawine von Rechenfehlern bei der Quotientenregel plagen, er nimmt einfach den Befehl, den er schon immer genommen hat, wenn er eine Funktion ableiten wollte, oder die Befehlsfolge, die er schon immer genommen hat, wenn er einen Wendepunkt gesucht hat. Freilich bleibt er von den Ableitungsregeln nicht verschont. Im Gegenteil: Es dauert nicht lange und er will sie von sich aus wissen, weil er sich wundert, weshalb das alles so schön funktioniert. Da ist sie wieder die experimentelle Mathematik! Nichts motiviert so stark wie die Neugierde. Also werden die Ableitungsregeln nachgereicht, symbolisch mit Hilfe des CAS (nach entsprechenden Vermutungen). Wie kann man sie beweisen? Mit der linearen Approximation! Von Hand und mit dem CAS. Und nun müssen die Regeln natürlich internalisiert werden: Übungen von Hand, Kontrolle mit dem CAS - eine unendliche Aufgabensammlung mit einem ebenso mächtigen ‘Lösungsheft’ steht zur Verfügung.
5.1.2.7 Integralrechnung (Leistungskurs 12)
Nachdem nun die Folgen behandelt wurden und auch schon Reihen vorkamen, ist es an der Zeit, den Integralbegriff als solchen zu vertiefen und zu ‘mathematisieren’: Summendefinition. Welcher Lehrer kann Ober-, Unter- und Zwischensummen zu beliebigen Funktionen als Animation darstellen und gleichzeitig die zugehörigen Flächeninhalte auf 20 Stellen genau angeben, so daß man den Grenzwert leicht errät? Welcher Lehrer kann diesen Grenzwert für beliebige Funktionen sofort angeben? Nur der Lehrer, der ein CAS als zweite Autorität in seinem Unterricht akzeptiert. Und das sollte jeder Lehrer den Schülern zu liebe tun, denn diese zweite Autorität hat noch weitere angenehme Eigenschaften: Sie läßt sich in ein Notebook packen, mit nach Hause nehmen und zu jeder Zeit an jedem Ort befragen (wenn der Akku voll ist).
Anknüpfend an die lineare Approximation in 11, Abrundung der Integralrechnung, Ausblick: Kurvenintegrale...
5.1.2.8 Weitere Funktionen aus Reihenentwicklung
............
5.1.2.9 Reihen als solche
....................
Zwischenergebnis zu 'Mathematik im Netz':
Mit dem CAS und Hypertext haben wir die Möglichkeit, Mathematik so zu unterrichten, daß von vornherein die Struktur der Analysis komplett sichtbar wird. Diese totale Transparenz würde den Schüler überfordern - er würde ins kalte Wasser geworfen. Andererseits nähern wir uns so dem gläsernen Klassenzimmer.
Es hat sich aber in unserem Schulversuch gezeigt, daß die Schüler durchaus in der Lage sind, sich in diesem mathematischen Netz zurechtzufinden, ja daß dies sogar zu Abenteuerreisen ermuntert. Nur muß der Lehrer Geduld haben und darf nicht auf sofortige Umsetzung drängen. Der Lehrer kennt ja die Mathematik, das Reiseziel und die möglichen Wege schon (mit Papier und Bleistift und mit CAS). Er muß dem Schüler Zeit lassen, diese Pfade zu finden.
5.2 Unterrichtsformen und Methoden
Dieser Bericht mag vielleicht an manchen Stellen den Eindruck erwecken, daß man alles mit dem Computer machen müsse, was mit dem Computer gemacht werden kann. Aber so wurde natürlich nicht unterrichtet. Wir haben nur versucht, möglichst alles konsequent auszutesten, was wir im Rahmen unseres Projekts mit dem Computer machen können und was nicht. So ergab sich ziemlich bald ein Zeitverhältnis von 2:1 für die Arbeit mit bzw. ohne Computer, sowohl in der Schule als auch zu Hause. In Klasse 11 hat es sich als sehr vorteilhaft erwiesen, daß Herr Schlipphak eine Stunde pro Woche mit unterrichtete, so daß wir die gerade in der Startphase häufig auftretenden Bedienungsprobleme (Hardware und Software) recht gut in den Griff bekamen.
5.2.1 Wochenthemen
Der typische Ablauf einer Unterrichtswoche hat sich nun so eingespielt: Es wird ein für alle verbindliches Thema ausgegeben, das etwa eine oder zwei Wochen lang behandelt wird. Je nachdem, ob es sich dabei um ein völlig neues Thema handelt oder um die Fortführung eines bekannten Themas mit Aspektverschiebung, kann man unterschiedlich vorgehen. Bei neuen (vom Lehrer gestellten) Themen ist es immer noch am zeitsparendsten und effektivsten, wenn der Sachverhalt zunächst konventionell an der Tafel erörtert wird, in einer Art Lagebesprechung oder als Brainstorming. Aus dieser Besprechung ergeben sich dann Planungsansätze für die selbständige Bearbeitung durch den Schüler. Dann folgt die eigentliche Arbeitsphase, in der (meistens aber nicht zwingend) das Thema am Computer von den Schülern individuell oder in Gruppen bearbeitet wird. In dieser Phase fungiert der Lehrer als Berater und sorgt dafür, daß der Stand der Arbeiten nicht zu stark divergiert. Abschließend wird das Thema in einer Stunde besprochen, und zwar meistens von Schülern, die ihre Ergebnisse (Arbeitsblätter) mit dem Projektor vorstellen. Dieser Abschluß dient gleichzeitig der Ergebnissicherung (im Computer oder Heft) und dem Austausch der Arbeitsblätter. Bei diesem eher klassischen Unterrichtsverlauf ist also die selbständige Arbeit ‘geklammert’ von einem zentral geführten Einstieg und Abschluß. Man stelle sich eine konventionelle Unterrichtsstunde auf eine Woche ausgedehnt vor: Einstieg (Problematisierung/Motivation), Lösung/Durchführung, Übungsphase, Ergebnissicherung.
Die zentral geführten Abschnitte (Klammern) lassen sich aber ebenso in die Mitte legen. Dies bietet sich an, wenn man es nicht mit einem grundlegend neuen Thema zu tun hat. Dann bekommen die Schüler einfach einen ‘Forschungsauftrag’ und arbeiten von Anfang an selbständig (‘schwärmen aus’). In der Regel entstehen dann Probleme, Fragen, aber auch Lösungen, die den Erklärungsbedarf laufend steigern und man trifft sich zu einer Lagebesprechung ‘auf halbem Weg’, die dafür sorgt, daß alle etwa auf den gleichen Stand kommen und bis zum Ende selbständig weiterarbeiten können.
Wie immer in der Didaktik kann man nicht zwingend argumentieren, wann welcher Ablauf gewählt werden muß. Es läuft vielmehr auf Mischformen hinaus, die sich meist auch aus der Situation ergeben (z.B. wird vor Klausuren die experimentelle Mathematik in den Hintergrund treten und die Eergebnissicherung und Übung mehr Bedeutung bekommen).
5.2.2 Referate
Parallel zu den Wochenthemen werden von den Schülern umfassendere aber auch speziellere Themen in Referaten behandelt. Diese Arbeitsform ist in der Mathematik die eigentliche didaktische Innovation, die durch das CAS ermöglicht und ausgelöst wird: Der Schüler schreibt einen Erörterungsaufsatz zu einem mathematischen Thema. Freilich wäre das auch mit Papier und Bleistift möglich (und man hätte es schon immer tun sollen - jedenfalls in der Kursstufe), aber hier kommen die CAS-spezifischen Merkmale besonders zum tragen:
Vollständige Textverarbeitung ermöglicht eine ansprechende und übersichtliche Form und Struktur.
Graphik ermöglicht Veranschaulichung.
Symbolisches Rechnen ermöglicht eine mathematisch korrekte Behandlung.
Bereits vorhandene Arbeitsblätter (lokal oder global) können eingebunden werden.
So wird der Schüler vom Konsumenten zu Produzenten und kann universitätsnah und vorwissenschaftlich arbeiten. Deswegen werden die Themen auch durchweg als offene Fragen gestellt und enthalten (zunächst) keinerlei Arbeitsanweisung. Der Schüler ist selbst für die Beschaffung von Information verantwortlich, wobei ihm sein Notebook, das LAN, das WWW, aber auch die Schulbibliothek, sein Buch und sein Heft zur Verfügung stehen. Die Themen können (und müssen manchmal) inhaltlich seinen Fähigkeiten angepaßt werden und reichen von Wiederholungen oder Zusammenfassungen von bereits Bearbeitetem bis zu Problemstellungen aus der höheren Mathematik, die sich ja nun mit einem CAS auch schon in Klasse 11 erfolgreich und selbständig von Schülern bearbeiten lassen (z.B. Differentialgleichungen oder Fraktale). Auf diese Weise erreicht man eine außerordentlich hohe Motivation und sehr gute Leistungen. Das hat auch folgende Gründe: Im Gegensatz zu Referaten in Papierform entwickeln Maple-Arbeitsblätter um so mehr eine Eigendynamik, je souveräner der Autor mit dem Universalwerkzeug CAS umgeht. Oft wirkt die erste Lösung eines Problems wie eine Initialzündung, die eine ganze Kette neuer Fragen aufwirft, die sich - und das ist wichtig - ‘sofort’ und interaktiv mit dem CAS beantworten oder weiter untersuchen lassen. Das berühmte Gegenbeispiel, mit dem man eine Vermutung widerlegen kann, ist in der Mathematik nirgends so schnell zu finden, wie mit einem CAS: Man probiert es aus, numerisch, symbolisch oder graphisch. Deshalb enthalten die Themen auch zunehmend Beweise oder jedenfalls Anregungen zur Verallgemeinerung und Abstraktion. Freilich darf man von Elftklässlern keine mathematischen Wunder erwarten. Aber hier fängt die Mathematik ja eigentlich erst an und es ist immer wieder auch für den Lehrer lehrreich, die verschiedenen Lerntypen zu beobachten und auch mit der gesamten Klasse zu diskutieren. Die Schüler entwickeln so ein Methodenbewußtsein von dem sie nicht nur hören, sondern das sie selbst erfahren. Das CAS an sich ist schon stark motivierend. Aber wenn man es behutsam angeht, kommt noch ein weiterer Motivationsschub hinzu: Webpublishing. Die Referate werden im Internet veröffentlicht (beim BelWue und auf unserem Datenbank-Server). Man muß das (insbesondere bei den Schülerinnen) behutsam angehen, weil es nicht jedermanns Sache ist, auch fehlerhafte und unfertige Produkte zu veröffentlichen. Aber hier kommen nun die Vernetzung und die neuen Kommunikationsmöglichkeiten zum Tragen. Wenn die erste Scheu abgelegt ist und der Lehrer nicht zu sehr auf Perfektion pocht, trauen sich auch die Schwächeren ‘ins Netz’, denn sie sehen ja die Produkte der anderen Teilnehmer, und so entsteht eine Worksheet-Werkstatt, in der im Prinzip jeder weltweit mitarbeiten kann. Die Klausur wird durch die Dynamik der neuen Technologien geöffnet und der Produktionsprozeß beginnt sich selbst zu regulieren, weil einer am Beispiel des anderen lernt.
Wenn man die abgegebenen Referate durchgeht, sieht man noch einmal den ganzen Fächer der individuellen Bearbeitungsmöglichkeiten (der übrigens auch aus dem Informatikunterricht bekannt ist): Der eine beginnt mit einem riesigen Inhaltsverzeichnis, arbeitet sehr viel mit Text und Layout und vergißt über der Form den Inhalt. Andere produzieren erst einmal eine Batterie von Plots ohne jeden Text. Der Programmierer-Typ versucht alles (auch Problemchen, die durch einfaches Nachdenken in kurzer Zeit und ohne CAS zu lösen wären) mit tief geschachteteln For-Schleifen zu ‘erschlagen’. Und der ‘geborene Mathematiker’ schreitet zielstrebig vom Einzelfall induktiv zur Lösung und Abstraktion, die er dann deduktiv auf eine erweiterte Fragenstellung anwendet. Es gibt aber noch eine interessante Beobachtung:
Gerade die Schüler, die man im herkömmlichen Unterricht wohl eher als mittelmäßig einstufen würde, entwickeln - sich selbst überlassen und mit genügend Zeit ausgestattet - ein erstaunliches Geschick, Probleme nicht nur zu lösen, sondern auch die Lösung verständlich und manchmal sogar didaktisch sehr geschickt darzustellen. Das kommt offensichtlich daher, daß sie sich die Lösung selbst erarbeitet haben und dann wissen ‘wo’s lang geht’. Dieses Erfolgserlebnis teilt man natürlich gerne mit.
Anmerkung zu den Stichwörtern Sozialformen und Sozialkompetenz: So wenig Steuerung wie möglich, so viel Unterstützung wie nötig. Keine Einteilung in Gruppen durch den Lehrer, kein Aufbrechen von intakten Gruppen und kein künstliches Mischen. Gruppenpuzzle ist übrigens äußerst unbeliebt (vgl. 'wissenschaftliche Anleitung zur Kreativität').
5.2.3 CAS-Methodik
Es bleiben noch Beobachtungen allgemeinerer Art, die generell die Arbeit mit CAS an der Schule betreffen. Sei es nun bei der Behandlung der Wochenthemen oder bei Referaten oder bei speziellen enger gefaßten Fragestellungen. Dabei sollte man CAS nicht mit herkömmlicher Lernsoftware verwechseln (siehe LEU...): Lernsoftware aber auch vollständige Lernumgebungen (und Fernstudium) sind eher dafür gedacht, Fertigkeiten auszubilden und Faktenwissen anzuhäufen (vgl. Spektrum Februar 98). Dazu wird der Schüler durch das Lernprogramm gesteuert. Das Gegenteil ist beim CAS der Fall: Der Schüler muß lernen, das Programm zu steuern, und zwar so, daß er damit ein (mathematisches) Problem löst. Allerdings läßt sich mit einem CAS auch eine ‘Lernumgebung’ aufbauen. Dies muß aber wieder durch den Benutzer (ggf. Lehrer) erfolgen. Das bedeutet im einzelnen:
Für den Unterricht mit einem CAS ist die Arbeit in einem Worksheet typisch, d.h., man arbeitet interaktiv mit einem selbständigen System, mit einer zweiten Autorität, aber auch mit einem Gehilfen. Und dieses Arbeiten (oder der Gebrauch des Werkzeugs) will zunächst einmal selbst gelernt sein. Dies geschieht aber ‘nach oben offen’ und in ständigem Wechselspiel mit dem mathematischen Problem, denn neue mathematische Fragen, können oft nur mit neuen Sprachelementen (oder neuen Packages) bearbeitet werden. Insofern handelt es sich um eine Doppelbelastung und der Lehrer hat dafür zu sorgen, daß sie in erträglichen Grenzen bleibt. Ein CAS ist zwar ein Ideenlieferant und ein Intuitionskatalysator, wenn man es beherrscht, aber auch gnadenlos und ohne jede Fehlertoleranz. Wenn man es nicht beherrscht, wird es zur unerschöpflichen Frustrationsquelle und zum Motivationskiller. Der Schüler muß beide Seiten kennenlernen und er muß wissen, wie er das Potential des Systems nutzen und ständige Fehlermeldungen meiden kann, besser noch, wie er sie interpretieren und beheben kann. Auch hier ist neben logischem Denken Methodenbewußtsein gefragt: Wie verfolgt man ‘einen Fehler’ in einem komplexen Worksheet zurück bis zu seiner ersten Ursache? Ist es ein Denkfehler, ein Syntaxfehler oder ein simpler Tippfehler? In diesem Zusammenhang muß der Schüler auch über gewisse einfache ‘Überlebensstrategien’ verfügen, die ihm z.B. bei einer Klausur (einer an sich nicht CAS-typischen Situation) weiterhelfen - auch unter Zeitdruck, mehr dazu siehe unten.
Für den Gebrauch im laufenden Unterricht und zu Hause ist hervorzuheben, daß bei der interaktiven Arbeit mit einem CAS eigentlich nur Mischformen der Arbeitsweisen auftreten, weil alles ständig verfügbar ist. Übungen und Übungsphasen sind nicht mehr prinzipiell isoliert von der Begriffsbildung sondern in den Gesamtablauf integriert (freilich müssen sie manchmal isoliert werden, um spezielle Fertigkeiten zu trainieren). Aber, wie nun hinlänglich bekannt, treten Rechenfertigkeiten in den Hintergrund. An ihre Stelle tritt die Fertigkeit im Umgang mit dem System: ‘Wie bringe ich das System dazu, daß es für mich rechnet, und wie mache ich das möglichst geschickt?’ Es ist bei weitem nicht so, daß man nun einen ‘Rechenknecht’ für sich einspannt und dadurch überproportional viel Zeit für die ‘eigentliche Mathematik’ und das Problemlösen erhält. Es handelt sich eher um eine Verlagerung der notwendigen Fertigkeiten, aber um eine sinnvolle. Ein CAS muß per se so strukturiert sein wie die Mathematik, die es zu betreiben erlaubt (die erwähnte Vorstufe zur künstlichen Intelligenz). Wird die Mathematik komplex und anspruchsvoll, so wird es auch die Bedienung des CAS. Weit verzweigte echte Fallunterscheidungen lassen sich nun einmal nicht durch eine Maschine simplifizieren, sondern müssen durch die Maschine nachgebildet werden. Aber hierin liegt gerade der Lerneffekt, der den Mathematikunterricht mit einem CAS so wertvoll macht. Man muß in erster Linie wissen, wie man es macht und was sinnvoll gemacht werden muß, ohne es tatsächlich selbst auszuführen. Dazu kommt, daß man ja beim Erlernen der Befehle, die der logischen Struktur nachgebildet sind, die Struktur selbst lernt - wie bei jeder Sprache.
Und wie bei jeder Sprache muß man auch die Möglichkeit zur Korrektur und Kontrolle haben. Hier helfen zunächst die unter Physikern so beliebten Plausibilitätsbetrachtungen und Abschätzungen als wichtigste Methoden zum Fortschritt im Erkenntnisprozeß. Das mächtigste CAS wird wertlos, wenn man ihm bedingungslos glaubt. Also dürfen beim Unterricht mit CAS die konventionellen Fertigkeiten nicht völlig vernachlässigt werden. Aber auch sie können wieder im Wechselspiel mit dem CAS erarbeitet und gefestigt werden, denn das CAS (die zweite Autorität) läßt sich sehr gut auch als simpler Rechentrainer einsetzen, mit dem man die eigenen Rechnungen überprüfen kann. Besonders wichtig dabei ist, daß nun der Schüler die Lernkontrolle jederzeit selbst durchführen kann. Die Frage nach dem Lösungsheft gehört der Vergangenheit an, wir besprechen reine Rechenaufgaben nur noch in Ausnahmefällen und dann eher so, daß der Schüler eine Anleitung bekommt, wie er das CAS einsetzen kann, um seine Lösung zu kontrollieren. Die Lösung wird nicht vom Lehrer sondern vom CAS bekannt gegeben - Hilfe zur Selbsthilfe, das ist die Methode.
5.3 Leistungsmessung
Natürlich kann nur die Leistung gemessen werden, zu der der Schüler durch den Unterricht befähigt wurde. Wie nun mehrfach dargelegt, entspricht aber ein konsequenter Unterricht mit einem CAS weder inhaltlich noch methodisch noch vom Arbeitsablauf her den im Lehrplan festgeschriebenen Zielen. Es ist vielmehr erklärtes Ziel des Projekts, die für einen neuen Lehrplan notwendige Vorarbeit zu leisten. Nun geht aber der bestehende Lehrplan von der traditionellen Leistungsmessung aus (oder hat sie zum Ziel), die in den Abituraufgaben praktiziert wird: Eingeübte Fertigkeiten werden in einem oft eng abgesteckten Raster in beschränkter Zeit in Klausur reproduziert. Gleichzeitig beklagt man sich über die mangelnde Problemlösefähigkeit und Transferfähigkeit unserer Schüler, beschränkt sich aber trotzdem mit Transferaufgaben auf d)-Teile, damit auch der schwache Schüler noch im a)- und b)-Teil Punkte holen kann. Wir kennen alle diese Diskussion, und viele von uns vermuten, daß hier eine Alibi-Diskussion geführt wird: Es ist einfach für den Korrektor bequem, eine Klausur einem Standardraster entlang korrigieren zu können und außerdem erzeugt ein zentrales Abitur auch noch den Eindruck einer erhöhten Objektivität. Die Objektivität mag sogar gegeben sein, aber mit ihr wird gerade das erstickt, was man nun zu Recht fordert: Weg von der Fertigkeit und dem Drill - hin zum Denken. Ich habe diesen Widerspruch von Anspruch und Praxis in einem der Kurzberichte so formuliert: ‘Die Maple-Klausur ist ein Widerspruch in sich’. Es handelt sich dabei um das zentrale Problem des Projekts, weil es das Problem der Innovation des Mathematikunterrichts schlechthin ist: Man fordert Schlüsselqualifikationen, aber wenn es zum Schwur (Abitur) kommt, werden nur Sekundärtugenden abgecheckt. Das hat mit Bildung wenig zu tun und ist - näher betrachtet - nur eine Pseudo-Objektivität, denn Objektivität kann auch durch die Vergabe von Zehntel-Punkten nicht herbeigezaubert werden. Es ist aber kein sachliches Problem, es ist ein soziales, ein psychologisches. Die öffentlichen Bildungsinstitutionen (-fabriken?) sind weltweit nicht in der Lage, auf individuelle Leistungen einzugehen. Aus Zeit- und Geldmangel trifft man sich deshalb bei einem vertretbaren kleinsten Nenner, einer Meßlatte für die Reproduktionsfähigkeit. Unsere Schüler und Studenten haben das längst gemerkt und sind zu den in den Zeugniskonventen viel gescholtenen Saisonarbeitern geworden oder ‘Scheinstudenten’, die sich kurz vor der Klausur etwas anpauken, um den Schein zu bekommen. Boshafte Zungen behaupten, daß man es so auch zum Scheinarzt, zum Scheinjuristen und Scheinpolitiker bringen kann. In dieser Bildungsmisere steckt auch unser Pilotprojekt (und ist somit eigentlich ein Politprojekt). Diese fatale Fehlentwicklung macht auch uns zu schaffen - gerade uns, denn jegliche Leistungsmessung, die wir durchführen, wird auch als Gradmesser für den Erfolg des Millionenprojekts gewertet werden: Was haben die Schüler nun gelernt (im Fach Mathematik und allgemein)? So wird man fragen. Die Frage ist berechtigt und muß beantwortet werden. Aber nach welchen Kriterien?
Wir können unsere Projektschüler nicht eine Klausur im alten Stil schreiben lassen - sonst hätten wir sie im alten Stil unterrichten müssen und hätten uns damit das Projekt (und eine Million) sparen können. Wir können aber auch nicht von heute auf morgen die Methoden des Unterrichts und der Beurteilung völlig umkrempeln und auf Klausuren ganz verzichten, bzw. wie im Seminarkurs Klausuren durch ‘Seminararbeiten’ ersetzen. Aber es bietet sich ein Kompromiß an:
Die bewährten und auch im CAS-Zeitalter notwendigen Fertigkeiten werden wie bisher schriftlich geprüft.
Die neu zu erwerbenden Fertigkeiten werden (auch in Klausur) am Computer geprüft.
Die eigentliche Fähigkeit ‘Mathematik mit CAS’ wird in Form von Referaten nachgewiesen.
Am Isolde-Kurz-Gymnasium wurden diese Kriterien in Klasse 11 zur Leistungsmessung herangezogen (siehe Bericht...) und zwar mit den Gewichten 1:1:2 (Punkte 1 bis 3). Im Leistungskurs werden sie weiterhin im laufenden Schuljahr verwendet. Leider scheint es im Rahmen des Projekts nicht möglich zu sein, diese Art der Leistungsmessung auch am Abitur beizubehalten, denn die Abiturprüfung soll nur aus Klausuren bestehen.
Ein weiteres Problem ist die Frage der Vergleichbarkeit. Inwiefern haben nun ‘Laptopschüler’ eine andere und vielleicht sogar ‘bessere Mathematik’ gelernt? Ein direkter Vergleich läßt sich nur über schriftliche Arbeiten herstellen, etwa durch eine Arbeit, die parallel in einem konventionellen Kurs geschrieben wird. Schriftliche Arbeiten spiegeln aber nur den geringsten Teil des CAS-Unterrichts wider, und umgekehrt kann der Parallelkurs, ein CAS nicht einmal bedienen, geschweige denn Mathematik damit betreiben. Trotzdem sollte man diesen Test einmal wagen, z.B. in Form einer schriftlichen Arbeit, in der nicht nur Fertigkeiten abgefragt werden, sondern auch Verständnisfragen vorkommen (‘Erläutere den Begriff des Differentialquotienten, ... des bestimmten Integrals,... der Konvergenz...’ wie beim mündlichen Abitur). Im Moment kann ich nur Daten meiner persönlichen Erfahrung (z.B. Fachvorsitz beim mündlichen Abitur) vergleichen. Die oben genannten Fragen können in aller Regel von den Prüflingen nicht beantwortet werden, obwohl es doch um elementare Dinge der Analysis geht. Bei unseren Projektschülern beobachte ich hier mehr Verständnis für Grundsätzliches. Das muß aber nicht CAS-spezifisch sein, wir haben uns eben mehr Zeit dafür genommen, weil wir keine Ableitungsregeln und Kurvendiskussionen pauken mußten.
Schließlich kommt noch eine für bisherige Prüfungen (Klausuren) völlig untypische Situation hinzu: Der ‘Laptopschüler’ hat bei einer ‘Klausur’ mit dem Rechner alle Informationen zur Verfügung, die er jemals auf seiner Festplatte abgespeichert hat. In der Zeitung liest sich das dann so: ‘Der Spickzettel ist erlaubt!’ Diese Formulierung ist typisch. Prüfung heißt bis heute noch immer, daß Fakten und Fertigkeiten vor der Prüfung im Kopf abgespeichert werden und während der Prüfung wiedergegeben werden. Die Fähigkeit, ein Problem mit allen zur Verfügung stehenden Hilfsmitteln zu lösen wird in die Nähe des Täuschungsversuchs gerückt, anstatt sie zu fördern. Dabei sind es gerade diese Fähigkeiten, die der Schüler im späteren Leben brauchen wird: Das Problem einordnen können, wissen welche Hilfsmittel sich zur Lösung eignen, diese Hilfsmittel sachgerecht einsetzen können, das Problem damit lösen und in verständlicher Form dokumentieren. Ich kann die Journalisten beruhigen: Ein Schüler, der diese Fähigkeiten nicht besitzt, fängt mit keiner noch so großen Festplatte etwas an. Mit einem Spickzettel, von dem er die in herkömmlichen Arbeiten oft gefragten Fakten abschreibt, schon.
5.3.1 Klassenarbeit
An dieser Stelle sollen nur die wesentlichen Aspekte hervorgehoben werden. Eine detaillierte Auswertung einer Klassenarbeit steht im Bericht... (siehe...).
Die Standard-CAS-Klassenarbeit (die sich inzwischen auch an den anderen Pilotschulen eingebürgert hat) ist zweistündig und zweiteilig. In der ersten Stunde werden Aufgaben schriftlich und ohne die Verwendung des CAS bearbeitet. In der zweiten Stunde wird das CAS eingesetzt. Es gibt aber auch Variationsmöglichkeiten, wie zum Beispiel eine dreistündige oder gar vierstündige CAS-Arbeit, die demnächst noch getestet werden (das ‘Hauptproblem’ bei diesen Arbeiten wird der Akku sein, der meistens nur für eine Stunde reicht, d.h., es muß für eine ausreichende Anzahl von Netzanschlüssen gesorgt sein). Außerdem wäre auch noch eine CAS-Klausur im Computerraum möglich (zwei mal 10 Schüler), bei der keine selbst gespeicherten Worksheets oder sonstigen Informationen zur Verfügung stehen - quasi als ‘Sprachtest’ wie in einer Informatikarbeit.
Der schriftliche Teil der Arbeiten ist meist so gehalten, daß ein Vergleich mit konventionellen Klausuren möglich ist (aus oben genannten Gründen), also ‘Kurvendiskussion’, geometrische Zusatzfragen, aber (zukünftig vermehrt) auch Verständnisfragen. Diese Teil-Arbeiten haben gezeigt, daß wir es nach wie vor mit ganz ‘normalen Schülern’ zu tun haben. In Punkto Fertigkeiten werden die gleichen Fehler gemacht wie von Schülern, die nicht mit CAS unterrichtet wurden (z.B. Quotientenregel). Diese Fehler treten aber auch nicht häufiger auf. Insgesamt entsteht aber der Eindruck, daß die Schüler souveräner und mit mehr Überblick an Aufgabenstellungen herangehen, und ich vermute, daß das schon auf den Unterricht mit CAS zurückzuführen ist. Um beim Thema ‘Kurvendiskussion’ (als Stellvertreter für die Standardaufgabe) zu bleiben: Auch die am Computer ‘durch Drücken der Return-Taste’ durchgeführte Diskussion (bei der das System und nicht der Schüler selbst rechnet) schult den Blick für das Wesentliche. Mit dem Ergebnis, daß nun Schüler ihre Fehler während der (schriftlichen) Arbeit selbst erkennen und etwa schreiben: ‘Ich muß mich bei der Ableitung verrechnet haben, denn die Kurve kann aus dem und dem Grund höchstens zwei Extrema besitzen...’.
Beim CAS-Teil der Arbeit verwenden wir in letzter Zeit auch explizit Worksheets, die alle Schüler schon auf ihrem Rechner haben (z.B. aus unserem elektronischen Buch) in Transferaufgaben. Etwa: ‘Verwende geeignete Befehle aus dem Worksheet xyz.mws und ändere sie so ab, daß damit gezeigt werden kann...’. Grundsätzlich gilt für CAS-Arbeiten, daß alles verwendet werden kann, was auf dem Rechner steht (s.o.), aber daß auch nach allem gefragt werden kann, was verbindlich auf allen Rechnern stehen muß - und zwar ohne Ankündigung. Letzteres natürlich nur in ‘d)-Teilen’ und behutsam. Die Schüler wissen, daß wir gemeinsam untersuchen wollen, inwieweit der CAS-Unterricht den Transfer fördert, und es sind durchaus schon positive Ansätze zu sehen. Aber man darf - ein weiteres Mal - keine Wunder erwarten, gerade in der Klausursituation (also unter Zeitdruck) kann die zündende Idee nicht erzwungen werden, und es kam schon mehr als einmal vor, daß einem Schüler fünf Minuten, nachdem er die Diskette abgegeben hat, das berühmte Licht aufging. Dann ist es wichtig, daß er seine Arbeit gut dokumentiert hat, damit man bei der Korrektur (interaktiv) im Worksheet nachvollziehen kann, wie nahe er der Lösung war, und somit die bekannte K.O.-Aufgabe vermieden wird.
Es gibt bei CAS-Aufgaben noch einen weiteren Grund für ein K.O.: Das System selbst. Was in herkömmlichen Arbeiten der kleine Rechenfehler mit fatalen Folgen war, ist nun der simple Tippfehler, der eine komplett andere Aufgabe erzeugen kann, auch (und oft gerade) wenn der Schüler mitdenkt. Hier müssen die oben erwähnten ‘Überlebensstrategien’ greifen und der Schüler muß gelernt haben so mitzudenken, daß er mit dem mächtigen System nicht Ergebnisse erzeugt, die mächtig daneben liegen. Leider ist das nicht immer der Fall, und es werden auch Automatismen an unpassender Stelle ungeprüft (und offensichtlich unverstanden) übernommen. Das CAS ist also kein Garant für gelungenen Transfer, aber das hat wohl auch niemand erwartet.
In der Praxis stellt sich dann doch ein Problem des ‘Spickzettels’ heraus. Es war zwar immer beabsichtigt, daß derjenige, der viel mit dem CAS arbeitet, davon auch während der Arbeit Vorteile hat, weil er viele Informationen angehäuft hat und sich darin zurechtfindet, aber es kann natürlich nicht ausgeschlossen werden, daß diese ‘Spickzettel’ kursieren - und auch das ist ja in unserem vernetzten Projekt noch erwünscht. Wo liegt also das Problem? Im sozialen Bereich: Es gibt immer wieder ‘Windschattenfahrer’, die versuchen von einer solchen Situation zu profitieren (was sich aber bei der Korrektur leicht zurückverfolgen läßt, denn jeder Schüler hat seinen eigenen Maple-Dialekt und auch dem Lehrer sind die eigentlichen Autoren aus dem LAN bekannt). In einer Klasse mit einem weniger intakten sozialen Gefüge könnte das zur Cliquenbildung oder auch zu bösem Blut führen. Hier hat es sich bewährt, daß das Los auf eine relativ homogene Klasse fiel (bei der Vergabe des Projekts wurde tatsächlich unter zwei Klassen gelost). Andererseits kann man diesem ‘Problem’ wie immer auch eine positive Seite abgewinnen. Wenn es hier zu Spannungen kommt (die durch die Möglichkeiten der neuen Technologien ausgelöst werden), so hat der Lehrer seine pädagogische Aufgabe wahrzunehmen und die Gruppe ist gefordert, ‘Sozialkompetenz’ zu entwickeln - wie in jedem anderen Unterricht und in jeder anderen Klasse auch.
5.3.2 Referate
Wir kommen zum schwierigsten Teil der Leistungsmessung. Es gibt noch kaum Erfahrungen in der Beurteilung von Mathematik-Referaten, weil es noch kaum Mathematik-Referate gibt. Hier kann ich nur auf meine Praxis der CAS-Kurse der letzten Jahre, aber auch auf etwas Philosophie-Unterricht (und die Erfahrungen aus meinen persönlichen wissenschaftlichen Arbeiten) zurückgreifen, also eher auf Standard-Kriterien aus dem Deutsch-Unterricht, die aber in diesem Fall noch durch die speziellen Anforderungen des Fachs zu ergänzen sind. Hier liegt also eine wesentliche Aufgabe für die Didaktik der neuen Mathematik.
Bei der Beurteilung eines Referats muß man in unserem Projekt immer im Hinterkopf behalten, daß prinzipiell alle Mittel zur Verfügung stehen, vom Schulbuch und Heftaufschrieb bis zum Worksheet, das ein Australier im WWW zur Verfügung stellt. Das kann man so interpretieren, daß dadurch der Beurteilungsmaßstab strenger gewählt werden muß, man kann es aber auch so auslegen, daß es - zumindest in der Anfangsphase - dem Schüler mehr abverlangt, als ein Referat mit eng gestecktem Rahmen. Dazu kommt die Vielfalt der Tätigkeiten, die mit einem CAS möglich werden. Um die Sache einigermaßen in den Griff zu bekommen, haben wir uns auf folgende Bewertungskriterien für den mathematischen Erörterungsaufsatz geeinigt:
Form und Sprache (Deutsch)
Verwendung des CAS (Maple-Sprache, Programmierung)
Mathematik (Schwierigkeitsgrad, Korrektheit)
Originalität (als Bonus)
Eine weitere Aufschlüsselung (insbesondere von Punkt 2 und 3) und die Gewichtung ist nicht zwingend und allgemeingültig festgelegt, weil die Themen sehr unterschiedlich gestellt und bearbeitet werden können, in der Regel haben aber die Punkte 2 und 3 das stärkste Gewicht. So kann es durchaus vorkommen, daß ein Referat, in dem ein einfacher mathematischer Sachverhalt verständlich dargelegt wird, als ebenso gut bewertet wird, wie ein Referat, in dem ein ‘Programmierer’ eine Breitseite von Maple-Befehlen abfeuert, mit der er zwar seine speziellen Maple-Kenntnisse dokumentiert, aber sonst nichts.
Die Bewertung wird grundsätzlich mit den Autoren individuell durchgesprochen, auch vergleichend mit anderen Arbeiten (die ja jeder kennt). Diese Gespräche sind selbst auch Teil der Notenfindung (als Mini-Kolloquium). Wird ein Thema von einer Gruppe bearbeitet (maximal drei Autoren sind zugelassen, je Umfang des Themas), so müssen entweder verschiedene Aspekte von den einzelnen Autoren herausgearbeitet werden, oder die Gruppe teilt sich das Thema so auf, daß eine individuelle Benotung möglich ist.
Zu Beginn von Klasse 11 war dieses Verfahren mit 27 Schülern recht mühsam. Aber im Laufe eines Schuljahres lernt man sich kennen und kann gezielt vorgehen, auch was die zeitliche Planung betrifft: Auch motivierte Projekt-Schüler neigen zum Aufschieben ihrer Arbeit (und haben ‘nebenher’ noch den normalen geschlossenen Unterricht). Deshalb wird nun im Leistungskurs mehr auf die Einhaltung von Abgabeterminen geachtet und die etwas ‘langsameren Schüler’ bekommen ihr Thema als erste (typischer Bearbeitungszeitraum ist sechs Wochen). So ist einigermaßen gewährleistet, daß erstens alle ihr Referat noch vor den Zeugniskonventen abgeben und zweitens nicht durch ständiges Nachbessern die Note unverhältnismäßig hochgeschraubt wird.
Insgesamt gesehen sind wir hier aber noch im Experimentierstadium und das wird wohl auch (wie in den Seminarkursen) noch eine Weile so bleiben, doch die Arbeit lohnt sich!
5.3.3 Korrekturen
In diesem Abschnitt möchte ich mehr auf die Praxis oder Technik der Korrekturen eingehen, die ein computergestützter Unterricht mit sich bringt.
Alle CAS-Produkte der Schüler werden nicht in gedruckter Form weiterverarbeitet, sondern als Dateien. Das hat zwei Gründe (nämlich die beiden Schwerpunkte des Projekts, insbesondere an unserer Schule):
1. Die Arbeit mit einem CAS basiert auf Interaktion (am Computer).
2. Die Arbeit im Netz basiert auf Dateitransfer (von Computer zu Computer).
Zu 1.: Würden die Schüler ihre CAS-Arbeit in gedruckter Form abgeben, so könnte nur das Endergebnis bewertet werden und der Korrektor müßte z.B. bei Syntaxfehlern einen entsprechenden Kommentar handschriftlich eintragen, den dann der Schüler wieder in seinen Computer eintippt. Das ginge noch. Aber ohne die Datei hat der Korrektor nicht die Möglichkeit, das Worksheet voll zu testen, sei es zur Fehlersuche oder zur Überprüfung der tatsächlichen Funktionsfähigkeit oder Optimierung. Auch wenn man sich gut mit Maple auskennt, ist es zuweilen schwierig, die möglichen Reaktionen von Maple im Kopf durchzuspielen, man müßte also als Korrektor das Worksheet abtippen - und das wollte ich mir nicht antun. Die Korrektur läuft also in unserem Leistungskurs so, daß ich die Arbeiten (Klausur oder Referat) der Schüler auf meinen Home-PC hole (per Diskette oder DFÜ) und dort mit ihnen weiterarbeite, denn es soll ja auch untersucht werden, ob und wie das machbar ist.
Dazu werden die Dateien zunächst in geeignete Verzeichnisse gespeichert, und in einer Excelltabelle werden die notwendigen Einträge gemacht (Namen, maximale Punktezahl,...). Dann wird Worksheet für Worksheet korrigiert, d.h., in das Worksheet (genauer eine Kopie davon) werden die Korrekturvermerke und Punkte eingetragen, und parallel dazu die Punktetabelle aktualisiert. Weil es aber am Computer wesentlich zeitaufwendiger ist, zwei Arbeiten zu vergleichen, wenn man sich etwa nicht sicher ist, ob man nun Schüler A und Schüler B gerecht beurteilt hat, wird oft ein zweiter Durchgang notwendig, denn man kann nicht einfach zwei oder drei Hefte aufschlagen und nebeneinander legen. (Übrigens fehlt auch den Schülern nach der Rückgabe der Arbeit dieser ‘konventionelle direkte Vergleich’: ‘Mein Nachbar hat hier 5 Punkte und ich nur 4’.)
Obwohl das Korrigieren in dieser Form also deutlich zeitaufwendiger ist (etwa die doppelte Zeit), macht es auch Spaß, weil man die Möglichkeit zur Interaktion hat. Außerdem kann der Schüler ebenfalls mit dem korrigierten Worksheet weiterarbeiten und so seine Fehler nachvollziehen, verbessern und daraus lernen. Und natürlich steht die korrigierte Klassenarbeit bei der nächsten Arbeit zur Verfügung: Ich mußte noch nie jemanden dazu auffordern, eine Verbesserung zu machen.
Zu 2.: Auch hier (Praxis der Korrektur im Netz) hat sich wieder ein ‘Problem’ herausgestellt, das man erst so richtig sieht, wenn man es macht: ‘Datenschutz’ (die Anführungszeichen, weil es kein gravierendes Problem ist). Die letzten beiden korrigierten Klausuren habe ich en bloc (das gesamte Verzeichnis) vom Home-PC auf das Schulnetz geschickt und diesen Transfer per E-Mail bekannt gegeben. Das hat bei den schwächeren Schülern etwas Unmut ausgelöst, weil sie befürchteten, daß andere sich ihre Arbeiten anschauen. Wir haben das so gelöst, daß ich das entsprechende Verzeichnis nun erst freigebe, wenn sich alle im Computerraum versammelt haben. Dann holt jeder seine Datei (die Notebooks sind mit vernetzt) und löscht sie auf dem Server. Mit dem zusätzlichen Vorteil, daß dann die Arbeit gleich im Computerraum besprochen wird, wo ich durch die Bildschirmvernetzung die Möglichkeit zur Online-Demonstration habe.
Zur Praxis der Korrektur und Beratung via Computer muß aber hier vor allem eines hervorgehoben werden: Unser Domino-Server (detaillierter Bericht folgt). Dieser professionelle Datenbank-Server erleichtert hier die Arbeit nicht nur ganz erheblich (im Vergleich zur Arbeit in Verzeichnissen), er macht überhaupt erst echtes Telelearning möglich. Die Schüler geben nun dort ihre Referate ab, also an einer zentralen Stelle, die von allen (die die Berechtigung dazu haben) einsehbar ist. So kann eine Autorengruppe zusammenarbeiten und die Beratung durch den Lehrer von zu Hause aus erfolgen, und das ist wichtig, denn oft ist in der Schule nicht genügend Zeit, ein Worksheet mit einem Schüler durchzusprechen.
5.3.4 Abitur
Die weitestgehende Folgerung aus den vorangehenden Abschnitten ist, daß der Mathematikunterricht mit CAS durch seine Vielfältigkeit in den Anforderungen, in der Durchführung und Bewertung ein dezentrales Abitur erfordert. Aus diesem Grund werden auch im Projekt schuleigene Aufgaben gestellt. Es ist zwar vertretbar, auch eine Aufgabe zu stellen, die den ‘kleinsten gemeinsamen Nenner’ darstellt, wirkt sich aber nicht besonders vorteilhaft auf den Forscherdrang der Projektteilnehmer aus, und jeder Geleitzug ist bekanntlich nur so schnell wie das langsamste Schiff. [...]
Außerdem plädiere ich nach wie vor entschieden dafür, daß eine Art Seminararbeit zur Abiturprüfung zählt, also die Abitursnote nicht alleine durch Klausuren festgestellt wird. [...]
Neue Abi-Aufgaben siehe [...]
Man wird noch am Ende des Projekts eine Gesamtbilanz ziehen müssen, die sich auch mit dem wirtschaftlichen Aspekt der neuen Technologien an den Schulen beschäftigt. Ich möchte an dieser Stelle nur mit ein paar Streiflichtern beleuchten, wie sich die Akzente im Leben (nicht nur in der Tätigkeit an der Schule) eines Lehrers verschieben, der sich mit den neuen Technologien etwas weiter einläßt.
Wenn es zur Tätigkeit dieses Lehrers gehört, daß er ein Netzwerk betreut, so muß er wissen, daß ein simpler Stromausfall oder eine defekte Festplatte lawinenartige Folgen auslösen können. Nicht nur Reparaturen, sondern auch Neuinstallationen einzelner Softwarekomponenten oder des ganzen Systems können so am Wochenende oder in den Ferien auf einen zukommen, denn ‘die Kisten müssen ja laufen’. Aber auch wenn man von solchen ‘Unglücksfällen’ verschont bleibt, steigt das Arbeitspensum im Vergleich zu einem ‘normalen Lehrerdasein’ gewaltig. Da sind die vielen Kontakte, die sich ergeben, sei es durch E-Mail oder weil bei einem Amt wieder ein Antrag gestellt werden muß, weil das Geld für die Telefongebühren ausgeht. Berichte müssen geschrieben werden und Informationsveranstaltungen organisiert und durchgeführt werden. Die technischen und didaktischen Probleme verschwinden allmählich völlig neben den rein organisatorischen. Man ist eigentlich nur noch unterwegs, um ‘Quartier zu machen’.
Sicher ist die Pilotphase immer arbeitsintensiver als der Normalzustand. Aber es steht genauso fest, daß der ‘technologisierte Normalzustand’ von morgen arbeitsintensiver sein wird als heute. Die Technologien sparen zwar teilweise Arbeit, aber sie machen (noch) mehr Arbeit, und diese Mehrarbeit wird nur durch eine Personaloffensive zu bewältigen sein. Eine Medienoffensive reicht da nicht aus. Im Rahmen meiner Tätigkeit in der Arbeitsgruppe ‘Multimediales Lehren und Lernen’ (6 Stunden Deputatserlaß) habe ich ein halbes Jahr lang Buch über meine Arbeitszeit geführt. Ich kam auf volle 30 Stunden pro Woche (zusätzlich zum Schuldeputat) und es kamen auch Spitzenwerte von 50 Stunden vor (einfach deshalb, weil man am Computer auch nachts, an den Wochenenden und in den Ferien arbeiten kann). Natürlich bin ich nicht der Einzige, der seine Wochenenden am Computer verbringt, das sieht man, wenn man ins Netz schaut, und man weiß es auch so von den Bekannten aus der Branche. Aber es gibt auch nicht beliebig viele Kollegen, die in einer permanenten Pilotphase leben wollen und können, denn das ist auch eine Kostenfrage:
Da sind die Telekom-Kosten, an der Schule und privat. Die Nachrüstung der Computer, an der Schule und privat, der rechtzeitige Umstieg auf die neueste Software, an der Schule und privat, und vieles mehr. Auch Schüler sind von diesen Ausgaben betroffen, gerade die aktiven und förderungswürdigen finanzieren hier oft die Schule aus eigener Tasche mit.
Es wäre also ziemlich illusorisch, davon auszugehen, daß die neuen Technologien schon in naher Zukunft flächendeckend an den Schulen Einzug halten werden. Dafür sind einfach die personellen Ressourcen nicht vorhanden.
7 Zusammenfassung und Ausblick
Das wohl wichtigste Ergebnis kann man den Schülerbefragungen entnehmen (siehe...): Alle Schüler würden wieder ‘Mathematik mit CAS’ wählen. Ebenso ist die Kurswahl (LK: 21 GK: 6) ein deutliches Indiz dafür, daß der konsequente Einsatz der neuen Technologien nicht nur machbar ist, sondern von den Schülern voll akzeptiert wird.
Gesamtsituation:
Bei einer Bewertung - auch im Hinblick auf die geforderte Übertragbarkeit - sollte man nicht vergessen, daß in einem solchen Projekt die Motivation von Anfang an sehr hoch ist und durch geeignete Gestaltung des Projekts auch für die gesamte Dauer sehr hoch gehalten werden kann. Die neuen Technologien werden auch in anderen Fächern eingesetzt, wodurch sich viele positive ‘Nebeneffekte’ erreichen lassen, wenn Schüler und Lehrer streckenweise eine Verdoppelung der Arbeitszeit in Kauf nehmen. Dies zeigt aber auch, daß bei entsprechender Motivation unsere Schüler durchaus belastbar sind.
Problematisch:
Insbesondere für die Akzeptanz bei flächendeckender Einführung ist die Technikhürde relativ hoch. Der verstärkte Einsatz des Mediums Computer bedeutet eine Doppelbelastung.
Neue Arbeitsformen sind ungewohnt und am Anfang fehlt die Orientierung in der neuen Umgebung. Auch nach der Eingewöhnung neigen manche Schüler dazu, in den konventionell unterrichteten Fächern (also der Mehrzahl), in denen 'Druck gemacht wird', mehr zu arbeiten (insbesondere vor Klausuren in diesen Fächern).
Rechenfertigkeiten treten in den Hintergrund.
Die Prüfungsformen müssen sich nach den Arbeitsformen richten. Inwiefern ist das (flächendeckend) technisch machbar und politisch durchsetzbar (Seminararbeit)? Das Zentralabitur paßt wie gesagt überhaupt nicht zu einem Unterricht, in dem selbständig gearbeitet wird, Probleme in Projekten gelöst werden und auf Vielfalt, Individualität und Kreativität Wert gelegt wird.
Positiv:
Die Beteiligung und Aktivität der Schüler steigt um 100% (Idealzustand?). Referate in den Ferien, Mathematik als Hobby. Arbeits- und Sozialformen fördern selbstverantwortliches und kontinuierliches Lernen. Die von Lehrern gefürchtete Saisonarbeit kommt praktisch nicht vor. Diese positiven Auswirkungen wurden auch von den Kollegen in den anderen Fächern bestätigt.
Schon in Klasse 11 deutlicher Reifungsprozeß, sozial aber auch fachlich: Der kompetente Schüler als
Techniker: Der ständige Umgang mit der Technik wirkt ‘selbsterziehend’.
Forscher: Die Vielzahl an Möglichkeiten bei der Arbeit mit CAS und im Netz ist wesentlich realistischer als Frontalunterricht. Der Schüler lernt, durch Erfolg und Mißerfolg ein Ziel zu erreichen, ohne daß er für den Mißerfolg bestraft wird (wie im Berufsleben).
Lehrer: Der Schüler kann Erlerntes weitergeben und erwirbt so auf natürlichem Weg didaktische und methodische Fähigkeiten.
Autor: Durch die Dokumentation (in Worksheets und im Internet) wird der Schüler zur verständlichen und formal ansprechenden Wiedergabe seiner Erkenntnisse erzogen.
Organisator: Beim Umgang mit der Fülle von Materialien (auf dem eigenen Rechner und im Netz) erlernt der Schüler die zweckmäßige Abfolge von Tätigkeiten und die Abstimmung mit Tätigkeiten anderer.
Team: Hier bildet sich Toleranz und Verantwortungsbewußsein.
Insgesamt wird durch ‘Telelearning’ die Effizienz des Unterrichts wesentlich gesteigert. Unterricht heißt nicht mehr Optimierung einer Schulstunde durch ein ausgefeiltes didaktisches Konzept (etwa: Einstieg, Höhepunkt bei zwei Drittel, Fixierung des Ergebnisses und dann Übungsphase und HA). Nein, Unterricht geht hier rund um die Uhr, so lange der Lehrer es will und kann. Er ist potentiell immer für alle erreichbar und betreut seine Schüler auch von zu Hause aus. Das CAS selbst bewirkt im Mathematikunterricht ebenfalls eine Steigerung der Effizienz, aber nicht in erster Linie in dem Sinne, daß nun alte Inhalte schneller und gründlicher gelernt werden, sondern daß die Schüler sich wesentlich intensiver mit der Materie beschäftigen. Das kann auch mehr Zeit kosten als im herkömmlichen Unterricht. Kurz: Ein CAS ist kein Nürnberger Trichter, mit dem sich das im Lehrplan geforderte Wissen schneller abfüllen läßt.
Ziele:
Die Ziele der herkömmlichen Lehrpläne müssen sicher in Frage gestellt werden (Mathematikabitur als Selbstzweck ohne Bezug zur Realität). Viele davon haben sich aber auch bewährt. Hierzu zählen insbesondere die oft nur in den Präambeln aufgeführten. Zum Beispiel (sinngemäß):
Ausführliche Begründungsphasen
offene Fragestellungen
Deutsch im Mathematikunterricht
Vorbereitung für lebenslängliches Lernen
Umgang mit den neuen Techniken (auch Gymnasiasten kommen ins Berufsleben)
Versuch einer Antwort auf die 'drei zentralen Fragen':
Welche Innovationen kommen auf uns zu?
Als Betatester habe ich aus nächster Nähe miterlebt, weshalb sich die Entwicklung von Software ständig beschleunigt: In größeren Softwarefirmen arbeitet man weltweit vernetzt an der Softwareentwicklung. Was heute noch wie eine Vision aussieht, kann schon morgen Realität sein. Aussagen wie ‘Maple eignet sich nicht zur Behandlung der Unterrichtseinheit xy’ sind also in doppelter Hinsicht falsch: Erstens steht es nicht von vornherein fest, daß es überhaupt sinnvoll ist, die Unterrichtseinheit xy zu behandeln, zweitens kann die ‘Maple-Schwäche’ oft über Nacht kuriert sein. Vielleicht wird man schon in 5 Jahren den PC einfach mit der Lösung von Textaufgaben beauftragen können. Die Innovationen sind umfassend und erreichen alle Ebenen vom einzelnen PC bis ins WWW: Online-Mathematik mit Java-Scripts, Bildungsangebot außerhalb der Schulen und außerhalb der Lehrpläne. Kurz: Alle Innovationen, die wir uns vorstellen können, kommen auf uns zu. Für manche muß man Visionär sein, manche sieht man aber schon jetzt mit bloßem Auge: Durch die Vernetzung werden wir (Lehrer) schon bald gezwungen sein, uns neue Aufgaben und Themen einfallen zu lassen (der Spickzettel ist wirklich erlaubt).
Welche Innovationen sind für den Unterricht von Relevanz?
Wir können uns nicht auf den Standpunkt stellen, daß die ehrwürdige alte (Schul-) Mathematik eine feste Größe ist. Schon gar nicht läßt sich von diesem Standpunkt ableiten, daß Innovationen in diese Mathematik eingearbeitet werden. Vielmehr handelt es sich heute mehr denn je um eine Wechselwirkung der Technologien mit den Inhalten und Methoden der Mathematik. Man kann genau so gut fragen, was vom Mathematikunterricht relevant für die Computerwelt ist (ich fürchte nicht viel!). Umgekehrt steht aber fest, daß die neuen Technologien mit fast all ihren Möglichkeiten (Textverarbeitung, Computeralgebra, Multimedia, Datenbanken, Internet) jeglichen Unterricht stark beeinflußen werden: Der Computer wird zum Hauptmedium. Allerdings ist die Entwicklung, wie dieses Medium in den Unterricht übernommen wird, schlecht planbar. Es ist eher ein natürlicher Prozeß, der auch von der Akzeptanz reguliert werden wird. Dabei sind wohl gesellschaftliche Fragen und Auswirkungen wichtiger als fachdidaktische Details. Das bedeutet, daß die Fragen nach der Relevanz, die mir immer wieder in erster Linie von Leuten gestellt werden, die ein CAS noch nie aus der Nähe gesehen haben ('Und was bringt das nun?' 'Wozu ist das im laufenden Unterricht gut?' 'Was ist der entscheidende Unterschied mit und ohne CAS?'), keine hohe Relevanz haben. Was im Moment alleine zählt, ist die Bereitschaft, sich mit den Innovationen vertraut zu machen. Erst dann kann man die Sinnfrage zu stellen.
Umsetzung in die Praxis?
Die einzelnen Schritte sind nicht einfach zu planen. Aber eines ist klar: Es handelt sich in erster Linie um eine Personalfrage! Damit ist nicht nur die Finanzierung von Stundennachlässen (z.B. Netzwerkbetreuung) gemeint oder eine massive Fortbildung (ebenfalls mit Stundenanrechnung), sondern auch das 'mittlere Management'. Auf diversen Multimedia-Kongressen wurde das von Vertretern aus der Wirtschaft und auch von Vertretern aus der Kultusverwaltung immer wieder betont: In 'Betrieben' ab einer gewissen Größenordnung (z.B. die Gesamtheit der Schulen Baden-Württembergs als ein 'Betrieb' des Landes) liegt das hauptsächliche Hemmnis für Innovationen in der Verwaltung. Die Innovation von unten findet von selbst statt und die Innovation von oben läßt sich leicht vordenken und propagieren. Aber die Innovation 'aus der Mitte' ist immer problematisch, weil hier der geringste Handlungsbedarf besteht (subjektiv). Wir sind hier aber ein gutes Stück weitergekommen. Um die positive Entwicklung zu verstärken, sollte speziell bei der Modernisierung des Mathematikunterrichts beachtet werden:
- Computer-Algebra-Systeme müssen frühzeitig im Unterricht eingesetzt werden, etwa in der Informationstechnischen Grundbildung (ITG) in Klasse 8 als erste Programmiersprache. Nur so werden sie für Schüler (und Lehrer) in der Oberstufe zur Selbstverständlichkeit.
- Die Prüfungen müssen an den Unterricht mit CAS angepaßt werden. Das Diktat des Zentralabiturs (das Pauken von Abi-Aufgaben, die den tatsächlichen Lehrplan darstellen) muß entfernt werden. Dieses Diktat ist eines der schwerwiegendsten formalen Hemmnisse für jede Innovation.
- Das Vertrauen in die Lehrerschaft muß wieder hergestellt werden. Was hat das mit Neuen Technologien und der Umsetzung von Innovationen zu tun? Sehr viel! Die meisten Lehrer haben bis jetzt wohl pflichtbewußt und mit Engagement das unterrichtet, was im Lehrplan stand. Trotzdem bescheinigt die 'berühmte TIMS-Studie' deutschen Schülern allenfalls Mittelmaß. Es hätte verheerende Folgen, wenn man die Lehrer dafür verantwortlich machen würde, denn trotz ihres hohen Durchschnittsalters und des täglich wachsenden Aufgabenpensums haben viele immer noch genügend Potential zur Innovation, sofern man ihnen genügend Spielraum läßt.
Ich bedanke mich im Sinne des letzten Punktes für das uns entgegengebrachte Vertrauen und den großen Spielraum, den wir in diesem Projekt haben.
Mein besonderer Dank gilt aber den Mitwirkenden, insbesondere den Schülern des Mobilen Klassenzimmers. Woran werden sie sich in 30 Jahren erinnern?
Die gekürzte Fassung des Abschlußberichts (mit Abitur) gibt es hier.
HOME | Projekte | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top