Funktionen einer Variablen

Polynome

In der Regel wird man sich die Funktion zuerst zeichnen.

> restart:

> f:=x^4-x^2;

> plot(f,x);

Nur weiß man den günstigen Bereich nicht immer von vornherein. Also kann man es mit dem Befehl extrema versuchen.

> extrema(f,{},x,'s');s;

Dieser Befehl ist eigentlich für die Bestimmung von Extrema multivariabler Funktionen (mit Nebendedingungen) gedacht (s.u.), kann aber auch hier bedingt eingesetzt werden. Dazu ordnet man zunächst die möglichen Extremstellen (sort(..,`<`) funktioniert nur für type numeric, wozu Wurzeln nicht gehören):

> kand:=sort([seq(eval(x,gl),gl=s)],(x,y)->is(x<y));

Oder etwas umständlicher:

> #x1:=min(seq(evalf(op(s[i,1])[2]),i=1..nops(s)));

> #x2:=max(seq(evalf(op(s[i,1])[2]),i=1..nops(s)));

Nun können wir eine Zeichnung mit angepaßtem Plotbereich erstellen.

> plot(f,x=kand[1]-1..kand[-1]+1);

>

Der Befehl extrema liefert nur die Kandidaten für Extrema, untersucht also nur die notwendige Bedingung:

> f:=x^3;

> extrema(f,{},x,'s');s;

Und wenn kein Extremum existiert, liefert extrema ein komplexes Ergebnis:

> f:=x^3+x+1;

> extrema(f,{},x,'s');s;

>

Trotzdem kann man auf diese Art bequem eine 'Minikurvendiskussion' schreiben.

> restart:

> kd:=proc(f)
global stellen:
extrema(f,{},x,'s');
stellen:=sort([seq(evalf(Re(op(s[i,1])[2])),i=1..nops(s))]);
print(seq([stellen[i],subs(x=stellen[i],f)],i=1..nops(s)));
plot(f,x=stellen[1]-1..stellen[-1]+1);
end;

>

> kd(x^4-3*x^2+x);

>

Aber wie gesagt - man muß mitdenken:

> kd(x^3+x+2);

>

Wenn wirklich Extrema vorliegen

> f:=x^4/2-4*x^2;

> kd(f);

kann man sie auch mit minimize und maximize finden.

> minimize(f,x,location);

> maximize(f,x=-1..1,location);

> maximize(f,x,location);

>

> f:=int((x+2)*x*(x-1),x)+1;

> kd(f);

> minimize(f,location);

>

Aber hier streikt minimize:

> g:=x^4-3*x^2+x;

> kd(g);

> minimize(g,x,location);

Das liegt daran, daß Maple bei der Lösung von kubischen Gleichungen und Gleichungen vierten Grades 'durch das Komplexe geht' (wenn es erforderlich ist):

> solve(diff(g,x));

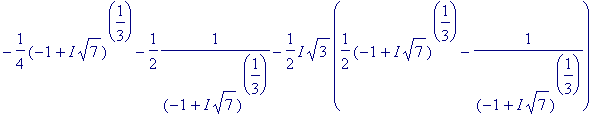
> evalc([%]);

>

Dann rechnet minimize nicht weiter. Das kann aber so umgangen werden:

> _EnvExplicit:=false;

> minimize(g,x,location);

> evalf(%);

>

Für Polynome vom Grad > 5 (also Grad der Ableitung > 4) ist dies nicht erforderlich, weil dann immer die RootOf-Darstellung genommen werden muß.

> _EnvExplicit:=true;

> h:=convert(series(sin(x),x,8),polynom);

> kd(h);

> evalf(minimize(h,x=-4..0,location));

Minimize gibt übrigens das absolute Minimum zurück (dgl. für maximize):

> evalf(minimize(h,x=-4..4,location));

>

Gebrochenrationalen Funktionen

Bei gebrochenrationalen Funktionen lässt sich minimize auch so einsetzten:

> f:=(x^4+x+7)/(x^6-4);

>

> plot(f,x=-5..5,-10..10);

Bestimmung der Pole

> minimize(f,location);

> -1.259921050^3;

> evalf(%);

> evalf(maximize(f,x,location));

Relatives Maximum:

> maximize(f,x=-1..1,location);

> evalf(%);

Und die Asymptote

> minimize(f,x=2..infinity,location);

>

Trigonometrische Funktionen

> minimize(sin(x),location);

> minimize(tan(x),location);

Exponential- und Logarithmusfunktionen

> minimize(exp(x),location);

> minimize(exp(-(x+4)^2),location);

> maximize(exp(-(x+4)^2),location);

> minimize(ln(x),x,location);

> minimize(1/ln(x),x=1..infinity,location);

> maximize(1/ln(x),x=1..infinity,location);

Hier gibt es Probleme

> minimize(1/ln(x),x,location);

Error, (in kernels) too many levels of recursion

> minimize(ln(x)^2);

Error, (in minimize/cell/power/univariate) complex argument to max/min

> assume(x>1):minimize(ln(x)^2);

Error, (in minimize/cell/power/univariate) complex argument to max/min

Aber

> x:='x':minimize(ln(x)^2,x=0..infinity,location);

>

>

Transzendente Funktionen (allgemeiner Fall)

> minimize(sin(x)+x,x=1..4,location);

> minimize(sin(x)+2*x,x=0..4,location);

> minimize(sin(x)+2*x,x,location);

Übrigens:

> extrema(sin(x)+2*x,{},x,'s');s;

> x:='x':

> diff(sin(x)+2*x,x);

> solve(%);

> evalf(arccos(2));

> cos(%);

> minimize(x*sin(x),x);

Aber

> minimize(x*sin(x),x=1..12);

> minimize(x*sin(x),x=1..10);

> diff(x*sin(x),x);

> solve(%);

> allvalues(%);

>

> minimize(exp(x)+x);

> minimize(exp(x)*x,location);

> maximize(x*exp(-(x-1)^2),location);

>

Noch ein Beispiel

> f:=x^2+sin(x)+cos(2*x);

> minimize(f,x);

Das Minimum kann nicht gefunden werden, weil die transzendente Gleichung nicht gelöst werden kann

> solve(diff(f,x));

> _SolutionsMayBeLost;

> _SolutionsMayBeLost:='_SolutionsMayBeLost':

> fsolve(diff(f,x));

> _SolutionsMayBeLost;

>

Funktionen von mehreren Variablen (Untersuchung mit minimize und maximize)

> minimize(x*y,location);

> minimize(x*y,x=1..10,y=1..10,location);

> minimize(x^4-x^2+y^4-y^2,location);

> #plot3d(x^4+y^4-x^2-y^2,x=-2..2,y=-2..2);

>

> minimize(sin(x)*cos(y),location);

> minimize(sin(x)*cos(y),x=0..50,y=0..4,location);

>

Hier gibt es wieder Probleme

> minimize(sin(x*y),x=0..3,y=0..3,location);

Error, (in minimize/cell/addpoint) wrong number (or type) of parameters in function union

> minimize(sin(x*y),x);

Error, (in unknown) too many levels of recursion

Achtung: das erzeugt einen Endlosausdruck, aber kein Ergebnis! (Mit Stop abbrechen und printlevel wieder auf 1 setzen)

> printlevel:=200:

> minimize(sin(x*y));

Warning, computation interrupted

> printlevel:=1:

>

Extrema von Funktionen mehrer Veränderlicher mit Nebenbedingungen

> restart:with(plots):

Warning, the name changecoords has been redefined

Üblicher Lösungsweg bei zwei Variablen und einer Nebenbedingung

> Z:=x*y; N:=x^2/3-y=25;

> #Z:=x^2*y/10; N:=x^2/3-y=25;

> yx:=solve(N,y);

> zx:=subs(y=yx,Z);

> simplify(diff(zx,x));

> solve(diff(zx,x));

>

Lösung mit dem Befehl extrema

> extr:=extrema(Z,{N},{x,y},'L');L;

> #allvalues(L); # für RootOfs

Veranschaulichung der Zielfunktion

> zf:=plot3d(Z,x=-10..10,y=-30..20,color=grey):zf;

Die Nebenbedingung als Fläche

> nbimpl:=implicitplot3d( N ,x=-10..10,y=-30..20,
zz=-200..200,style=patchnogrid,color=yellow,grid=[20,20,5]):#nbimpl;

> display(zf,nbimpl);

Die Nebenbedingung als Raumkurve

> nb:=spacecurve([x,yx,zx],x=-10..10,color=black, thickness=2,axes=normal):display(nb,orientation=[-40,60]);

Zwei Projektionen

> display(nb,orientation=[0,90]);

> display(nb,orientation=[-90,90]);

Vgl. üblicher Lösungsweg

> plot(zx,x=-10..10);

>

> #display(zf,nb);

> display([zf,nb,nbimpl],axes=boxed);

>

Lösungspunkte

> punkt1:=pointplot3d([subs(op(L[1]),x),subs(op(L[1]),y),subs(op(L[1]),Z)],symbol=cross,symbolsize=50,color=red):

> punkt2:=pointplot3d([subs(op(L[2]),x),subs(op(L[2]),y),subs(op(L[2]),Z)],symbol=cross,symbolsize=50,color=red):

> #display(punkt2,punkt1,axes=boxed);

> display([zf,nb,nbimpl,punkt1,punkt2],axes=boxed);

>

Veranschaulichung der Methode der Lagrangemultiplikatoren

> Z,N;

> Nl:=lhs(N)-25;

> sys:={Nl,diff(Z+lambda*Nl,x),diff(Z+lambda*Nl,y)};

>

> solve(sys);

> la:=plot3d(Z+5*Nl,x=-10..10,y=-30..20,axes=boxed,style=patchcontour,contours=30,color=grey):

> display(la,punkt1,punkt2,nbimpl,nb);

Oder als Animation

> ll:=seq(display([plot3d(Z+lambda*Nl/4,x=-10..10,y=-30..20,axes=boxed,style=patchcontour,contours=30,color=grey),punkt1,punkt2,nb]),lambda=-30..20):

> display(ll,insequence=true);

>

>

Weitere Beispiele

Maximales Volumen eines Quaders zu gegebener Oberfläche A

> Z:=x*y*z;

> N:=2*(x*y+y*z+x*z)-A;

> los:=extrema(Z,{N},{x,y,z},'s');

> s;

> A:=6;

> los;

> s;

Sollte der Einheitswürfel sein :-))

Kontrolle

> A:='A':

> sys:=seq(diff(Z+lambda*N,k),k=[x,y,z]),N;

> sol:=solve({sys},{x,y,z,lambda});

> assign(sol);

> Z;

>

Kürzester Abstand des Punktes (x0|y0|z0) von der Ebene a*x+b*y+c*z+d=0

> restart:

> Z:=(x-x0)^2+(y-y0)^2+(z-z0)^2;

> N:=a*x+b*y+c*z+d;

> lot:=extrema(Z,{N},{x,y,z},'s');

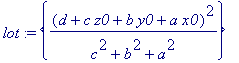
> s;

> a,b,c,d:=3,4,5,6;

> x0,y0,z0:=1,2,3;

> sqrt(op(lot));

> s;

>

Extremale Abstände Punkt - Kugel

> restart:

> Z:=(x-x0)^2+(y-y0)^2+(z-z0)^2;

> N:=(x-xk)^2+(y-yk)^2+(z-zk)^2-rq;

> lote:=extrema(Z,{N},{x,y,z},'s');

> s;

>

> xk,yk,zk:=0,0,0;

> rq:=1;

> x0,y0,z0:=0,1,2;

> lote;

> evalf(lote);

> s;

> evalf(s);

> allvalues(sqrt(op(lote)));

> allvalues(s);

>

Extremale Abstände von Schnittkreis Kugel - Ebene zu geg. Punkt

> restart:with(plottools):with(plots):

Warning, the name changecoords has been redefined

Zielfunktion und Nebenbedingungen

> Z:=(x-x0)^2+(y-y0)^2+(z-z0)^2;

> N1:=(x-xk)^2+(y-yk)^2+(z-zk)^2-rq;

> N2:=a*x+b*y+c*z+d;

Allgemeine Formel

> lote:=extrema(Z,{N1,N2},{x,y,z},'s'): # man kann sich das auch ausgeben lassen...

Daten

> xk,yk,zk:=0,0,0;

> rq:=9;

> x0,y0,z0:=0,1,5;

x0,y0,z0:=-1,1,-2;

> a,b,c,d:=1/2,-1,1,-1/2;

> lote;

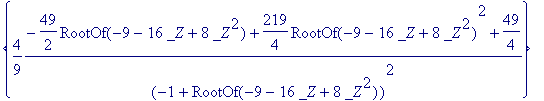
> s;

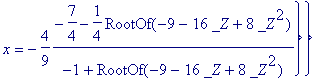
> allvalues(op(s));

Punkte

> sf:=evalf(allvalues(op(s)));

> p1k:=eval([x,y,z],sf[1]);

> p2k:=eval([x,y,z],sf[2]);

Abstände

> map(sqrt,[evalf(allvalues(op(lote)))]);

Zeichnung

> ku:=sphere([xk,yk,zk],sqrt(rq),style=line,color=grey):

> p:=pointplot3d([x0,y0,z0], color=blue,symbol=cross,symbolsize=40):

> p1:=pointplot3d(p1k, color=red,symbol=cross,symbolsize=40):
p2:=pointplot3d(p2k, color=black,symbol=cross,symbolsize=40):
l1 := line([x0,y0,z0], p1k, color=red):
l2 := line([x0,y0,z0], p2k, color=black):
eb:=plot3d(solve(N2,z),x=xk-sqrt(rq)..xk+sqrt(rq),y=yk-sqrt(rq)..yk+sqrt(rq),style=line,color=yellow):

> display(ku,p,p1,p2,l1,l2,eb,scaling=constrained,axes=framed);

>

Optimierungsaufgaben mit zwei Variablen

> restart:

> with(simplex): with(plots):

Warning, the protected names maximize and minimize have been redefined and unprotected

Warning, the names changecoords and display have been redefined

> bed:={2*x1+4*x2<=170, 2*x1+2*x2<=150, 6*x2<=180};

Bei zwei Variablen lassen sich die Bedingungen mit plots[inequal](lineare Ungleichung) graphisch darstellen

> graph:=inequal( bed, x1=0..100,x2=0..80,
optionsfeasible=(color=grey),
optionsclosed=(color=green, thickness=3),
optionsexcluded=(color=yellow),scaling=constrained ):graph;

Zielfunktionen zur Auswahl

> ziel:=300*x1+500*x2;

ziel:=300*x1+300*x2;

ziel:=300*x1+600*x2;

ziel:=300*x1+602*x2;

ziel:=300*x1+150*x2;

> gl:=solve(ziel=q,x2);

> ziele:=plot({seq(gl,q=seq(8*coeff(ziel,x2)*i,i=0..10))},x1=0..100,x2=0..80,color=black,scaling=constrained):#ziele;

> display(ziele,graph);

Es ist diejenige Gerade mit dem größten x2-Achsenabschnitt gesucht, die mit dem zulässigen Bereich mindestens einen gemeinsamen Punkt.

> los:=maximize(ziel, bed );

> opt:=subs(los,ziel);

> optg:=subs(q=opt,gl);

> display([plot(optg,x1=0..100,color=red,thickness=3),ziele,graph]);

>

'Probe'

> subs(los,bed);

>

Sonderfall: Das Optimum wird längs einer Kante angenommen

> restart:

> with(simplex):

Warning, the protected names maximize and minimize have been redefined and unprotected

> bed:={2*x1+4*x2<=170, 2*x1+2*x2<=150, 6*x2<=180};

> ziel:=300*x1+600*x2;

Maple berechnet auch bei der Wahl eines Pivots durch den Benutzer die beiden möglichen Eckpunkte nicht reproduzierbar:

> alias(n=NONNEGATIVE):alias(u=UNRESTRICTED):

> sn:=setup(bed,n);

> infolevel[all]:=1;

> piveq1:=pivoteqn(sn,x1);

> piv1:=pivot(sn,x1,piveq1); Z1:=subs(piv1,ziel);

> piveq2:=pivoteqn(sn,x2);

> piv2:=pivot(setup(bed),x2,piveq2); Z2:=subs(piv2,ziel);

>

> maximize(ziel,setup(bed),n );

> maximize(Z1,bed,u);

> maximize(Z1,piv1);

maximize:   Objective function unbounded

> maximize(ziel,bed,n);

> maximize(Z2,piv2,n );

> #maximize(Z2,piv2,u);

> #maximize(Z2,piv2);

>

> maximize(ziel,bed,n,'sys' );sys;

> #setup(bed);

> maximize(ziel,setup(bed),n );#sys;

> maximize(ziel,bed,u);

> maximize(ziel,bed);

> subs(%,ziel);subs(%%,bed);

> maximize(ziel,bed,n);

> subs(%,ziel);subs(%%,bed);

> #infolevel[all]:=5:

> #maximize(ziel,bed,n);

>

maximize(ziel,bed,NONNEGATIVE,'sys' ); # !! nicht reproduzierbar !!

sys;

maximize(ziel,bed,UNRESTRICTED,'sys' ); # !! nicht reproduzierbar !!

>

>

Optimierungsaufgabe mit mehr als zwei Variablen

> restart: with(simplex):

Warning, the protected names maximize and minimize have been redefined and unprotected

> Z:=53*x1+50*x2+60*x3+90*x4;

> B:={30*x1 + 22*x2 + 18*x4<=600,
10*x1 + 11*x2 + 25*x3 + 9*x4<=800,
16*x1 + 41*x4<=370,
42*x1 + 43*x3 + 37*x4<=500,
15*x1 + 23*x2 + 29*x3 + 21*x4<=700};

>

> L1:=maximize( Z, B, NONNEGATIVE, 'sys' );

> subs(L1,Z);

> subs(L1,B);

> sys;

>

Möglichkeiten zur graphischen Darstellung

Zweidimensional

> Bs:=subs(x1=0,x3=0,B),x2=0..80,x4=0..80;
#Bs:=subs(L1[3],L1[4],B),x1=0..80,x2=0..80;

> plots[inequal](Bs, optionsexcluded=(color=yellow) );

>

Dreidimensional

> Beq:=convert(B,equality);

> Be:=seq(isolate(Beq[i],x1),i=1..5);

> Bep:=map(rhs,subs(x4=0,{Be})),x2=0..80,x3=0..80;

> plot3d(Bep,axes=normal,view=[0..40,0..40,0..40],color=grey,orientation=[-70,65]);

>

>

Transportproblem

> restart: with(simplex):

Warning, the protected names maximize and minimize have been redefined and unprotected

> kies := [220, 290, 320]:

> baustelle := [160, 330, 340]:

> kosten:=array([[10,15,18],[10,17,19],[16,19,20]]);

> x:='x':i:='i':j:='j':

> x := array(1..3,1..3):

> restr := {seq( sum(x[i,'j'],'j'=1..3)=kies[i], i=1..3)} union
{seq( sum(x['i',j],'i'=1..3)=baustelle[j], j=1..3)};

>

> ziel:=add(add(x[i,j]*kosten[i,j],i=1..3),j=1..3);

> minimize(ziel, restr, NONNEGATIVE);

>

> assign(%);

> ziel;

> eval(x);

>

>