PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 5.3.3

Worksheet bohm_10.mws

>

c ITP Bonn 1995                                                                         filename: bohm.ms

Autor: Komma                                                                             Datum: 27.5.95

Thema: Quantenpotential am Doppelspalt mit Feynman-Propagator nach C.Phillipidis et al. Nuov.Cim. vol.52 B, N.1 p.15 Jul.79

Untersuchungen zum Quantenpotential nach C.Phillipidis et al. Nuov.Cim. vol.52 B, N.1 p.15 Jul.79

>

Läuft in Maple 6 wesentlich besser als in V5

>	restart: with(plots):with(linalg):

Konstanten für evtl. Gebrauch bereit stellen (Größenordnung):

>

a:=m/hq;

>	m:=10^(-30):hq:=6.6*10^(-34)/2/Pi;

>

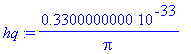
evalf(a);

>

a:='a':

Bezug: C.Phillipidis et al. Nuov.Cim. vol.52 B, N.1 p.15 Jul.97

Gleichungen 7 und 8 S.20, ohne zeitabh. Normierungsfaktor. Feynmans Propagator wird dort mit vereinfachender Annahme verwendet: Wellenpaket hat in x-Richtung die Breite oo, kann ggf. mit xt (s.u.) geändert werden. Ebenso erscheint die Setzung T=X/Vx gewagt: sie liefert einen zeitunabhängigen Propagator, bzw. den Wert des Propagators zu verschiedenen Zeiten (je x), als würde man ihn mit der Teilchengeschwindigkeit Vx durchlaufen und die Momentaufnahmen festhalten und in einem Bild darstellen. Konsequent wäre es, den Propagator als Funktion des Ortes und mit der Zeit als Parameter zu betrachten. Die Koordinatenwahl ist nicht besonders günstig, weil asymmetrisch, das Vorzeichen von Vy ist problematisch (Vy  kann aber in der Regel vernachlässigt werden - parallele Strahlen, senkrechter Einfall).

>	arga1:=I*a/2*(x0^2/t0+x^2/t);

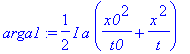
>	arga2:=I*a/2*(y0^2/t0+y^2/t);

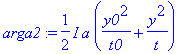
>	arga3:=(a^2/2/t^2*((vy*t-y)^2+xt))/(I*a/t0+I*a/t-1/s^2);

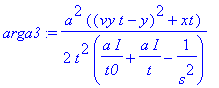
>	argb1:=arga1;

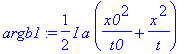
>	argb2:=I*a/2*(y0^2/t0+(2*y0+y)^2/t);

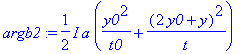
>	argb3:=(a^2/2/t^2*((vyb*t+2*y0+y)^2+xt))/(I*a/t0+I*a/t-1/s^2);

>

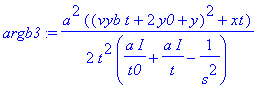
arga1 und argb1 werden für den Betrag nicht benötigt

>	psia:=exp(arga1+arga2+arga3);

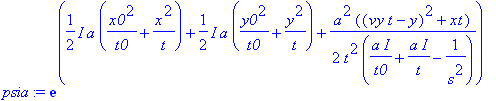
>	#psia:=exp(arga2+arga3);

>	psib:=exp(argb1+argb2+argb3);

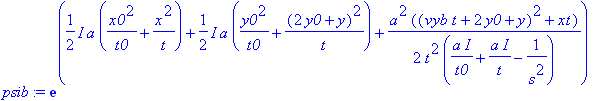
>	#psib:=exp(argb2+argb3);

>	psi:=psia+psib;

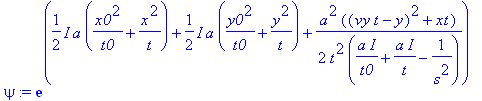
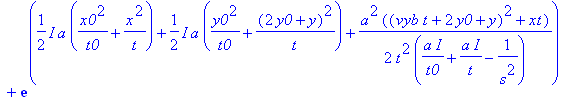
>	#xt:=(vx*t-x)^2;

>

xt:=0:

>	A:=evalc(abs(psi)):

>

#A;

>	qpot:=laplacian(A,[x,y])/A:

>

#qpot;

Symmetrische Koordinaten

>	unassign('x0','y0','a','t0','vx','vy','s','t','x'):

>	qpots:=subs(y=y-y0,qpot):

(Mehrfache unassignments zur Absicherung der Einstiegspunkte)

>	unassign('x0','y0','a','t0','vx','vy','s','t','x'):

>	t0:=x0/vx;

>

t:=x/vx;

>

#qpot;

Bei der Definition von t0 via x0 wird die Darstellung in x-Richtung verschoben.

Das Vorzeichen von vyb ändert einiges, das merkt man aber erst, wenn man den Betrag genügend groß wählt, d.h.den Doppelspalt divergent beleuchtet (oder schief?). Aber es muß wohl in psib doch +vy heißen (das bewirkt u.a. Reflexion ...)

>

Es ist äußerst interessant, wie das Quantenpotential von den verschiedenen *Annahmen* abhängt! Z.B. beeinflußt die Spaltbreite s das Erscheinungsbild sehr stark.

Geeignete Parameter für kleinere Zahlen (als im Jönsson-Exp.), nicht zu stark ändern, man verliert die Erscheinung leicht aus dem Visier:

>	vy:='vy': vyb:=vy:

>	#x0:=0.10:

>

y0:=1:

>	vx:=2*10^2:   vy:=1:

>	s:=0.2: a:=1:

>

#qpots;

3d-Darstellung des Quantenpotentials, zunächst ein Orientierungsplot

>	x:='x': x0:=100:

>	plot3d(-qpots,x=-abs(x0)..abs(x0),y=-2*y0..2*y0,grid=[20,30],axes=framed,view=-10..100);

>

Auf Details muß man warten können

>	plot3d(-qpots,x=0..abs(x0),y=-2*y0..2*y0,grid=[40,40],axes=framed,view=-10..50,orientation=[20,20]);

>

Schnitt parallel zur Verbindungslinie der beiden Zentren

>	y:='y':x:=50:

>	plot(-qpots,y=-2*y0..2*y0);

>

Zahlen des Jönsson-Experimentes (Größenordnungen). Änderung der Spaltbreite verschiebt das ganze Muster in x-Richtung!!

Große Spaltbreite -> Doppelspalt am Ort der Quelle.

>

>	unassign('x0','y0','a','t0','vx','vy','s','t','x'):

>	t0:=x0/vx:

>

t:=x/vx:

>	vy:='vy': vyb:=vy:

>	y0:=10^(-6):

>	vx:=10^8:   vy:=100:

>	s:=10^(-7): a:=10000:

>

#qpot;

2d-Schnitt

>	y:='y':x:=0.1: x0:=0.2:

>	plot(-qpots*10^(-15),y=-2*y0..2*y0);

>

Zur Orientierung (man sollte immer auch das Gebiet vor dem Doppelspalt mit untersuchen):

>	x:='x': x0:=0.2:

>	plot3d(-qpots*10^(-15),x=-x0..x0,y=-2*10^(-6)..2*10^(-6),view=-0.1..0.5,grid=[20,30],axes=framed);

>

>	x:='x': x0:=0.2:

>	plot3d(-qpots*10^(-15),x=0.01..0.3,y=-4*y0..4*y0,view=-0.1..0.5,grid=[40,40],axes=framed,orientation=[-33,36]);

>

Statt des Quantenpotentials kann auch die Wirkung (=Phase der psi-Funktion, des Propagators) selbst untersucht werden. Man erhält sie als Argument der Exponentialfunktion. Aus der Wirkung kann dann mit p=gradS das Impulsfeld berechnet werden und aus der Bewegungsgleichung (DG 1.Ordnung) die Bahn. (Die Berechnung der Bahn aus dem Quantenpotential über die Kraft und die Bewegungsgleichung 2.Ordnung überfordert Maple).

>	unassign('x0','y0','a','t0','vx','vy','s','t','x'):

Kontrolle

>

psi;

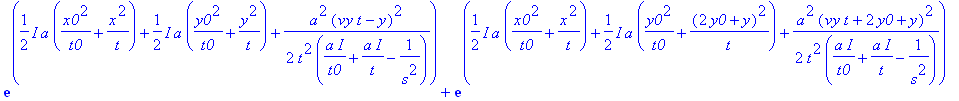
Die Wirkung ist das Argument der Psi-Funkiton

>	S:=evalc(argument(psi)):

>	Ss:=subs(y=y-y0,S):

>	t:=x/vx:  t0:=x0/vx:

>

#S;

>

Günstige Parameter:

y0:=8:

vx:=1:   vy:=0:

s:=1: a:=1: x0:=50

>	vy:='vy': vyb:=vy:

>

>

y0:=8:

>	vx:=0.1:   vy:=0:

>	s:=1: a:=10:

Iso-S-Linien

>

x0:=50:

>	cpl:=contourplot(sin(Ss),x=0..10*y0,y=-5*y0..5*y0,axes=framed,contours=5,grid=[30,30]):

>

cpl;

>

>	cp3:=plot3d((Ss),x=0..10*y0,y=-5*y0..5*y0,axes=framed,contours=5,grid=[40,40],orientation=[-40,2]):

>

cp3;

>

Lupe (auch mit -Ss darstellen!)

>	cp3:=plot3d((Ss),x=0..2*y0,y=-2*y0..2*y0,axes=framed,contours=5,grid=[80,80],orientation=[-40,2]):

>

cp3;

>

>	plot3d((Ss),x=0..2*y0,y=-2*y0..2*y0,axes=framed,contours=5,grid=[80,80],orientation=[-20,30]);

>

>

Diese Bilder geben zu denken:

Die Wirkungswellen zeigen einen Phasensprung (um Pi) von Beugungs-Maximum zu B-Maximum (quer zur Ausbreitungsrichtung der Welle). Wenn man die Wirkung selbst darstellt (ohne Sinus od. Cosinus) entstehen Sprünge im Wellenlängenabstand, weil mit "arctan(y,x)" vom Arcustangens der Hauptwert (von -Pi .. Pi) genommen wird. (Bei günstiger Perspektive bekommt man ein "Trepp-auf  Trepp-ab Bild"). Man muß sich die Oberfläche an diesen Stellen jeweils nahtlos an die Umgebung angesetzt denken. Dann entsteht eine Stufenlandschaft, bei der das zentrale Maximum am höchsten liegt und die Maxima daneben jeweils um Pi tiefer (genauer gesagt um h und das ist genau ein Quantensprung)

Will nicht mal jemand messen, was das Elektron bei diesem Sprung abstrahlt, und damit Bohm bestätigen oder widerlegen? Zu dumm, daß das Elektron nach Voraussetzung auf all diesen "Wirkungsniveaus" die gleiche Energie hat ... und auch dazwischen, also in den Beugungs-Minima, wo es sich so schnell bewegt ... also kann es wohl nur virtuell strahlen und das virtuelle Photon gleich wieder absorbieren ... war wohl nichts mit der Messung? Aber halt! man könnte ihm ja das virtuelle Photon wegnehmen ... mit einem kleinem Hohlraumresonator oder mit einem Magnetfeld oder dem Potential eines Magnetfeldes, also mit Aharonov und Bohm ... AHA-ronov-Effekt: in den Minima ist das Elektron nicht zu finden, weil es sich kurz neben den Minima Energie aus dem Vakuum borgt, bzw. zurückgibt und vor allem quer zur Beobachtungsrichtung läuft. Und wenn man nun einfach den Schirm um 90° dreht, also längs eines Minimums aufstellt? Da müßte man wohl noch die Kontinuitätsgleichung fragen. Aber was am gespenstischsten bei dieser halb kausalen Interpretation ist: das Aufstellen eines Doppelspaltes verformt das Vakuum so, daß .... usw. ... bzw. "erzeugt" ein Quantenpotential. *Wie* macht der Doppelspalt das? Aber die Welcher-Weg-Experimente zeigen ja, *daß* er es macht ... ?)

>

Der Impuls ist der Gradient der Wirkung. Wie schon die vorangehenden Bilder zeigen, gibt es Stellen, bei denen das Bohmsche Teilchen mit großer Geschwindigkeit von Maximum zu Maximum wechselt, und so interpretiert Bohm auch die Minima: die Aufenthaltsdauer ist dort gering. Die Teilchengeschwindigkeit ist übrigens "bergauf", also zu größerer Wirkung gerichtet, deshalb laufen in der Nahzone die Teilchen auch wieder zum Doppelspalt zurück: stehende Welle. (Man kann auch -Ss darstellen, das liegt der Intuition näher, die Teilchen laufen dann in den Rinnen = Beugungs-Maxima und halten sich nicht auf den Bergrücken = Beugungsminima). In der Nahzone scheint sich zu entscheiden, in welches Maximum das Teilchen sortiert wird - nach Bohm liegt es ja nur an den Anfangsbedingungen. Und wie beim Chaos können sich hier kleine Unterschiede stark auswirken. Quer zur allgemeinen Ausbreitungsrichtung ändert sich die Phase (=Wirkung) von Max. zu Max. um Pi und zwar auf  kurzer Distanz, was man aber nur bei genügend hoher Auflösung sieht.

Zur Darstellung des Impulsfeldes muß man sich ein Gebiet aussuchen, in dem keine Phasensprünge liegen, die durch die Berechnung des Arcustangens entstehen:

>	gradplot(Ss,x=5*y0..10*y0,y=-5*y0..5*y0,axes=framed);

>

Lupe

>	gradplot(Ss,x=50..55,y=-12..-8,axes=framed);

>

Zur Ergänzung noch die Darstellung des Amplitudenquadrats

>	apsi:=evalc(abs(psi)):

>	apsis:=subs(y=y-y0,apsi):

Linien gleicher Aplitude

>

x0:=50:

>	apl:=contourplot(apsis/2,x=0..10*y0,y=-5*y0..5*y0,axes=framed,contours=10,grid=[40,40]):

>

apl;

Gemeinsame Darstellung mit den Linien gleicher Wirkung

>	display({apl,cpl});

>

Also keine Orthogonaltrajektorien in den Minima, die Linien gleicher Amplitude können nicht als Bahnen interpretiert werden.

>

Amplitudenbetrag 3d

>	ap3:=plot3d(apsis/2,x=0..10*y0,y=-5*y0..5*y0,axes=framed,contours=5,grid=[80,80],orientation=[-40,2]):

>

ap3;

>

Nicht ausgereift:

>	display({cp3,ap3});

>

Numerische Berechnung von Bahnen unter Verwendung von p=gradS

>	unassign('x0','y0','a','t0','vx','vy','s','t','x'):

>	t:=x/vx: t0:=x0/vx:

>

>	vy:='vy': vyb:=vy:

>

>

y0:=8:

>	vx:=0.1:   vy:=0:

>	s:=1: a:=10:

>

x0:=50:

Kontrolle

>

#Ss;

>	with(VectorCalculus):

>	p:=Gradient(Ss,[x,y]):

>

#p[1];

Für die DGL (dx/dt=px/m, ...) müssen x und y als Funktionen der Zeit geschrieben werden.

>

t:='t':

>	p[1]:=subs(x=x(t),y=y(t),p[1]):

>	p[2]:=subs(x=x(t),y=y(t),p[2]):

>

#p[1];

Bewegungsgleichung 1.Ordnung (m=1)

>	sys:={diff(x(t),t)=p[1],diff(y(t),t)=p[2]}:

>	#sys; ######## testen: es war eine Mengenklammer zu viel

>	dsolve(sys,{x(t),y(t)},method=laplace);

Error, (in dsolve/inttrans/solveit) transform method can only be applied to linear ODE

Man kann's ja mal probieren ...

>

#vx;

Vorsicht: zu kleine Werte für x erfordern sehr große Rechenzeiten (Nahzone!)

Zu große Zeiten natürlich auch ...

>	ini:={x(0)=20,y(0)=1};

numerische Lösung in zwei Varianten

>	#printlevel:=1;

>	solp:=dsolve(sys union ini,{x(t),y(t)}, numeric,output=procedurelist); # ist default

>

#sys;

>	soll:=dsolve(sys union ini,{x(t),y(t)}, numeric,output=listprocedure);

Test

>

solp(0);

>

soll(2);

>	#plot(['solp(t)[1]','solp(t)[2]',tt=0..10]);

>	odeplot(solp,[x(t),y(t)],10..50); # Bereichsangabe ist x

odeplot begeistert nicht

>	plot([rhs(soll[2]),rhs(soll[3]),0..0.5]); #  Bereichsangabe ist t

Na ja, ... wir sind wohl an Maples Grenzen angelangt?

Geht es mit phaseportrait besser?

>	#op(1,sys);

>	with(DEtools): # Nummerierung der Gleichungen ggf. tauschen (falls Fehlermedung "must take derivative of dep. var."

# Nummerierung der Gleichungen ggf. tauschen (falls Fehlermedung "must take derivative of dep. var." oder andere Fehlermeldungen...

>	phaseportrait([op(1,sys),op(2,sys)],[x(t),y(t)],0.1..30,{[1,20,1]},scene=[x,y],stepsize=1);

Hier fängt die Numerik an ... Fortran!

>	phaseportrait([op(1,sys),op(2,sys)],[x(t),y(t)],0..10,{[0,35,5],[0,35,7]},scene=[x,y],stepsize=1);

>	phaseportrait([op(1,sys),op(2,sys)],[x(t),y(t)],0..10,{[0.1,34,7],[0.1,32,7],[0.1,30,7]},scene=[x,y],stepsize=1);

ca 25min.

>	start:=time();

>	bahnen:=phaseportrait([op(1,sys),op(2,sys)],[x(t),y(t)],0..20,{[0,30,6.6],[0,30,6.8],[0,30,7],[0,30,7.2],

>	[0,30,5],[0,30,4],[0,30,3]},scene=[x,y],stepsize=0.4):

>

bahnen;

>	(time()-start)/60.;

Immerhin sieht man bei geschickter Wahl der Anfangsbedingungen das Wechseln der Bahn von einem Maximum zum Nachbarmaximum. Aber  für eine Schar von Bahnen müßte man den Computer wohl eine Nacht laufen lassen und bekäme Probleme mit der numerischen Integration von MapleVR3, die nicht immer wieder von Null starten kann, sondern erst wieder zurückrechnen muß.

Noch eine Ergänzung zum gradplot von S. Die Komponenten des Impulsfeldes können auch 3d dargestellt werden, dann sieht man ebenfalls, wo sich das Teilchen schnell bewegt und in welche Richtung, und hat keine Probleme mit der Überbewertung des Gradienten in der Nahzone (wenn die Pfeile dort zu groß werden bleibt für die anderen Rasterpunkte in gradplot nur ein Punkt übrig):

>	px:=subs(x(t)=x,y(t)=y,p[1]):

>	py:=subs(x(t)=x,y(t)=y,p[2]):

Längsimpuls

>	plot3d(px,x=5..50,y=-30..30,axes=framed,grid=[40,80],view=-1..2,orientation=[15,15]);

>

#px;

Querimpuls

>	plot3d(py,x=5..50,y=-30..30,axes=framed,grid=[40,80],view=-2..2,orientation=[15,15]);

>

Impulsquadrat

>	plot3d(px^2+py^2,x=5..50,y=-30..30,axes=framed,grid=[40,80],view=0..10,orientation=[15,15]);

>

>

x:=50:

>	plot({px,py},y=-100..100);

>	plot({px,py},y=-1000..1000);

>

>

x:=1500:

>	plot({px,py},y=-1000..1000);

>

Winkelverteilung

>

x:='x':

>

#px;

>	pxa:=subs(x=r*cos(al),y=r*sin(al),px):

>	pya:=subs(x=r*cos(al),y=r*sin(al),py):

>

r:=10:

>	plot({pxa,pya},al=-Pi/2..Pi/2);

>

Es scheint Pole für al=+-Pi/2 zu geben, aber:

Finger weg von discont !!!!!!!!!!!!!!!!!

>

>

r:=100:

>	plot({pxa,pya},al=-Pi/2..Pi/2);

>

Das sieht nicht nach Interpolationsfehlern aus

>

>

r:=1:

>	plot({pxa,pya},al=-Pi/2..Pi/2);

>

>

r:=20:

>	plot({pxa,pya},al=-Pi/2..Pi/2);

>

Wenn Bohm recht hat, die Formel von Phillipidis et al. nicht auf unzulässigen Vereinfachungen aufbaut (z.B. "zeitunabhängiger Propagator", Vorzeichen von vy...) und dieses Worksheet keine Fehler enthält, dann haben die Elektronen unter dem Winkel 90° und in großem Abstand zum Doppelspalt große Geschwindigkeiten mit wechselndem Vorzeichen in x-Richtung und bewegen sich im Vergleich dazu nur langsam nach außen (in y-Richtung).

Könnte sein: "stehende Welle". Abhängigkeit vom Spaltabstand und der Wellenlänge?

>

r:='r':

>	plot3d([r*cos(al),r*sin(al),pxa],r=5..5000,al=-0.49999*Pi..0.49999*Pi,axes=framed,grid=[10,50]);

>

>	plot3d([r*cos(al),r*sin(al),pya],r=1..5000,al=-0.49999*Pi..0.49999*Pi,axes=framed,grid=[10,80]);

>

>	plot3d([r*cos(al),r*sin(al),pya],r=0..10,al=-Pi/2..Pi/2,axes=framed,grid=[10,80]);

>

An der Geschwindigkeit in y-Richtung sieht man schön die "fokussierende Wirkung" der Minima.

Parameter durchspielen ...

>

>	plot3d([r*cos(al),r*sin(al),pxa],r=0..10,al=-0.49*Pi..0.49*Pi,axes=framed,grid=[10,50],view=-10..10);

Schrödingergleichung

Kurzfassung

komma@oe.uni-tuebingen.de