| Wenn man nicht
genau weiß, wo sich ein Teilchen aufhält, beschreibt man es meistens
durch eine Gauß-Kurve. Und wenn es zwei Möglichkeiten gibt, wo das
Teilchen am wahrscheinlichsten anzutreffen ist, nimmt man zwei
Gaußkurven:
|
|
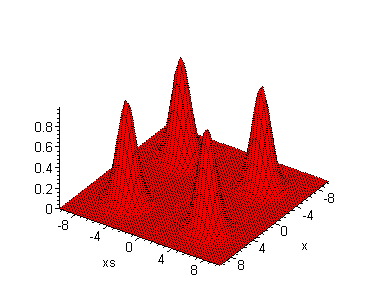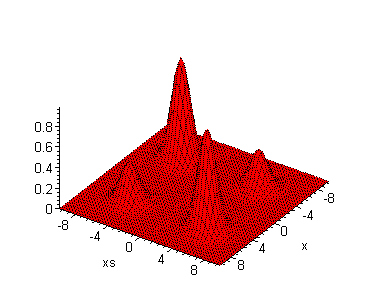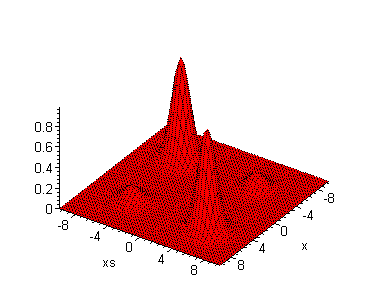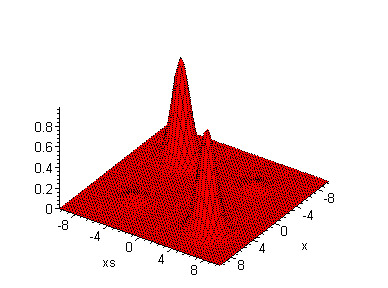
Geht man mit dieser
Beschreibung in den Phasenraum für die zwei Möglichkeiten (x,xs), so
sieht das in der klassischen Welt so aus: Zwei Gauß-Glocken auf der
Diagonalen x = xs (Dichtematrix).
|
|

|

|
| In
der Quantenwelt kommen noch zwei Glocken dazu, die auf der Nebendiagonale
liegen: Das Teilchen interferiert mit sich selbst. Allerdings kann es das
in der klassischen Welt meistens nicht lange, weil die Kohärenz
zerfällt.
|
|
|
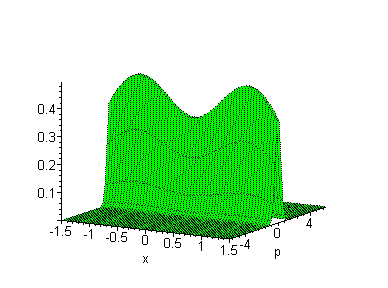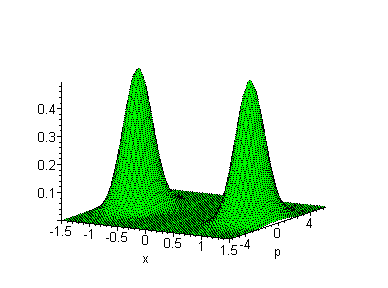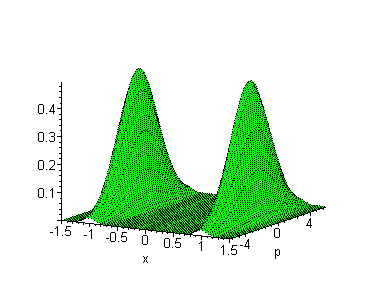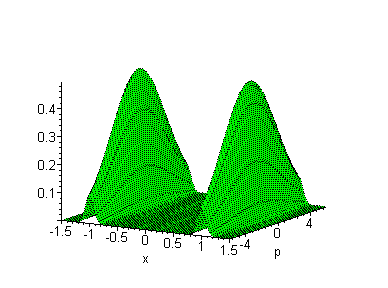
Es gibt noch andere Phasenräume, zum Beispiel (x,p). In
der klassischen Welt kann man die Breiten dx und dp der
Wigner-Verteilungen beliebig vorgeben.
|
|
In der
Quantenwelt gilt
dx*dp > h > 0
|
|

|
|
|
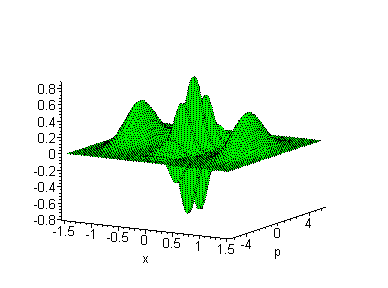
Aber die Quantenwelt hat noch mehr Überraschungen
parat: Die Zustände interferieren!
|
Egal
wie gut man das Teilchen lokalisiert - es interferiert:
|
|

|
| Und
wenn man nun h beliebig klein macht? Dann sollte man doch von der
Quantenwelt in die klassische Welt kommen und diese Interferenzen los
werden?
Sieht nicht so aus: Die Unschärfe wird kleiner, aber
die Interferenz wird größer...
|

|
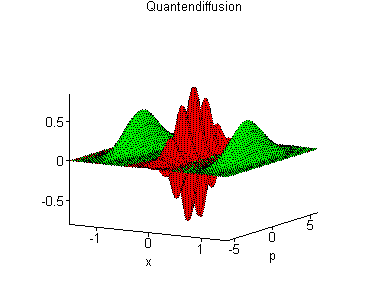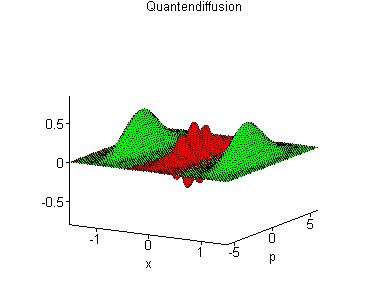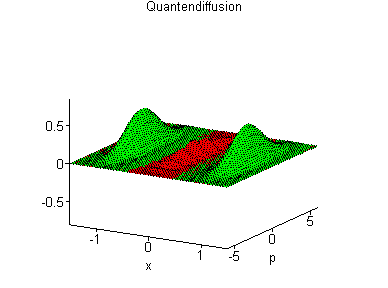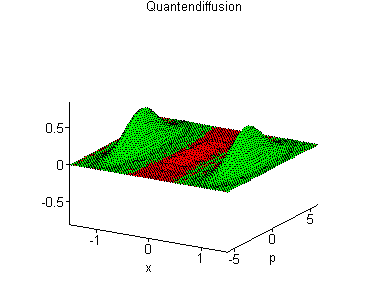
| How
long does it take?
Aber die Natur sorgt selbst dafür, dass wir unsere
klassische Welt wahrnehmen - meistens jedenfalls. Schon bei recht kleinen
Massen verschwindet die Interferenz bei Raumtemperatur sehr schnell:
Dekohärenz der Wellenfunktion.
'Moderne
Physik mit Maple'
|
|


