In den folgenden Bildern gehen von 5x5 Punkten, die äquidistant in einer Ebene angeordnet sind, gleichphasige Wellen aus (eine ebene Welle trifft senkrecht auf das Gitter). Schirmebene und Gitterebene sind parallel.
Was ist auf dem Schirm zu sehen? 49 Punkte? Warum nicht ganz äquidistant?
Dieses Bild entsteht, wenn die Wellenlänge 1/10 des Punkteabstands beträgt und der Schirmabstand das 1000-fache des Punkteabstands (Fernzone).

Schirmabstand = 200 x Punkteabstand.
Wellenlänge = 1/10..1/2 x Punkteabstand.
Wie erwartet wird die Anzahl der Haupt- und Nebenmaxima mit zunehmender Wellenlänge schließlich doch kleiner (stroboskopische Effekte ;-)).
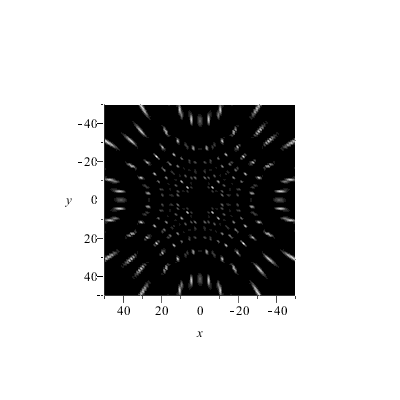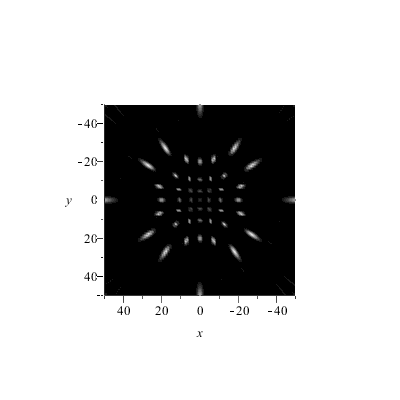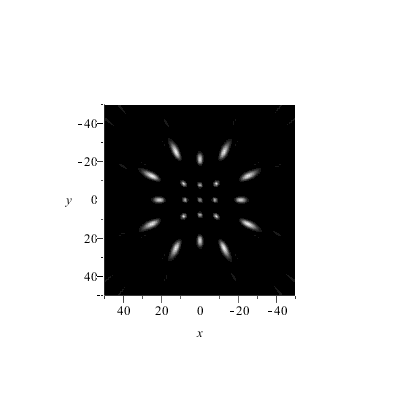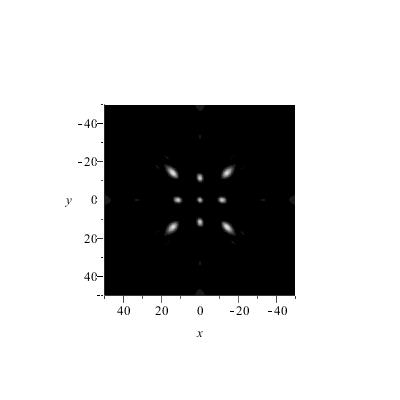
Wellenlänge = 1/10 x Punkteabstand.
Schirmabstand = 10..500 x Punkteabstand.
Können Sie das mit einem eigenen Regenschirmexperiment bestätigen, oder ist der Arm nicht lang genug?

Wellenlänge = 1/10 x Punkteabstand.
Schirmabstand = 200 x Punkteabstand (in x-Richtung).
Variiert wird der Abstand der Zentren in y-Richtung vom ursprünglichen Wert (gleicher Abstand wie in x-Richtung) bis 0 (1D-Punktgitter).
Die Animation läuft vor und zurück, damit man etwas mehr Zeit hat, die Interferenzhyperbeln (auf dem Schirm) im Umkehrpunkt zu erkennen.

Die Interferenzmaxima des Kreuzgitters liegen in der Fernzone auf (den Mantelflächen von) Kegeln (genauer auf Rotationshyperboloiden). Der Schnitt dieser Flächen mit der Schirmebene (rechts vorne) ergibt bei den gewählten Parametern zwei Scharen gleichseitiger Hyperbeln. Hauptmaxima entstehen aber nur dort, wo sich Kegel um die y-Achse mit Kegeln um die x-Achse schneiden.
y-Achse nach oben, x-Achse von rechts hinten nach links vorne, z-Achse von links hinten nach rechts vorn. Die Einfärbung dient nur der Illustration.

