Mit der Kopplungskonstanten κ gilt für die Kreisbewegung eines Elektrons im Coulombfeld:
![]()
| (1) |
also Coulombkraft = Zentripetalkraft. Wird der Drehimpuls gequantelt (erstes Bohrsches Postulat)
![]()
| (2) |
so sind nur noch Bahnen mit diesen Radien und (Kreis-) Frequenzen 'erlaubt':
![]()
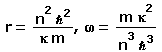
|
(3) |
Siehe Illustrationen. Bei der Bewegung im Zentralfeld ist der Betrag der gesamten Energie gleich der kinetischen Energie:
![]()
| (4) |
Also sind mit den quantisierten Werten von oben nur folgende Energien 'erlaubt' ('stationäre Zustände'):
![]()
![E[n] = `+`(`/`(`*`(`/`(1, 2), `*`(m, `*`(`^`(kappa, 2)))), `*`(`^`(n, 2), `*`(`^`(`ℏ`, 2)))))](kimages/korresp2_10.gif)
|
(5) |
Nach dem zweiten Bohrschen Postulat (Frequenzbedingung) gehören dazu die Frequenzen
![]()
| (6) |
Genau genommen ist das nicht die Frequenzbedingung, sondern Einsteins Gleichung E = h f ; die Frequenzbedingung meint die Differenz zweier solcher Frequenzen (oder Energien). Jedenfalls gilt dann für die Frequenzen:
![]()
![omega[n] = `+`(`/`(`*`(`/`(1, 2), `*`(m, `*`(`^`(kappa, 2)))), `*`(`^`(`ℏ`, 3), `*`(`^`(n, 2)))))](kimages/korresp2_14.gif)
|
(7) |
was sich allerdings von den oben berechneten Frequenzen um den Faktor n/2 unterscheidet. Stehen also die beiden Bohrschen Postulate im Widerspruch? Nein und Ja!
Nein: Sowohl Drehimpuls als auch
Energie lassen sich quantisieren.
Ja: Aber nicht mit der Bewegung klassischer Teilchen. In
seinem Artikel in Philos. Mag. 26,1 (1913) umgeht Bohr dieses Problem (Faktor n/2)
elegant mit dem Ansatz "Putting E =
(n/2) h f " (Seite 5, Gleichung 2), man sollte also n/2 den
Bohrschen Faktor nennen.
Wir bohren ein Schlupfloch aus der Misere ("Korrespondenzprinzip") und rechnen in atomaren Einheiten.
![]()
| (8) |
Dann ist die Frequenz der Überlagerung von zwei "stationären Zuständen" mit den Quantenzahlen n und n+k (Frequenzbedingung):
![]()
| (9) |
Oder für große Quantenzahlen
![]()

|
(10) |
was der klassischen Umlauffrequenz (~1/n^3, blau) 'korrespondenzmäßig entspricht' (k = 1):
![]()

|
Und die Moral von
der Geschicht? Trau den Apostulaten nicht:
Es kann keinen Quantensprung geben, weil die Frequenz der emittierten
Strahlung die Differenzfrequenz der "stationären Zustände" ist. Würde der
Übergang sprunghaft erfolgen, könnte keine Differenzfrequenz zustande kommen.
Es kann aber auch keine stationären Zustände geben, weil sonst das Elektron
springen müsste :-)).
Und der Grundzustand? Ist auch nicht zu 100% stabil (Elektroneneinfang). Man
munkelt, dass die 99,99..% der stabilen Atome durch das Vakuum stabilisiert
werden. Oder sich einfach an Bohrs Postulate halten?
Schrödingers Zusatz: Weshalb ergibt sich bei der Überlagerung von zwei Zuständen die Differenzfrequenz?
![]()
| (11) |
![]()
| (12) |
![]()
| (13) |
Also alles nur eine Schwebung? Jedenfalls ist nur die Schwebung (und damit die Superposition von "stationären Zuständen") als zeitliche Veränderung beobachtbar!
Zunächst ein paar Bohrsche Bahnen, also Kreise mit den Radien n 2.
Von 1 bis 15
 Preisfrage: zwischen welchen Bahnen findet der größte Quantensprung statt? |
und von 15 bis
50
 Preisfrage: zwischen welchen Bahnen findet der größte Quantensprung statt? |
|
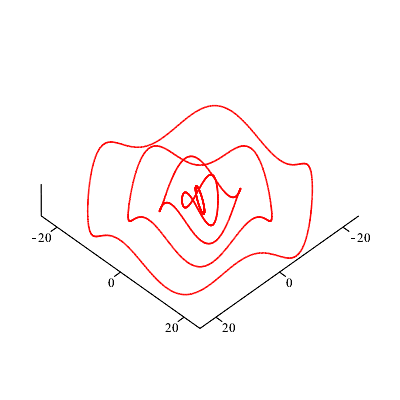
Quantisierung: Eine gängige aber falsche Erklärung für die (nicht existierenden) Bohrschen Bahnen ist, dass sich das Elektron nur auf Bahnen aufhält, deren Umfang ein ganzzahliges Vielfaches n der De Broglie-Wellenlänge des (nicht relativistischen) Elektrons ist. Manchmal liest man sogar, dass diese "stationären Zustände" stehenden Wellen entsprechen. Und "tatsächlich": Berechnet man für alle Radien die Wellenlänge des Elektrons und trägt eine Welle mit dieser Wellenlänge über dem jeweiligen Kreis auf, so ergibt sich die Fläche in Grautönen, die nur für r = n2 "den Anschluss findet" (die passende Phase hat), hervorgehoben durch die roten Kurven. Ex falso quodlibet! |

|
| Wobei es sich bei den roten Kurven um Lissajous-Figuren handelt (zur Abwechslung einmal anders dargestellt). |
|
Nimmt man zwei
solcher Bohr -
De Broglie -
Lissajou -
Wellen zu
benachbarten
"Quantenzahlen"
(50 und 51), so
ist leicht
einzusehen, dass
sich diese
Wellen auf der
einen Seite
verstärken und
auf der anderen
Seite aufheben.

|
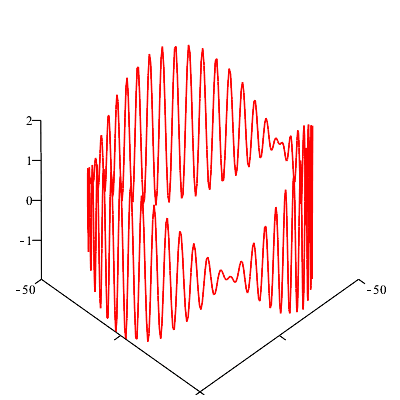
Überlagert man
unter
Missachtung
aller Verbote
beide Wellen, so
erhält man eine
Schwebung, die
man auf dem
Computer auch
laufen lassen
kann.

|
|
Man kann auch
Wellen
überlagern, die
sich in ihrer
Quantenzahl um
mehr als 1
unterscheiden...
Falls Sie diese Bilder einprägsam finden, sollten Sie sich auch einprägen, dass sie falsch sind. Ein Atom ist nicht "flach" (zweidimensional) und das Elektron ist weder punktförmig auf einer Bahn unterwegs noch kann es als eindimensionale Welle dargestellt werden. Ein etwas besseres Modell finden Sie hier. |
|
