Zum Kreispendel sagt man manchmal auch "ebenes mathematisches Pendel" und meint damit eine punktförmige Masse, die sich reibungsfrei auf einem Kreis bewegt, der im Schwerefeld "senkrecht steht" (siehe oben). Manchmal ist damit auch ein Fadenpendel gemeint, dessen punktförmige Masse sich auf einem horizontalen Kreis bewegt (wozu man meistens "Kegelpendel" sagt).

Die Differentialgleichung des hier behandelten Kreispendels lautet 

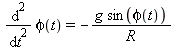(1)

und ist leider nur numerisch lösbar. Das nächste Diagramm zeigt den Winkel, die Winkelgeschwindigkeit und die Winkelbeschleunigung als Funktionen der Zeit und mit den Anfangswerten obiger Animation: Startwinkel = 0.99 π (oben rechts), Startgeschwindigkeit = 0. Welche Kurve gehört zu welcher Größe? 

Die x-Koordinate, die x-Komponenten der Geschwindigkeit und Beschleunigung, wobei die Werte der Beschleunigung halbiert sind, also x, vx, ax/2: 

Ebenso z, vz, az/4: 

Welche Beschleunigung erfährt die Masse im tiefsten Punkt? Stimmt die maximale Geschwindigkeit?

Phasendiagramme  

Zuerst die "ganz normale Bahn", also z(t) über x(t), als Probe 

Phasendiagramme periodischer Bewegungen sind immer geschlossene Kurven. Weshalb ist dann der Kreis oben nicht ganz geschlossen? 

Die Winkelgeschwindigkeit über dem Winkel: 

Damit man sich den Ablauf der "Bewegung" besser vorstellen kann, sind Punkte in gleichen Zeitschritten dargestellt. Die blaue "Bahn" gehört zum Startwinkel 90°. Obwohl die Beweungung für den (fast) vollen Startwinkel stark anharmonisch ist, ergibt sich eine cosinusförmige Kurve. Es gilt hier aber: Je harmonischer die Schwingung, desto ellipsenförmiger das Phasendiagramm. 

Winkelbeschleunigung über Winkel: 

Wer hätte das gedacht: ein "Minus-Sinus"! Wie es ja die Differentialgleichung verlangt (g = 10, R = 4, MKS (z.B.)). 

Aber das heißt wieder nicht, dass die Schwingung harmonisch ist, vielmehr gilt hier: Je harmonischer die Schwingung, desto linearer das Phasendiagramm. 

Man beachte auch: In Phasendiagrammen ist "die Kurve der Beschleunigung" nicht einfach die geometrische Ableitung der Geschwindigkeitskurve. 

Weitere Übungen zum Lesen von Phasendiagrammen. Die Achsen sind ausnahmsweise beschriftet. Wo liegt der Start- und Endpunkt der Phasenbahnen? In welchem Sinn werden sie durchlaufen? Mit welcher Geschwindigkeit? 

Aber bitte mit Pfeilen!
Grün: Geschwindigkeit, blau: Zentripetalbeschleunigung, rot: Gesamtbeschleunigung.

Wer nachrechnen will: Der Geschwindigkeitspfeil ist mit einem Viertel seiner Länge und die Beschleunigungspfeile mit einem Fünftel dargestellt (MKS-Einheiten, man vergleiche mit den Angaben und Diagrammen oben).

Diese Bewegung kann mit einem Stangenpendel (masselose Stange ohne Reibung drehbar um eine horizontale Achse) "realisiert" werden.

Nimmt man ein Fadenpendel oder eine Loopingbahn, in der die Kugel (besser: punktförmige Masse) innen gleitet, so "stürzt sie ab", wenn sie mit der hier vorgegebenen Geschwindigkeit unten startet. Wo passiert das?

Lässt man umgekehrt eine Kugel auf einem Kreiszylinder außen herabgleiten (von fast ganz oben), so "hebt sie ab". Wo?
 
Und wie würde das alles aussehen, wenn das Pendel den Überschlag schafft (=> "Siehe auch" unten...)?
Oder der Innenlooping ohne Absturz klappt?