Besonders um die Weihnachtszeit interessiert man sich dafür, wann die Tage wieder länger werden...

Die grüne Kurve zeigt den Sonnenuntergang, die rote den Aufgang und die gelbe die Tageslänge als Funktion der Jahrestage für einen Ort bei Stuttgart. [Berechnet und dargestellt mit Maple, Formeln PDF.]	(Wenn die Animationen (oben und unten, 365 frames) "zu langsam" laufen, verkleinern Sie das Fenster so, dass nur eine von beiden zu sehen ist.)

Natürlich hängt die Tageslänge vom Stand der Sonne ab.  Trägt man den höchsten Stand der Sonne (die Mittagshöhe) als Funktion der Jahrestage ab, also die Höhe (Deklination in Grad über dem Himmelsäquator) und Seite (Rektaszension ebenfalls in Grad), so entsteht eine 8: das Analemma.

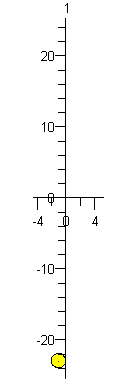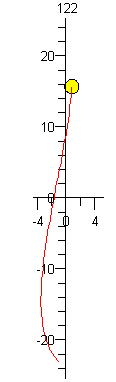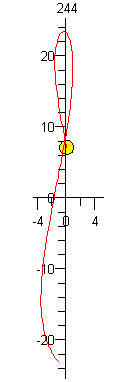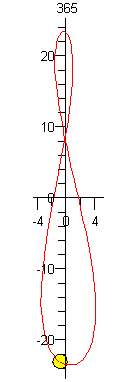
Verwendet man nicht die Mittagshöhe, sondern einen anderen Sonnenstand (zu jeweils gleicher Tageszeit), so steht die 8 nicht senkrecht:

Obige Abbildung dient nur der Illustration oder als Prinzipskizze. Sie wurde aus dem Analemma der Mittagshöhe durch Rotation um eine geeignete Achse (in Südrichtung) im Horizontsystem künstlich erzeugt. Immerhin erkennt man, dass im Laufe des Jahres die Tage länger werden (und dann wieder kürzer): An Weihnachten befindet sich die Sonne am Fuß der 8 (oder des Bowling-Pins) und im Juni an der Spitze. Auf dem 50. Breitengrad schwankt also die Tageslänge zwischen ca. 8 und 16 Stunden.

Von der Prinzipskizze zur 3D-Darstellung der Himmelskugel im Horizontsystem:

Legende: grün = Horizont, blau = Ekliptik (für Silvester 12h, nur zur Orientierung), schwarz = Meridian (und die Achsen im Horizontsystem), gelb = OW-Großkreis, rot = Himmelsäquator (und Analemmata). Dass das auf die Himmelskugel projizierte Analemma seine Lage im Laufe eines Tages ändert, sieht man in einer statischen Darstellung "nur" an der Orientierung zu den (grauen) Großkreisen der (blauen) Himmelskugel. Was unter dem Horizont liegt, ist natürlich für Beobachter auf dem 50. Breitengrad und nördlich davon nicht sichtbar, aber man kann sich ja rein rechnerisch einmal einen Blick von außen auf die "Himmelskugel" gönnen. (Hintergrundbild: Holzschnitt aus Camille Flammarion, L'Atmosphere: Météorologie Populaire. Wikimedia Commons.)

Nehmen Sie sich 81 Sekunden Zeit, um den Auf- und Untergang des Analemmas im Zeitraffer zu verfolgen [Anleitung: Die senkrechte Gerade fixieren]:

Man kann die Himmelskugel auch rechnerisch plattwalzen (Plattkartenprojektion). Dann sieht das (gedachte) Analemma im Laufe eines Tages im Stundentakt am Nordpol (90° Breite) so aus (blau = Ekliptik):

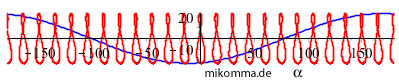
also "ganz normal", weil am Nordpol Horizontsystem und Äquatorsystem zusammenfallen. Die Sonne beschreibt je nach ihrem Stand auf der Ekliptik (fast) horizontale Kreise über dem Horizont (Polartag) oder unter dem Horizont (Polarnacht).

Der nächsten Darstellung (Breitengrad 48.5°) kann man zwar die exakten Werte des Sonnenstands entnehmen, aber es machen sich in der Plattkartenprojektion Verzerrungen der Analemmata bemerkbar:

Bei hohem Sonnenstand wird der obere Teil der 8 nach Ost oder West (Süd in der Mitte) verschoben, was bei bei 24° (nördlicher Breite) noch deutlicher wird:

Fotografierte Analemmata (dazu muss man ein Jahr lang jede Stunde eine Aufnahme machen, wenn die Sonnen zu sehen ist :-)), zeigen diese Verzerrungen nicht.

Zum Schluss noch eine Reise vom Nord- zum Südpol auf der Plattkarte:

Die Animation springt vom Süd- zum Nordpol zurück, bzw. die Bowling Pins werden vom Kopf wieder auf die Füße gestellt. Das ist aber kein Quantensprung!

Alles klar?

Links: Tageslänge und Analemma | Der schielende Mond | Venuszyklus | Lagrangepunkte, stabile Orbits und Trojaner