Man liest oft, dass Photonen Klumpen bilden können (bunching) oder Abstand halten können (antibunching) und dass es auch Photonen gibt, die sich "so gut wie klassisch verhalten" (kohärentes Licht). Dazu wird eine "Photonenverteilung" gezeigt, die die Wahrscheinlichkeit für n Photonen (zu welcher Zeit an welchem Ort?) angibt und daneben ein "Strichcode", der die zeitliche Abfolge der Photonen oder die "Photonenstatistik" (an welchem Ort?) symbolisieren soll, etwa so: 

Photonenverteilung

Photonenstatistik

Und der mitdenkende Leser muss sich fragen, woher der kühne Schluss von einer Verteilung über n auf eine Verteilung über t kommt.

Das "Maß aller Dinge" für die Photonenstatistik ist dabei die Poissonverteilung: Photonen, die einer Poissonverteilung "gehorchen", bilden weder Klumpen noch halten sie Abstand. Wenn die Verteilung breiter ist (Super-Poisson) gibt es Klumpen und wenn sie schmaler ist (Sub-Poisson), halten die Photonen Abstand. So liest man. 

Dieser Artikel soll etwas Licht auf die Problematik solcher verkürzten Darstellungen werfen. 

Zunächst muss man eine Verbindung zwischen der "zeitlosen Photonenverteilung" (alleine als Funktion der Photonenzahl n) und ihrer zeitlichen Entwicklung herstellen. Hat man einen "stationären Photonenstrom" mit der mittleren Photonenrate <w> , so gilt für die mittlere Zahl <n> der Photonen, die in der Zeit  (genauer im Zeitintervall) t registriert werden können (siehe Literatur, Glauber):

(1)

Damit sieht eine mehrdimensionale Poissonverteilung p(n,t) so aus (<w>  wird in den folgenden Formeln als w notiert),

Laserlicht oder kohärentes Licht:

>	pois:=(w*t)^n/n!*exp(-w*t);

 

(2)

  

>	plot3d(pois,t=1..5,n=0..10,axes=normal,color=red);

 

Das heißt, der Mittelwert der Verteilung verschiebt sich mit t und die Verteilung wird breiter. Die 2D-Darstellung der Kurvenschar mit t als Parameter ist etwas übersichtlicher: 

>	plot([seq(op([pois]),t=[1,2,3,4,5,6,7])],n=0..30,color=red);

 

Nimmt man eine geometrische Verteilung (thermisches Licht), so erhält man: 

>	ch:=1/(1+w*t)*(w*t/(1+w*t))^n;

 

(3)

 

Vergleich der Verteilungen (Laser rot, thermisch blau):

>	plot([seq(op([pois,ch]),t=[1,2,3,4,5,6,7])],n=0..30,color=[red,blue]);

 

Nun sagt man: die geometrische Verteilung (Bose-Einstein-Statistik) ist wesentlich breiter als die Poissonverteilung (Super-Poisson), was die Ursache für Bunching sei, oder auch: "Bosonen mögen sich" und bilden deshalb Klumpen. 

Das ist aber ein Trugschluss (in mehrfacher Hinsicht)! Die zeitliche Abfolge der Registrierung von Photonen wird alleine durch p(n=0,t) bestimmt, genauer gesagt ist sie zur zweiten Ableitung dieser Funktion nach der Zeit proportional. Die Verteilung über n spielt darin jedenfalls keine Rolle. Geht man von einem Idealexperiment aus, in dem auch die Statistik der Registrierung (Ansprechwahrscheinlichkeit der Detektoren, usw.) keine Rolle spielt, so hat man die Dichte für die bedingte Wahrscheinlichkeit w(t) zu berechnen, dass das erste Photon zur Zeit 0 (allgemeiner t0) und das zweite zur Zeit t (allgemeiner t0+t) registriert wird.

Für kohärentes Licht erhält man:

>	wco:=w*exp(-w*t);

 

(4)

 

Das ist in diesem Fall gleich p(n=0,t): Laserlicht ist nicht nur kohärent, sondern seine Photonen sind auch "statistisch unabhängig" (exponentielles Abklingen wie beim radioaktiven Zerfall)!

Für thermisches Licht erhält man: 

>	wch:=2*w/(1+w*t)^3;

 

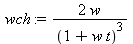
(5)

 

Entstehen die Photonen durch Resonanzfluoreszenz (z.B.), so kann man ohne die Kenntnis einer Photonenverteilung über n die entsprechende Wahrscheinlichkeitsdichte so angeben:

>	wantib:=diff((1-exp(-3/2*w*t))^2,t);

 

(6)

 

Diese Funktion w(t) gibt in stark vereinfachter Form die Photonenrate im Experiment von M. Dagenais und L. Mandel (1978, siehe Literatur) wieder und entspricht der Statistik einer radioaktiven Zerfallsreihe (Aktivität des Tochterkerns).

Im Vergleich sehen diese zeitlichen Verteilungen w(t) so aus (<w> = 2(passende Einheiten)):

>	plot([wco,wch,wantib],t=0..2,color=[red,blue,black]);

 

Nun "sieht man":

• Laserlicht (rot): w(0) ist gleich <w> und w(t) klingt exponentiell ab.

• thermisches Licht (blau): w(0) ist gleich 2*<w> und w(t) unterschreitet für größere t die "Laserverteilung". D.h., die Registrierung von Photonenpaaren ist in kleinen Zeitabständen wahrscheinlicher als in großen: Bunching!

• Fluoreszenzlicht (schwarz):  w(0) ist gleich 0 (!) und w(t) hat ein Maximum (das über den anderen Verteilungen liegt), D.h., die Registrierung von Photonenpaaren ist in kleinen Zeitabständen sehr unwahrscheinlich und in bestimmten Zeitabständen am wahrscheinlichsten: Antibunching!

Und wie kann man das veranschaulichen?

In nebenstehender Abbildung ist die Zeit der Registrierung eines Photons über der Anzahl der Registrierungen für <w> = 10(passende Einheiten) abgetragen: Wenn man demnächst "Photonen on demand" erzeugen kann, und dies mit einer konstanten Rate macht, so liegen die Zeiten der Erzeugung und Registrierung auf einer Geraden (grün). (Das wäre also der wirklich klassische Fall, hier nur zur Orientierung eingezeichnet ;-)). Die Registrierungszeiten von "Laserphotonen" (rot) schwanken "statistisch unabhängig" um eine konstante Zählrate. (Das sieht man doch - oder?) Die Registrierungszeiten von "thermischen Photonen" (blau) schwanken nicht "statistisch unabhängig" um eine konstante Zählrate. Manchmal dauert es ziemlich lange bis das nächste Photon registriert wird (fast senkrechte Linien). Aber die thermisch Quelle füllt diese Lücken durch Bunching wieder auf. Die Registrierungszeiten von "Fluoreszenzphotonen" (schwarz) liegen der konstanten Zählrate am nächsten. Welches Licht ist nun "klassisch" und welches "nicht klassisch"?
Vielleicht helfen ein paar Statistiken? Stellt man die Registrierungszeiten von Laserphotonen als "Strichcode" dar (rot), so sieht man eigentlich nicht viel. Wenn die Striche dicht liegen (zusammenhängende rote Rechtecke), muss das keine besonders hohe Zählrate bedeuten. Vielmehr kann sich in dieser Darstellung unter einem einzigen Strich die Registrierung mehrerer Photonen verbergen, die in besonders kurzen Zeitabständen erzeugt wurden. Ein Histogramm (schwarze Linien) ist etwas aussagekräftiger. Wenn man die Anzahl der Registrierungen in einem (geeignet kleinen) Zeitintervall aufsummiert, zeigen die Spitzen des Histogramms eine höhere Dichte besser an als der "Strichcode". Alles nur eine Frage der Auflösung ;-). Zur Orientierung ist wieder der "klassische Mittelwert" (grün) eingetragen.
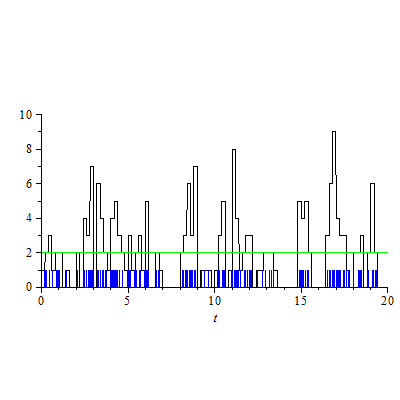
Wie sieht in dieser Darstellung die Statistik für thermisches Licht aus? Also da sind schon Bündel (oder Klumpen?) zu sehen! Wobei natürlich die Lücken mindestens ebenso wichtig sind!
Und Fluoreszenzphotonen scheinen tatsächlich etwas mehr Abstand zu halten als Laserphotonen, wenngleich sie vom idealen Antibunching (äquidistante Striche, Histogramm  = Mittelwert) noch etwas entfernt sind. Anmerkung: "Fehlende" horizontale Linien des Histogramms werden durch die grüne Linie des Mittelwerts überdeckt (gilt auch für obige Histogramme).

Man sollte aber über all der Statistik die Physik nicht vergessen: "Photonen an sich" haben - physikalisch gesehen - keine Statistik (oder Verteilung?), die sich direkt bestimmen lässt. Es kommt vielmehr darauf an wie sie entstehen und nachgewiesen werden. Man kann zwar Photonenstatistiken (oder die Statistik des quantisierten elektromagnetischen Feldes) nachträglich manipulieren, aber in erster Linie handelt es sich bei einer "Photonenstatistik" um die Statistik der Quellen und Absorber von Photonen. Die Photonen sind und bleiben "nur" Botenteilchen.

Insofern sind auch solche sprachlichen Gebilde etwas irreführend (Zou und Mandel 1990,  Literatur):

Photonen (und andere Teilchen) haben keine Neigungen, sich wie ein Kollektiv oder wie Individuen zu verhalten. Natürlich wissen Zou und Mandel, was sie sagen. Und die meisten Physiker verstehen auch diese anthropozentrische Sprechweise und denken automatisch die Anführungszeichen an der richtigen Stelle mit: "the tendency of photons to distribute "themselves" preferently". Aber wer diese Aussage wörtlich nimmt, überliest dann auch gerne, dass das Photon "auf einen Detektor treffen" muss, wenn es zur "Photonenstatistik" beitragen soll, und vergisst komplett wie es erzeugt wurde.

Bei der folgenden eindeutigen Aussage (Zou und Mandel 1989) muss man allerdings keine Anführungszeichen mitdenken: