Dreieckblende

Das Standardbeugungsobjekt im Physikunterricht ist ein Spalt, der mit seinen parallelen Kanten parallele Interferenzstreifen erzeugt (wenn er voll ausgeleuchtet wird).

Wenn man statt des Optik-Standard-Spaltes ein Dreieck nimmt, sollte sich an der Beugungsfigur etwas ändern.

Wie sieht nun das Beugungsmuster aus? Schauen Sie einmal nachts durch eine Kamera mit passender Blende auf eine Straßenlaterne!

Ein gleichseitiges Dreieck erzeugt diese Beugungsfigur. Weshalb? Intensität in logarithmischem Maßstab, Fraunhoferbeugung.

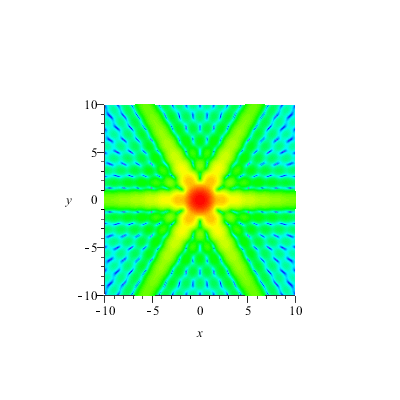Mit künstlicher Einfärbung ist das eigentlich schöner! Wir merken uns also die Farbskala: "immer dem Regenbogen entlang".

In den folgenden Animationen wird das Dreieck verändert. Wie?

Anmerkungen:

• Beugung: Abweichen der Strahlen vom geometrischen Strahlengang (Wellenoptik statt Strahlenoptik).

• Interferenz: Zusammenwirken mehrerer Wellen (oder Strahlen :-) durch Superposition der Amplituden.

• Huygenssches Prinzip: Jeder Punkt einer Wellenfront kann als Zentrum einer Elementarwelle betrachtet werden.

• Methode: Eine endliche Öffnung hat unendlich viele Punkte, es interferieren also unendlich viele Elementarwellen. Zur Berechnung der resultierenden Amplitude (und Intensität)  muss also integriert (statt summiert) werden. Leider entstehen dabei Integrale (-> Kirchhoff), die sich "nicht ganz einfach" auswerten lassen, bzw. viel Rechenzeit kosten. Obige Darstellungen wurden für die Fernzone ("Fraunhoferbeugung") berechnet.

Noch eine andere Methode:

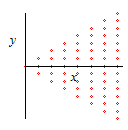
Man kann die Blende (mit unendlich vielen Elementarzentren) durch eine passende Anordnung endlich vieler (z.B. 64) Elementarzentren ersetzen.		Dann die Amplituden der Elementarwellen addieren (Vielstrahlinterferenz) und quadrieren. Sieht doch ganz vernünftig aus?
Aber was passiert hier?
Und hier?
	Keine Sorge! Ihr Rechner ist nicht langsam. Die Animationen werden nur langsamer abgespielt, damit Sie alles in Ruhe beobachten können...