|

Quelle:
https://commons.wikimedia.org/wiki/File:Earth-Moon_System.jpg
From 4 million miles away on December 16, 1992,
NASA's robot spacecraft Galileo
took this
picture of the Earth-moon system.
Schielt der Mond? Natürlich nicht - er hat ja
nicht zwei Augen!
Dennoch liest man z.B.:
"Schielt der Mond?
Die Mondsichel weist stets exakt zur Sonne –
so muss es sein, weil sich Licht geradlinig
ausbreitet. Doch manchmal schert sich die
Natur nicht darum!"
Von H. Joachim Schlichting,
SPEKTRUM DER WISSENSCHAFT Oktober 2012.
Oder in "Der Silberblick des Mondes und die
Zentralperspektive",
UDO BACKHAUS - HANS JOACHIM SCHLICHTING,
MNU Journal - Ausgabe 4.2017 - ISSN 0025-5866:
"Der aufmerksame Beobachter stößt, wenn er die
Entstehung der Phasengestalt glaubt verstanden
zu haben, allerdings auf ein Problem: Die von
der Sonne beleuchtete Mondseite scheint oft
nicht in Richtung Sonne zu »blicken«, sondern
mehr oder weniger deutlich oberhalb an ihr
vorbei zu »schielen«. Genauer: Wenn man die
Symmetrieachse der Phasengestalt geradlinig
verlängert, scheint die Linie nicht auf die
Sonne zu treffen. Sie verfehlt die Sonne umso
weiter, je größer der Winkel zwischen dem
zunehmendem Mond und der Sonne wird.
Dennoch ist das Phänomen immer wieder Gegenstand
von Publikationen, in denen es aus
astronomischer, wahrnehmungspsychologischer
und lebensweltlicher Sicht beschrieben
wird (z. B. GLAESER, 2009 und SCHOELKOPF, 1998,
STEINRÜCKEN,o. J., SCHOTT, o. J., MAYER, o. J.,
FEUERSTEIN, 2013). In einigen
dieser Arbeiten wird allein schon durch die
Komplexität der
Darstellung der Eindruck erweckt, das Phänomen
sei kompliziert und nur schwer erklärbar, in
anderen Äußerungen (BUTH,
2011, OBERSCHELP, 2012) zeigen sich
grundsätzliche Verständnisschwierigkeiten."
Die anthropozentrische Sprache (der Mond
schielt, die Mondseite blickt, die Linie
trifft,...) in manchen Artikeln ist immer
wieder faszinierend! Ist sie am Ende der
Grund für "grundsätzliche
Verständnisschwierigkeiten"?
Die Wurzeln dieses Scheinproblems reichen
übrigens (mindestens) zurück
bis zu Martin Wagenscheins "Der Mond
und seine Bewegung". Zitat:

«Hat man aber einmal das „Spähen
nach den Strahlen der Sonne“ gefunden (exakt
gesprochen: dass das auf der Verbindungssehne
der beiden Spitzen der Mondsichel errichtete
Mittellot immer auf die Sonne zielt) und hat man
einmal die ungeheure Möglichkeit zu denken
gewagt, dass der Mond ein „Ding“ sei, eine
Kugel, gemacht aus „Erde“, so kann angesichts
des Abendhimmels von Abb. 1 [s.o., kopiert aus
"Der Mond und seine Bewegung" und mit
zwei Kommentaren versehen] das Entscheidende
geschehen: die Himmelsglocke bricht zusammen,
der Mond schwebt „vorn“ und die Sonne sinkt in
einen tiefen Abgrund in den Raum zurück, wobei
sie sich zu furchtbarer Größe aufbläht. Dies
kann das Erlebnis eines Augenblicks sein. Es
kann niemals „gelernt“ werden. Jeder muss es
einmal vor dem Himmel als eine Erschütterung
erfahren, wenn er wirklich aufnehmen will, was
er „weiß“.»
Der Versuchung, diese "Didaktik der Physik"
(oder "Lyrik der Physik"?) mit weiteren
Kommentaren zu versehen, kann man kaum
widerstehen. Aber wir kümmern uns besser um die
Fakten der Physik, die übrigens auch bei
Wagenschein zu finden sind, aber so
verklausuliert, dass sie bei manchen Autoren
"grundsätzliche Verständnisschwierigkeiten"
hervorrufen.
Die Lösung des Scheinproblems
Wir nähern uns dem "Problem des schielenden
Mondes" von außen: Jede Kugel, die in etwa die
gleiche Entfernung wie die Erde von der Sonne
hat, zeigt die gleiche Schattengrenze
(Terminator) wie im Bild von NASA's robot spacecraft
Galileo. Dabei ist mit "jede Kugel" z.B. Erde,
Mond, Wolke, Ballon, Tischtennisball,...
gemeint, und mit "in etwa" der Radius der Mondbahn.
Zunächst erscheint eine Animation angebracht,
die die Größenverhältnisse veranschaulicht:
Der Durchmesser der Sonne beträgt ungefähr das 1,8-fache des Durchmessers
der Mondbahn. Der Abstand Erde-Sonne ist ungefähr 400 mal so groß wie der
Abstand Erde-Mond. Sonne und Mond haben von der Erde aus betrachtet den
gleichen scheinbaren Winkeldurchmesser.
Wenn wir den Mondbahnradius als Einheit nehmen, und sich die Erde im
Ursprung befindet, dann befindet sich der zunehmende Halbmond bei +1
und der abnehmende Halbmond bei -1 auf der Hochachse. (Preisfrage: wie groß
sind in diesem Maßstab die Durchmesser von Erde, Mond und Tischtennisball?)
Wir versuchen es mit einer kleinen Animation: Weil von der Erde aus gesehen
die Sonne gleich groß erscheint wie der Mond, sollte die Sonne auf
der Rechtsachse bei 1 stehen, und der zunehmende Halbmond nicht "waagrecht
nach rechts blicken", sondern "diagonal nach unten" (bei Sonnenuntergang).
Dann gäbe es aber weder Erde noch Mond, weil die Sonne eine Kugel ist. Wir
beginnen deshalb die Animation bei 2,5 und stellen nur den Durchmesser der
Sonne dar, sowie die Lichtstrahlen der Sonnenscheibe, die Erde und
Mond erreichen.
Der Abstand der Sonne wird oben angezeigt. Von
2,5 bis 20 geht es im Sekundentakt. Dann mit 1/10s weiter zu einem Zwischenstopp bei 100 (1s),
und wieder mit 1/10s weiter bis zum tatsächlichen Abstand der Sonne (400, 2s). |
Von der Zentralperspektive zur Parallelperspektive
 |
Was lernen wir daraus?
1. Die Sonne ist sehr groß und sehr weit entfernt. Wenn sie untergeht,
"steht" sie nicht am Horizont (Entfernung ~100km), sondern "viel weiter
weg".
2. Die Lichtstrahlen der Sonne, die Erde und Mond treffen, sind praktisch
parallel. (Rechenübung: Unter welchem Winkel erscheint der Durchmesser der
Mondbahn von der Sonne aus gesehen?)
3. Der Abstand der Lichtstrahlen der Sonne, die Erde und Mond erreichen,
beträgt bei Halbmond einen Mondbahnradius und bei Neu- und Vollmond kann er
Null werden (Finsternisse).
Klingt alles banal, aber so ist es! Aber weshalb ist dann das "Phänomen des
schielenden Mondes immer wieder Gegenstand von Publikationen"? Dafür gibt es
ebenfalls einen banalen Grund: "Die Symmetrieachse der Phasengestalt",
also der Umriss (2D) wird
gleichgesetzt mit der Symmetrieachse der beleuchteten Mondhalbkugel
(3D):
"Die Mondsichel weist stets exakt zur Sonne – so muss es sein, weil sich
Licht geradlinig ausbreitet?"
Ja, Licht breitet sich geradlinig aus. Aber die "Mondsichel" (oder
Phasengestalt) ist eine Projektion einer mit parallelem Licht beleuchteten
Kugel auf eine Ebene senkrecht zur Blickrichtung des Beobachters. Da helfen
auch keine "Beweisfotos" (Panorama, oder Fischauge), oder Tipps zum
"gekrümmten Lichtweg entlang der Ekliptik" mit vom Mond zur Sonne gespannten Schnüren oder
Drehen des Kopfes um "geeignete Achsen".
|
Um den 2D -> 3D Trugschluss zu veranschaulichen, umrunden wir den Mond in
Gedanken oder mit einem Orbiter. Wenn wir das in der Ebene der Ekliptik tun
(und der Mond auch in dieser Ebene steht, wie im Folgenden immer
angenommen), sieht das wie in nebenstehender Animation aus.
Die Darstellung ist leicht gekippt, um die Ekliptikebene (x-y-Ebene,
grau) anzudeuten.
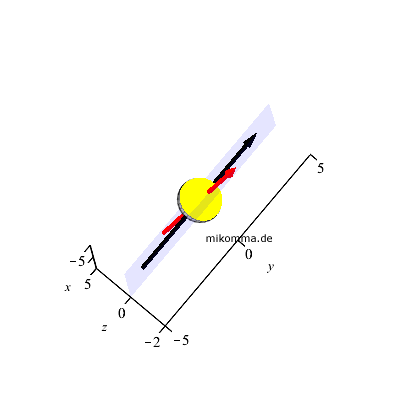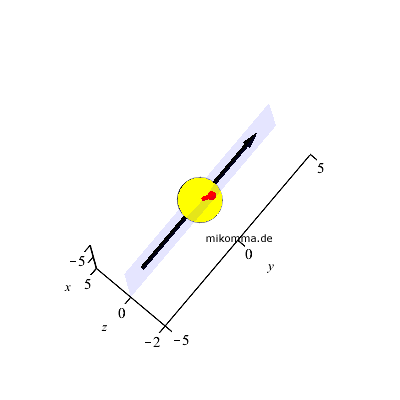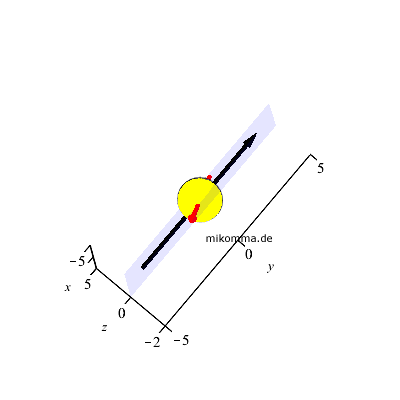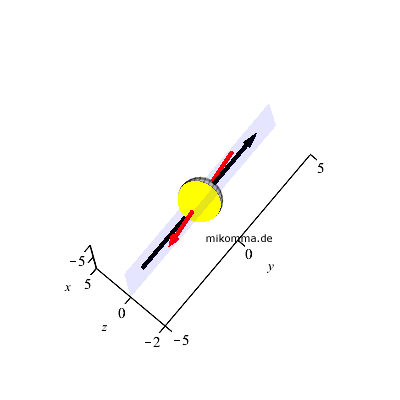
Der schwarze Pfeil gibt die Richtung der Symmetrieachse der Phasengestalt
(2D) an (er könnte auch nach links zeigen). Der rote Pfeil zeigt zur Sonne
(3D). Natürlich müssen beide Pfeile immer in der Ekliptikebene liegen, aber
der schwarze Pfeil muss nicht immer mit dem roten identisch sein, mit einer
Ausnahme: "Halbmond". Dann zeigen beide Pfeile nach rechts, bzw. auf der
Erde nach Westen (bei zunehmendem Halbmond im Frühjahr oder Herbst). Das ist auch in Ordnung so, weil
sich in diesem Maßstab (Monddurchmesser = 2) die Sonne bei ihrem Untergang
(von der Erde aus gesehen) "am Ende der y-Achse" befindet (bitte
nachrechnen, wo genau :-).
Bei Halbmond stimmt also die Aussage "Die Mondsichel weist exakt zur Sonne"
(aber nicht stets!). Aber genau dann scheint der Mond ja "weit über die
Sonne zu blicken" (je nach Jahreszeit mehr oder weniger weit). Aber ich
garantiere Ihnen: Wenn die Schattengrenze einer von der Sonne beleuchteten
Kugel (egal in welcher Höhe über dem Horizont) genau senkrecht steht, dann
müssen Sie sich nur um 90° drehen, um die Sonne am Horizont (in 0° Höhe) zu
sehen. |
 |
Wie sieht der 2D -> 3D-Trugschluss bei Neumond aus? Die Animation beginnt
kurz vor Neumond mit der abnehmenden Mondsichel und endet kurz nach Neumond
mit der zunehmenden Mondsichel.
Bei Neumond oder bei Mondfinsternis steht die Sonne sicher hinter dem Mond
(in Richtung des roten Pfeils. Ich glaube nicht, dass sie von dort "nach
rechts unten" (in Richtung des schwarzen Pfeils) springt, wenn der Mond an
ihr vorbeizieht.
D.h., gerade dann, wenn der Mond nicht "schielt", weicht die Richtung der
Lichtstrahlen, die den Mond erreichen (3D) besonders stark, nämlich um 90°,
von der "Blickrichtung" des Mondes ab.
|
 |
|
Den Neumond sieht man nicht. Aber bei
Vollmond (und kurz davor oder danach), ist eigentlich jedem klar, dass
das Licht der Sonne nicht einen krummen Weg "entlang der Ekliptik" nimmt,
sondern die Sonne geradeaus hinter dem Betrachter des Vollmonds steht. Wer
also bei aufgehendem (fast) Vollmond die Sonne sucht, sollte sich besser
nicht den Hals bei der Drehung um eine geeignete Achse verrenken, wenn er
der "Blickrichtung des Mondes entlang der Ekliptik" folgt, sondern sich
einfach umdrehen. |
 |
Wir versetzen uns noch einmal in Gedanken in "NASA's robot spacecraft Galileo",
und nehmen an, dass sich innerhalb von zwei Wochen der Blickwinkel auf den
Mond nicht wesentlich ändert. Dann würden die nebenstehenden Aufnahmen
des Mondes entstehen, und die im Ursprung des Koordinatensystems gedachte Erde hätte
die gleiche Phasengestalt wie der Mond.
Von der Erde aus gesehen kann die Symmetrieachse der Phasengestalt des
Mondes aber in viele Richtungen zeigen, je nachdem, wo der Beobachter auf
der Erde steht. Nehmen wir an, der Beobachter steht bei Sonnenuntergang auf
der x-y-Ebene (= seine Horizontebene), dann sieht er die Sonne "am Ende der
y-Achse". Bei Neumond blickt er auf die nicht beleuchtete Halbkugel des
Mondes, und bei Vollmond sieht er die beleuchtete Halbkugel. Kurz vor oder
nach Neumond oder Vollmond steht aber die Symmetrieachse der Phasengestalt
fast senkrecht auf der y-Achse, also der Richtung der Lichtstrahlen.
Bei Halbmond liegt die Blickrichtung auf den Mond genau in der Ebene der
Schattengrenze (von Mond und Erde), auf der die Lichtstrahlen der Sonne
(praktisch) senkrecht stehen. Die Symmetrieachse der Phasengestalt und die
Richtung der Lichtstrahlen stimmen überein und verlaufen in knapp 400000km
Abstand (praktisch) parallel zur y-Achse, "zeigen also weit über die Sonne,
die am Horizont untergeht".
Sie vermissen eine Mondsichel? Dazu müssen Sie sich nur vorstellen, wie der
Mond z.B. im ersten Sechstel der Darstellung vom Ursprung aus betrachtet
aussieht :). Oder Sie nehmen einen Tischtennisball, beleuchten ihn mit einer
Schreibtischlampe, und betrachten ihn aus allen möglichen Richtungen :)). |
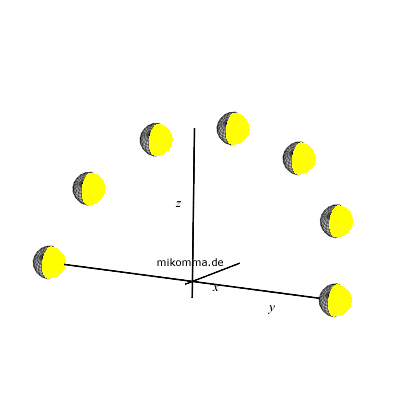 |
Mit anderen Worten (die roten Pfeile zeigen zur Sonne): Wenn es richtig wäre, dass die Sonne "entlang der
Ekliptik zu finden ist", dann hätte Galileo im Laufe zweier Wochen diese
Aufnahmen gemacht, bzw. obiger Beobachter würde immer nur den Halbmond (oder den halben
Mond?) sehen:
Seht ihr den Mond dort stehen?
Er ist nur halb zu sehen,
und ist doch
rund und schön.
So sind wohl manche Sachen,
die wir getrost belachen,
weil unsre Augen sie nicht sehn. |
 |
"Am überzeugendsten ist schließlich eine Schnur, die man so vor die Augen
spannt, dass sie Mond und Sonne scheinbar verbindet. Diesmal – man muss es
selbst gemacht haben, um es zu glauben – verschwindet das „Schielen“ auf
einen Schlag." (Schlichting, H. Joachim. In: Spektrum der Wissenschaft
43/10(2012), S. 46-48)
Vielleicht hilft beim Spannen von Schnüren, dem Verbiegen von Lichtstrahlen
oder beim Übergang von der Zentralperspektive zur Parallelperspektive bei
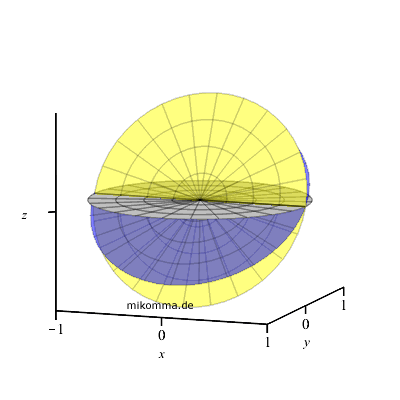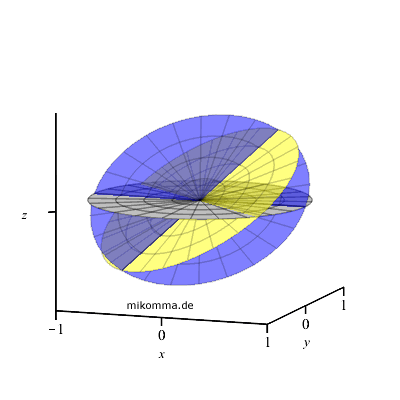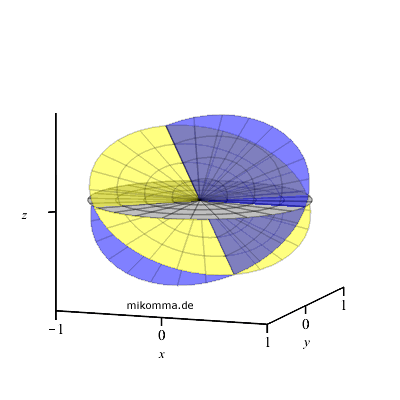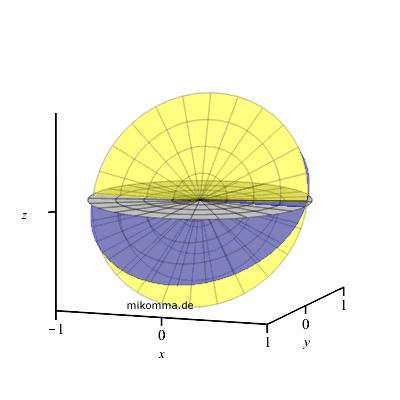
geeigneter Nick- und Drehbewegung ja auch nebenstehende Animation für 50°
nördlicher Breite:
Im Laufe eines Tages bewegt sich die Ebene der Ekliptik (gelb). Zur
Orientierung ist noch die Äquatorebene (blau) und die Horizontebene (grau)
dargestellt.
Auf anderen Breitengraden sieht das anders aus, siehe unten. |
 |

|
 |
Hier ist noch ein Beweisfoto. Wenn man es vergrößert, sieht man auch den
Mond dort stehen.
Und wo steht die Sonne? |
 |
Weitere
Scherzfragen: Am 16.07.19 sah der Mond zu später Stunde so aus.
Wo stand die Sonne? Und die Erde? Und der Fotograf?
Alle "grundsätzlichen Verständnisschwierigkeiten" beseitig? |
 |
© 2019 mikomma.de (VGWORT) 
Links:
Analemma
|
Venuszyklus |
Sternfunkeln |
Lagrangepunkte, stabile Orbits und Trojaner
|
Dieter Hildebrandt
|


