Das gängige Modell, mit dem man "Photonenbunching" thermischer Quellen erklärt, beruht auf Stoßverbreiterung:
Viele Atome strahlen statistisch unabhängig ebene Wellen gleicher Frequenz beliebig lange ab, werden aber durch elastische Stöße gestört, was zu Phasensprüngen führt. Die Amplituden aller Wellen überlagern sich und man misst die Intensität (das Betragsquadrat) der resultierenden Welle (Mittelung durch Detektor). 

In einem Gas ist die Zeitdifferenz zwischen zwei Stößen exponentiell verteilt (die Fouriertransformierte ist ein Lorentzspektrum). Das folgende Histogramm gibt ein Sampling mit Umfang 1000 wieder.

Eine ebenfalls beliebte Darstellung ist der "Strichcode":

Wenn man die Zeitdifferenzen aufsummiert, erhält man die Zeitpunkte der Phasensprünge eines Atoms:  

Nachdem die Zeitpunkte der Phasensprünge ausgelost wurden, muss noch der Betrag der Phasensprünge ausgelost werden (gleichverteilt im Intervall [0,2π]): 

Dann sehen die Phasensprünge eines Atoms so aus: 

Und die von einem Atom abgestrahlte Welle so: 

Lupe: 

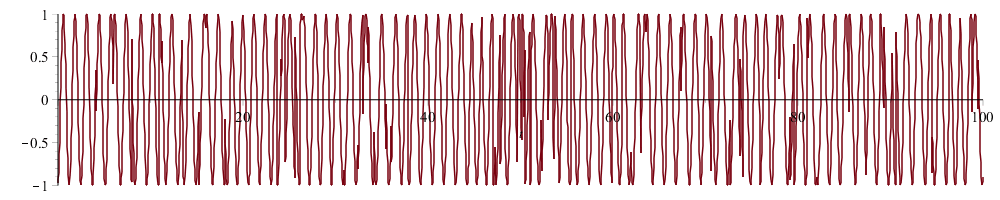
Summiert man z.B. 100 solcher Wellen mit jeweils (unabhängigen) 50 Phasensprüngen auf und bildet das Betragsquadrat (die Intensität), so erhält man eine 

Zeitreihe: 

Eine Vergrößerung

zeigt den fraktalen Charakter von "chaotischem Licht". Das Licht thermischer Quellen hat also "Klumpen auf verschiedenen Skalen", weil die endlos strahlenden Atome Phasensprünge machen, die zeitlich exponentiell abfallend verteilt sind.  

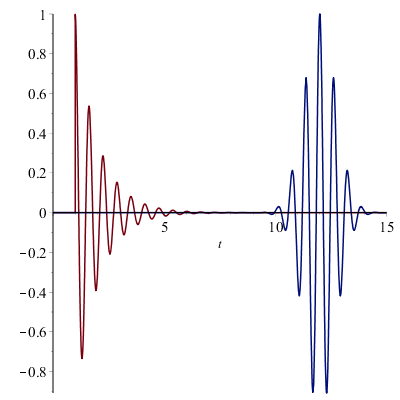
Aber Atome strahlen doch nicht endlos! Sie machen doch unvorhersagbare, ja sogar absolut zufällige Quantensprünge mit exponentiell abnehmender Wahrscheinlichkeit? Dann ist es schon verwunderlich (um nicht zu sagen schizophren), dass in der Quantenoptik das klassische Standardmodell für Intensitätsschwankungen thermischer Strahler auch zur Erklärung von Photonenbunching verwendet wird: Man lässt ein Atom endlos strahlen (was auch klassisch unsinnig ist) und ist zufrieden damit, wenn es wenigstens Phasensprünge macht (die ganz klassische Ursachen haben).
Das kommt vielleicht von dem Dogma, dass man den Übergang eines Atoms nicht wie einen gedämpften klassischen Oszillator behandeln darf (weil ja nach Bohr das Elektron springt). Dem ungeachtet berechnet man aber auch in der Quantenmechanik die natürliche Linienbreite ganz ungeniert aus der Lebensdauer eines Zustands (oder umgekehrt). 

Aber natürlich lässt sich Photonenbunching oder Lichtklumpen auch mit dem klassischen Modell der Strahlungsdämpfung erklären. An die Stelle der mittleren Stoßzeit tritt die mittlere Lebensdauer (die Größenordnungen beider Prozesse überdecken weite Bereiche). 

Wir wagen also einen Modellwechsel ohne die Bohrsche Schere im Kopf: Auch ungestörte Atome strahlen nicht endlos mit Phasensprüngen, sondern gedämpft mit Beginn der Abstrahlung zu einem zufälligen Zeitpunkt. Auch hier sind die Standardmodelle 

a) Lorentzlinie (spontane Emission) 

(1)

b) Gausspaket (Laserpuls) 

(2)

Überlagert man 1000 zufällig verteilte Lorentz-Pakete (im Bild oben links), dann sieht die Zeitreihe für chaotisches Licht (Lorentz ohne Stöße) so aus  

Eine qualitativ gleiche Zeitreihe würde ein Funkeninduktor mit Wackelkontakt liefern ;-)).
Mit Gauß-Paketen (im Bild weiter oben rechts) wird sie etwas glatter und nicht mehr so chaotisch... 

Und man ist glücklich, wenn man aus diesen Zeitreihen wieder das Spektrum rechnerisch destillieren kann (Fourier, Wiener-Khintchine), falls man gerade kein Prisma oder Gitter zur Hand hat.

Und die Lehre von der Geschicht? Rauschen - mit und ohne Klumpen - ist ein ziemlich klassisches Phänomen!