Feynmans Herleitung der Schrödingergleichung
Text auszugsweise aus
Feynman
and Hibbs Quantum Mechanics and Path Integrals,
McGraw-Hill Publishing Company 1965. 4. Kapitel
Formeln (blau): Die "Rechnung" wurde mit Maple symbolisch durchgeführt.
4 The Schrödinger Description of Quantum Mechanics
The path integrals which we have discussed so far have integrands which are exponentials of actions with the property (4-1)
![]()
Such path integrals can be analyzed in terms of the properties of integral equations which can be deduced from them. [...]
A still more convenient method is to reduce the path integrals to differential equations if possible. This possibility exists in quantum mechanics and is, in fact, the most convenient way to present that theory. It is in almost every case easier to solve the differential equation than it is to evaluate the path integral. The conventional presentation of quantum mechanics is based on this equation, called the Schrödinger equation. Here we shall derive this equation from our formulation. [...]
In this chapter our purpose is twofold: (1) For the reader primarily interested in quantum mechanics our aim is to connect the path integral formulation with other formulations which are found in the standard literature [...]. (2) For the reader primarily interested in path integrals this chapter will show a technique which is available for a certain class of path integrals to reduce these path integrals to differential equations. This technique is best shown by the particular example of quantum mechanics which we shall develop here.
THE SCHRÖDINGER EQUATION
The Differential Equation Form. The
reason that we can develop a differential equation is that the
relationship of Eq. (4-1) is correct for any values of the points 1, 2 and
3. For example, the time can be only an infinitesimal time
![]() greater than the time
greater than the time ![]() . This will permit us to relate the value of a path
integral for one time to its value a short time later. In this manner we
can obtain a differential equation for the path integral.
. This will permit us to relate the value of a path
integral for one time to its value a short time later. In this manner we
can obtain a differential equation for the path integral.
We have already found that as a consequence of Eq. (4-1) we can define a wave function. Furthermore, we know that the equation (4-2)
![psi(x[2],t[2]) = Int(K(x[2],t[2],x[1],t[1])*psi(x[1],t[1]),x[1] = -infinity .. infinity)](images/feyschroehtm4.gif)
gives the wave function at a time ![]() in terms of the wave function at a time
in terms of the wave function at a time ![]() . In order to obtain the differential equation we
seek, we apply this relationship in the special case that the time
. In order to obtain the differential equation we
seek, we apply this relationship in the special case that the time
![]() differs only by an infinitesimal interval
differs only by an infinitesimal interval ![]() from
from ![]() . The kernel K(2,1) is proportional to the
exponential of
. The kernel K(2,1) is proportional to the
exponential of
![]() (
(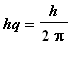 ) times the action for the interval
) times the action for the interval ![]() to
to ![]() . For a short interval
. For a short interval ![]() the action is approximately
the action is approximately ![]() times the lagragian for this interval. That is,
using the same approximation as that of Eq. (2-34)
times the lagragian for this interval. That is,
using the same approximation as that of Eq. (2-34)
![K(i+1,i) = `1/A`*exp(i*epsilon/hq*L((x[i+1]-x[i])/epsilon,1/2*x[i+1]+1/2*x[i],1/2*t[i+1]+1/2*t[i]))](images/feyschroehtm16.gif)
we have (4-3)
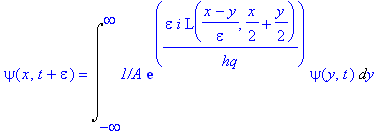
We shall now apply this to the special case of a particle moving in a potential V(x,t) in one dimension, i.e., that for which
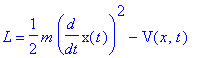
In this case Eq. (4-3) becomes (4-4)
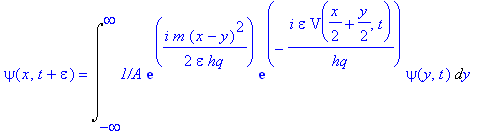
The quantity
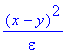
appears in the exponent of the first factor. It is clear that if y is appreciably differentfrom x, this quantity is very large and the exponential consequently oscillates very rapidly as y varies. When this factor oscillates rapidly, the integral over y gives a very small value (because of the smooth behavior of the other factors). Only if y is near x (where the exponential changes more slowly) do we get important contributions. For this reason we make the substitution
![]()
with the expectation that
appreciable contributions to the integral will occur only for small
![]() .
We obtain (4-5)
.
We obtain (4-5)
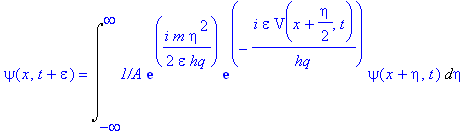
The phase of the first exponential
changes by the order of 1 radian when
![]() is of the order
is of the order
![]()
so that most of the integral is
contributed by values of
![]() in this order.
in this order.
We may expand ![]() in a power series. We need only keep terms of
order
in a power series. We need only keep terms of
order
![]() . This implies keeping second-order terms in
. This implies keeping second-order terms in ![]() . The term
. The term
![]()
may be replaced by
![]()
because the error is of higher order
than
![]() . Expanding the left-hand side to first order in
. Expanding the left-hand side to first order in ![]() and the right-hand side to first
order in
and the right-hand side to first
order in
![]() and second order in
and second order in ![]() , we obtain (4-6)
, we obtain (4-6)
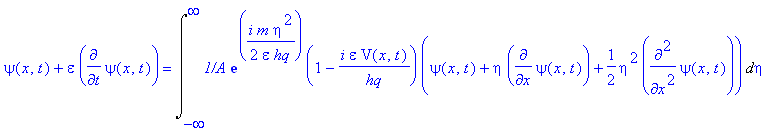
If we take the leading term on the right-hand side, we have the quantity
![]()
multiplied by the integral (4-7)
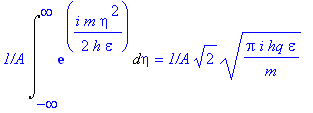
On the left-hand side we just have ![]() . In order that both sides agree in the limit
. In order that both sides agree in the limit ![]() approaches 0, it is necessary that A
be so chosen that the expression of Eq. (4-7) equals 1. That is
(4-8),
approaches 0, it is necessary that A
be so chosen that the expression of Eq. (4-7) equals 1. That is
(4-8),
![]()
[...]. This is a way of obtaining
the quantity
A in more complicated problems also. The A must
be so chosen that the equation is correct to zero order in
![]() . Otherwise, no limit will exist as
. Otherwise, no limit will exist as ![]() approaches 0 in the original path integral.
approaches 0 in the original path integral.
In order to evaluate the right-hand side of Eq. (4-6), we shall have to use two integrals (4-9)
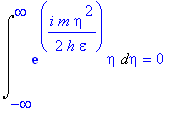
and (4-10)
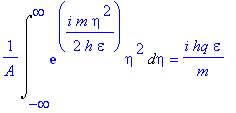
Writing out the right-hand side of Eq. (4-6) gives (4-11)
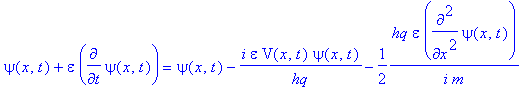
This will be true to order ![]() if
if ![]() satisfies the differential equation (4-12)
satisfies the differential equation (4-12)
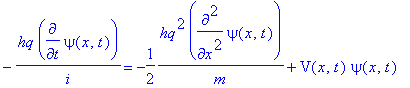
This is the Schrödinger equation for our problem of a particle moving in one dimension. Corresponding equations in more complicated situations can be worked out in the same way.
|
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top |
