Der Doppelspaltversuch wird oft herangezogen, um den Welle-Teilchen-Dualismus oder auch das Komplementaritätsprinzip - also Quantenphänomene - zu erklären, nach dem Motto: "Wenn der Weg des Photons (Elektrons,...) bestimmt wird, oder auch nur bestimmt werden kann, verschwindet die Interferenz". Dass dies nicht unproblematisch ist, und der Doppelspaltversuch und das "komplementäre Verhalten" in den allermeisten Fällen rein klassisch beschrieben werden kann, soll hier gezeigt werden. 

Im Folgenden gilt: Intensität ~ Amplitude². Beide Begriffe werden je nach Kontext verwendet, d.h. Amplitude, wenn man an Welle denkt und Intensität, wenn man an Strahlen denkt. 

Gliederung:

• Sichtbarkeit
• Interferenz zweier Kreiswellen mit Berücksichtigung der Sichtbarkeit
• Doppelspalt endlicher Breite

Sichtbarkeit 

In den gängigen Argumentationen zum Dualismus oder zum Komplementaritätsprinzip (meist Gedankenexperimente) spielt die Sichtbarkeit des Interferenzmusters kaum eine Rolle, bzw. wird als maximal (100%) angenommen. In realen Experimenten spielt sie aber eine zentrale Rolle. 

Die Sichtbarkeit ist so definiert: 

 

Intensität hinter Doppelspalt 

 

und sind die Teilintensitäten von Spalt 1 und 2 und ist der Phasenunterschied der beiden Strahlen im Interferenzpunkt. Für die maximale bzw. minimale Intensität erhält man also 

 

was in die Gleichung für V eingesetzt ergibt: 

 

und sich leicht merken lässt als Quotient des geometrischen und des arithmetischen Mittels der Intensitäten. Da man meistens = voraussetzt, ist dann (). Für unterschiedliche Intensitäten (oder Amplituden) trifft das aber nicht mehr zu.  

Zunächst eine 3D-Darstellung für den Überblick 

 

Die Sichtbarkeit V (nach oben abgetragen) hat zwar ein "breites Maximum" über der Winkelhalbierenden, aber die Argumentation "V ist so gut wie überall gleich 1" ist die entscheidende Fehlerquelle für oben genannte Gedankenexperimente und ähnliche "Idealisierungen". 

Aber zunächst ein paar weitere Formulierungen für und Veranschaulichungen von V. 

Mit der gesamten Intensität   erhält man V =

 

oder V =  

 

Auf 1 normiert (Gesamtintensität=1 und =x) 

 

 

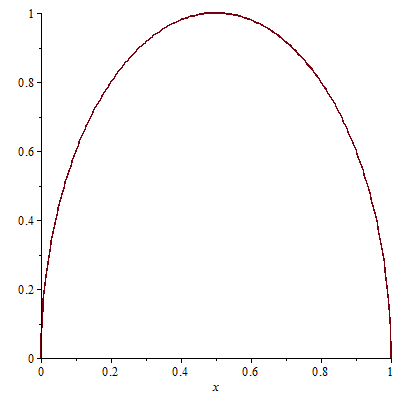
Das ist ein in Richtung V um den Faktor 2 gedehnter Halbkreis und bedeutet umgekehrt, dass das Maximum von V nicht nur "breit ist", sondern dass die Sichtbarkeit an den Intervallenden (unendlich) steil ansteigt: Schon bei einem Verhältnis der Intensitäten von nur 1% hat man 20% Sichtbarkeit. 

Verwendet man das Verhältnis v der Intensitäten 

so ergibt sich eine weitere Art der Darstellung

 

Bzw. mit dem Verhältnis (wieder v) der Amplituden 

 

Nach diesen Vorüberlegungen können wir die Sichtbarkeit des Interferenzmusters beim Doppelspaltversuch untersuchen. Der Fall gleicher Intensitäten ist völlig uninteressant (V = 1). Unterschiedliche aber konstante Intensitäten sind auch nicht viel interessanter, weil sie eine konstante Sichtbarkeit liefern. 

Wirklich interessant ist nur das Realexperiment, in dem die Amplituden (der Wellen aus einer Öffnung) nicht nur unterschiedlich sondern auch ortsabhängig sein können, z.B. und (ra, rb = Abstände der Öffnungen vom Interferenzpunkt), wenn man Kugelwellen statt der "idealisierten" ebenen Wellen mit konstanter Amplitude nimmt. 

Damit ergibt sich: 

oder

 

Für die Sichtbarkeit Vr in der x-y-Ebene hinter den zwei Öffnungen bei +-xa. Wenn wir zunächst "zwei gleiche Öffnungen" (a = b) annehmen, sieht das so aus: 

 

Was die gängige Idealisierung zu bestätigen scheint: schon bei geringem Abstand zum Doppelspalt beginnt die "Fernzone" und die Interferenz wird voll sichtbar (weiße Fläche ohne Höhenlinien). Nur in der "Nahzone" kann Interferenz nicht beobachtet werden (schwarze Bereiche bei x = +-2). Wobei dieses Ergebnis (Übergang von der Nah- in die Fernzone) überhaupt nicht von der Wellenlänge abhängt, sondern nur vom Abstand der Öffnungen, d.h. der Geometrie der Anordnung: Strahlenoptik oder Wellenoptik? 

3D-Darstellung 

 

Was passiert für unterschiedliche Öffnungen, z.B. Faktor 4 für die Amplituden (Faktor 16 für die Intensitäten)? 

 

Bei der Öffnung mit großer Intensität (links) verschwindet die Sichtbarkeit der Interferenz: Teilchen. Bei der Öffnung mit kleiner Intensität ist sie am höchsten: Welle! Dualismus? 

Das Ganze noch einmal in 3D und Farbe: 

 

In diesem Beispiel ist die Sichtbarkeit in der "Fernzone" konstant etwa gleich 50%.   

 

Und was hat das Ganze mit Komplementarität zu tun? 

Wenn man die Wege eines Photons am Doppelspalt bestimmen will (unterscheidbar machen will), muss man das in der Nahzone (direkt hinter einer Öffnung) tun: "Ortsmessung"! Das Interferenzmuster beobachtet man in der Regel in der Fernzone (= Richtungs- oder "Impulsmessung"). Alles ganz klassisch (bis auf das Photon)! Aber nicht komplementär im Sinne von entweder oder: Das Interferenzmuster verschwindet nämlich nie komplett (in der Fernzone sind die Amplituden "praktisch gleich"). 

Und es gibt noch ein weiteres Problem. Wenn man etwa hinter einem Spalt einen Detektor (oder ein Hindernis) für die Ortsmessung aufstellt, bedeutet das für die Fernzone, dass das dort registrierte Photon durch den anderen Spalt kam, was die Sichtbarkeit der Interferenz in der Fernzone verringert. Aber - oh Wunder - dafür wird die Sichtbarkeit der Interferenz in der Nahzone maximal! 

Das liegt natürlich daran, dass das Photon immer in einer Mode steckt, die mit klassischen Formeln beschrieben werden kann. 

Wir sollten die etwas pauschalen Überlegungen zur Sichtbarkeit, also zum Unterschied der Interferenzmaxima und -minima durch das Interferenzmuster ergänzen:

 

Interferenz zweier Kreiswellen mit Berücksichtigung der Sichtbarkeit 

Im Folgenden werden punktförmige Öffnungen (Quellen) angenommen, die aber unterschiedliche Intensität haben können.  

 

Abstand zu Punktquellen (nur in der x-z-Ebene) 

 

 

Intensität 

 

wobei mit die Polarisation berücksichtigt werden kann, was aber nur einen konstanten Faktor (0..1) liefert. Mit dem Phasenunterschied   

 

erhält man für die Intensität 

 

 

Konstante Amplitude (hinter dem Doppelspalt). Wellenlänge = 1 [ Anmerkung], Öffnungen bei x = +-2, zusätzlich sind Höhenlinien der Intensität eingezeichnet.

 

Das Interferenzmuster (in einer Ebene senkrecht zum Doppelspalt) ändert natürlich nicht seine Form. Nur die Sichtbarkeit ändert sich - egal ob wegen unterschiedlicher Amplitude oder wegen Polarisation! In der Draufsicht sieht man immer nur die bekannten 'Interferenzhyperbeln', die Maxima sind weiß und bei 100% Sichtbarkeit wären die Minima in diese Darstellungsart schwarz (und nicht nur grau).

 

Ortsabhängige Amplitude 

 

Gleiche Amplitude an den Öffnungen 

So sieht also ein realistisches Interferenzmuster aus: In der "Nahzone" verschwinden die Minima, weil durch die 1/r-Abhängigkeit der Unterschied in den Amplituden zu groß wird (außer in der Mitte). Man sollte eben 1/r-Quellen nicht zu nahe kommen...

Unterschiedliche Amplitude an den Öffnungen (wie oben A2 = 4*A1) 

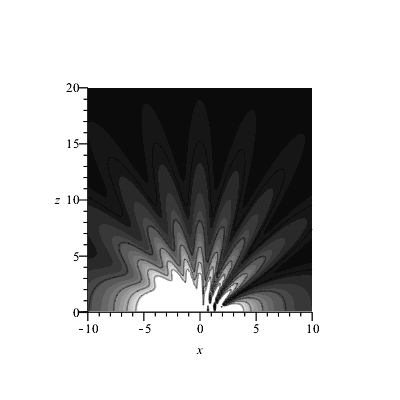
In der Fernzone ist die Interferenz immer zu sehen - mit fast konstanter Sichtbarkeit (s.o.). 

Interpretation à la Kopenhagen: Große Intensität für eine (punktförmige) Öffnung bedeutet, dass das Photon mit großer Wahrscheinlichkeit diese Öffnung passiert hat - in der Nahzone. Kleine Amplitude für die andere Öffnung kann aber für die Fernzone bedeuten, dass man vor dieser Öffnung einen Detektor (oder nur ein Hindernis oder nur ein Atom) aufgestellt hat, mit dem der Ort bestimmt werden kann. Dann müsste doch die Interferenz komplett verschwinden? Gehirnwäsche! 

 

Schnitte für z = const (nah und fern), also Intensitätsverteilung auf dem Schirm: 

 

Polarisation 

Selbst wenn man zusätzlich zu den verschiedenen Intensitäten (der beiden Quellen) die Polarisation fast orthogonal wählt (80°), verschwindet die Interferenz nicht komplett: 

 

 

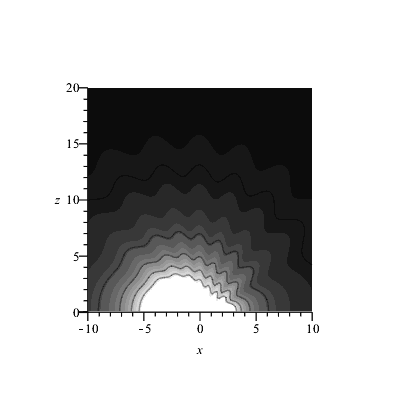
Das Photon steckt immer in einer klassischen Mode - auch das polarisierte! 

 

Doppelspalt endlicher Breite 

Idealisierungen sind meist Euphemismen - nicht nur in der Physik. Allen voran die 'punktförmige Quelle'. Wenn es zu kompliziert wird, einen Sachverhalt realistisch zu beschreiben, reduziert man ihn auf einen Punkt und nennt die gröbste aller Näherungen ("in nullter Ordnung ist die Erde ein Ziegelstein") ideal. 

Im Folgenden wird eine Öffnung endlicher Breite als eine Reihe dicht liegender Elementarzentren (oder idealer Zentren?) modelliert (Huygens). "Dicht" bedeutet: der Abstand der Zentren ist sehr klein gegen die Wellenlänge der Strahlung.  

Die "Idealisierung" Elementarzentrum ist hier also nur eine Rechenhilfe, weil es ideal "geschlossene/analytische Lösungen" nicht gibt und numerische Integrationen Rechenzeit verschlingen. Das ist aber ein probates Mittel, die Realität zu approximieren und man kann damit auch bequem den Welle-Teilchen-Dualismus modellieren: 

Welle (Quadrat der Summe der Amplituden) 

konstante Amplitude, gleiche Öffnungen 

 

Die Öffnungen liegen nun bei x = +-10. Im Gegensatz zu punktförmigen Öffnungen gibt es nun erst in der Fernzone deutliche Maxima (weiß). Warum wohl?

Konstante Amplitude, unterschiedliche Öffnungen: 

 

Die linke Öffnung (bei x = -10) besteht aus 61 Elementarzentren (äquidistant wie oben), die rechte (bei x = 10, ja dort liegt sie wirklich!) aus einem einzigen. Selbst in gröbster Näherung (konstante Amplitude) ist also Interferenz hinter dem fast geschlossenen Spalt zu sehen - und zwar in der Nahzone! Woran liegt das wohl?

Amplitude ~ 1/r, gleiche Öffnungen 

 

Animation mit zunehmender Spaltbreite (rechts)  

 

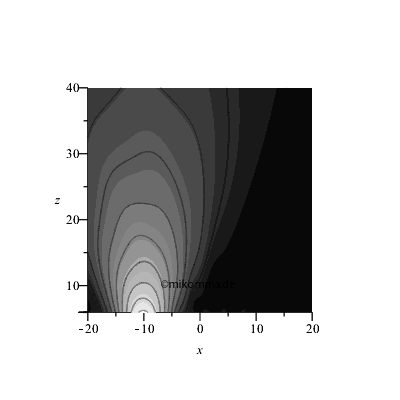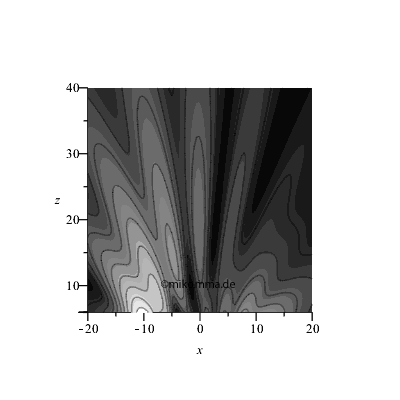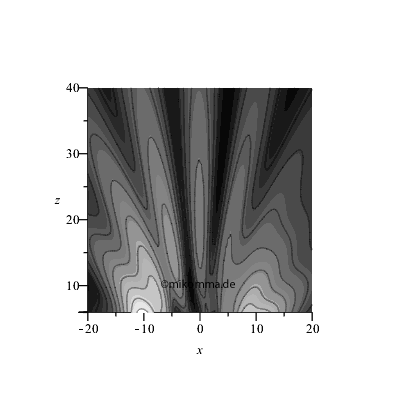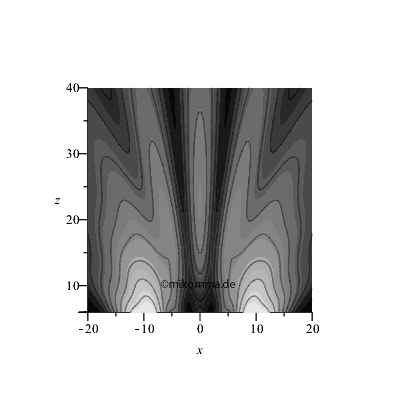
Es genügt schon ein einziges Elementarzentrum im zweiten Spalt (bei x = 10), um die "Nichtinterferenz zu stören"! 

 

Teilchen (Summe der Quadrate). Ortsunabhängige Sichtbarkeit ist wieder uninteressant, weil konstant. 

Intensität = Teilchenzahldichte ~ 1/r^2 (die z-Achse beginnt bei 6) 

Gleiche Öffnungen

Unterschiedliche Öffnungen: links 61 Zentren, rechts 21:

 

Teilchen sind eben nicht sehr interessant - gibt es sie überhaupt?

Zum Schluss noch die oft gesehenen und bei Abituraufgaben sehr beliebten Skizzen zum Dualismus mit obigem Modell (und obigen Daten) erstellt:

Teilchenverteilung auf einem Schirm bei z = 2 (unterschiedliche Öffnungen)

 

Die 1/r^2-Abhängigkeit liefert 'automatisch' zwei Maxima in der Nahzone, es muss also keine Wechselwirkung der "Teilchen" mit den Rändern der Öffnungen o.ä. eingeführt werden.

In den folgenden Animationen wird der Schirm von der Nah- und Fernzone geschoben. Links Teilchen, rechts Welle.

 

Ungleiche Öffnungen

Gleiche Öffnungen (Intensität logarithmisch)

Es gibt übrigens einen einfachen Freihandversuch zu diesem Thema, der sich mit den Mitteln einer Standard-Physik-Sammlung durchführen lässt:

Man beleuchtet einen Doppelspalt mit mit einem (aufgeweiteten) Laserstrahl und betrachtet das Interferenzmuster in großer Entfernung auf einem Schirm. Deckt man mit einem Blatt Papier einen der beiden Spalte schräg ab, so ändert sich die Sichtbarkeit des Interferenzmusters von 0 (Einfachspalt) zu 1 (zwei Spalte gleicher Breite). Dieser "Dualismus" lässt sich auch rechnerisch leicht modellieren:

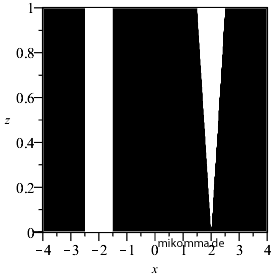Das linke Bild zeigt die Durchlassfunktion eines "V-förmigen Doppelspalts" (weiß = 1, schwarz = 0). Das V ist hier symmetrisch zur Vertikalen, was sich mit einem Blatt Papier natürlich nicht erreichen lässt, aber V steht hier nur für Visibility. Das mittlere und das rechte Bild zeigen das Betragsquadrat der Fouriertransformierten der Durchlassfunktion. Beliebige Einheiten in allen Darstellungen, k ist die Wellenzahl parallel zum Schirm (oder der Querimpuls des Photons).
Natürlich kann man das Experiment auch mit einzelnen Photonen machen. Am unteren Rand (z= 0) verhält sich also das Photon wie ein Teilchen, das durch den linken Spalt geht? Nein: wie eine Welle, die am linken Spalt gebeugt wird! Man kennt also nur den Ort des Photons (bis auf die Spaltbreite), aber nicht den Weg, den es danach nimmt.
Am oberen Rand (z = 1) verhält sich das Photon wie eine Welle, die an zwei Spalten gleicher Breite gebeugt wird (es gibt mit Sicherheit keine Welcher-Weg-Information für ein fiktives Teilchen).
Aber besonders spannend ist natürlich die Frage, wie es ein (einziges) Photon schafft, am unteren Rand (annähernd) Teilcheneigenschaften zu zeigen, und am oberen Rand ein Interferenzmuster mit voller Sichtbarkeit zu erzeugen (das können wirklich nur Wellen :-)). Und dann gibt es in dieser Anordnung ja noch alle Werte für V zwischen 0 und 1 ...

Hier ist noch eine Variante:


Das kann alles eigentlich nur funktionieren, wenn sich das Photon nicht um die verkorkste Logik (oder den quantentheoretischen Überbau?) von Welcher-Weg-Experimenten (dieser Art!) kümmert, ganz zu schweigen von den Überlegungen zur Retrokausalität, die in "Wissenschafts"-Journalen immer wieder gerne ausgepackt werden, um dem Leser das Fürchten zu lehren!

Apropos Retrokausalität oder "delayed choice": Auch hierzu gibt es ein einfaches Experiment. Man bildet auf dem Schirm nicht das Interferenzmuster ab, sondern den Doppelspalt, was sich mit einer Linse (frei Hand) leicht bewerkstelligen lässt. Wenn man den Doppelspalt auf dem Schirm sieht, interferiert das Photon nicht mit sich selbst, man kennt also im Prinzip seinen Weg (welchen nun?). Bringt man die Linse erst in den Strahlengang (?!), nachdem das Photon den Doppelspalt passiert hat, so "zwingt man das Photon" rückwirkend, "seinen Teilchencharakter zu offenbaren". Dieses Experiment lässt sich übrigens auch so durchführen, dass man hinter dem Doppelspalt einen Strahlteiler verwendet, der das Photon auf einem Ausgang (oder Weg?) durch die Linse schickt und auf dem anderen Ausgang direkt zum Interferenzmuster. So einfach ist Physik!

Interferenz - quantenoptisch | Quantenradierer | Photon am Doppelspalt | Gitter | Punktgitter | Kreuzgitter | Raumgitter | Beugung | Fresnelbeugung | Zeiger | Interferenz

Moderne Physik mit Maple

HOME | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Mathematik | Top