

Interferenz - quantenoptisch
Auszug aus einem Maple-Worksheet, in Anlehnung an L. Mandel, Quantum effects in one-photon and two-photon interference, Reviews of Modern Physics, Vol. 71, No. 2, Centenary 1999.
Anmerkungen zu Maple 2018: Das Physics-Package (Maplesoft) erlaubt das Rechnen mit Kets und Bras, ist aber noch verbesserungsfähig, insbes. was das Rechnen in Produkträumen angeht. Der Export von Worksheets nach HTML hat bei Maplesoft nicht die oberste Priorität (in der Nachbearbeitung des Layouts dieses Artikels steckt mehr Arbeit als "in der Physik" :-).
In der Quantenoptik beschreibt man Interferenz durch die Überlagerung von Moden, in denen sich Photonen befinden. Mit einer Mode ist dabei die elektrische Feldstärke als Funktion von Ort und Zeit gemeint (meistens eine ebene Welle -> Anmerkung) und das Photon wird (mathematisch) durch Operatoren erzeugt, bzw. vernichtet. Die Messgröße ist wie in der klassischen Physik die Intensität, also das Betragsquadrat der elektrischen Feldstärke, bzw. der Erwartungswert davon.
Zur Orientierung zunächst eine Prinzipskizze:
 |
Zum
Vergleich die Skizze aus dem Original: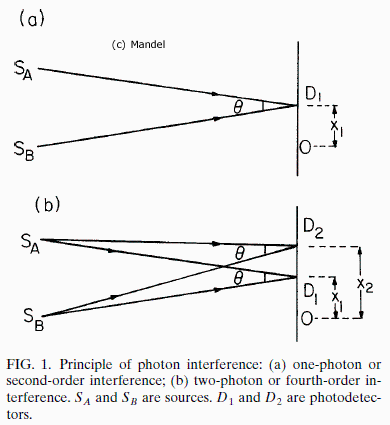 |
In den Quellen A und B werden Photonen erzeugt und in ![]() bzw.
bzw. ![]() nachgewiesen ("vernichtet"). Verwendet man nur einen Detektor (z.B in
nachgewiesen ("vernichtet"). Verwendet man nur einen Detektor (z.B in ![]() ), so spricht man von "Amplitudeninterferenz" oder mit Mandel von "Interferenz 2. Ordnung" (2. Ordnung, weil das Quadrat der E-Feldstärke gemessen wird) - also von der "ganz normalen Interferenz". Misst man mit zwei Detektoren (in
), so spricht man von "Amplitudeninterferenz" oder mit Mandel von "Interferenz 2. Ordnung" (2. Ordnung, weil das Quadrat der E-Feldstärke gemessen wird) - also von der "ganz normalen Interferenz". Misst man mit zwei Detektoren (in ![]() und
und ![]() ) in Koinzidenz, so spricht man von "Intensitätskorrelation" oder mit Mandel von "Interferenz 4. Ordnung"
(die Messgröße ist das Produkt der Intensitäten). In jedem Fall bestimmen die Phasen Φ (bzw. die optischen Weglängen) das Interferenzmuster.
Neben der von Mandel verwendeten Ordnung ist auch Interferenz 1. Ordnung
(Amplitude) und Interferenz 2. Ordnung (Intensität) gebräuchlich. Wichtiger: Ob Interferenz beobachtbar ist, hängt von der Art der Quellen ab: A und B können primäre Quellen sein (z.B. Atome oder Laserstrahlen), oder sekundäre Quellen (z.B. Doppelspalt oder Strahlteiler), die von einer primären Quelle Q beleuchtet werden.
) in Koinzidenz, so spricht man von "Intensitätskorrelation" oder mit Mandel von "Interferenz 4. Ordnung"
(die Messgröße ist das Produkt der Intensitäten). In jedem Fall bestimmen die Phasen Φ (bzw. die optischen Weglängen) das Interferenzmuster.
Neben der von Mandel verwendeten Ordnung ist auch Interferenz 1. Ordnung
(Amplitude) und Interferenz 2. Ordnung (Intensität) gebräuchlich. Wichtiger: Ob Interferenz beobachtbar ist, hängt von der Art der Quellen ab: A und B können primäre Quellen sein (z.B. Atome oder Laserstrahlen), oder sekundäre Quellen (z.B. Doppelspalt oder Strahlteiler), die von einer primären Quelle Q beleuchtet werden.
Im ersten Fall ist ![]() ein Produktzustand, im zweiten Fall wird aus
ein Produktzustand, im zweiten Fall wird aus ![]() ein Superpositionszustand
- mehr oder weniger kohärent bzw. verschränkt, und im Folgenden meist als "Doppelspalt"
apostrophiert.
ein Superpositionszustand
- mehr oder weniger kohärent bzw. verschränkt, und im Folgenden meist als "Doppelspalt"
apostrophiert.
Darüber hinaus spielt die Art des verwendeten Lichts eine wichtige Rolle. Die zwei wichtigsten Lichtsorten sind
a) Nummerzustände (Fockzustände) und
b) kohärente Zustände (Glauberzustände).
Mit "Interferenz von Photonen" ist immer die Interferenz von Photonen in der gleichen Mode (Wellenlänge, Polarisation,...) gemeint.
Wir stellen zunächst die benötigten Operatoren und Zustände zusammen:
a) Fock
Vernichtungsoperatoren
| > | ama:=Annihilation(A,1,explicit) |
|
|
(1) |
| > | amb:=Annihilation(B,1,explicit) |
|
|
(2) |
und Erzeugungsoperatoren
| > | cma:=ama^*; cmb:=amb^*; |
|
|
|
|
|
(3) |
Zustände
| > | KA:=Ket(A,n); KB:=Ket(B,m); |
|
|
|
|
|
(4) |
Abkürzung für den Zustand nach A und B
| > | KAB:=Ket(Psi,AB) |
|
|
(5) |
Also z.B.
| > | KAB=KA*KB |
|
|
(6) |
Wirkung der Operatoren testen:
| > | cma.ama.amb.KA.KB |
|
|
(7) |
oder z.B.
| > | (%Bracket=Bracket)(KA^*,cma.ama,KA*KB) |
|
|
(8) |
(Die linke Seite wird z.Zt. (Maple 2018) mit einem Ket zu viel geschrieben.)
Doppelspalt
Transformation des Zustands am Doppelspalt, der mit n Photonen beleuchtet wird:
| > | DS:=n->1/sqrt(n!)*(1/sqrt(2))^n*(cma+cmb)^n.(Ket(A,0)*Ket(B,0)) |
 |
(9) |
| > | DS(n) |
 |
(10) |
D.h., "Photonen werden am Doppelspalt binomial verteilt", z.B.:
| > | KAB=DS(5) |
|
|
(11) |
Auf Anregung des Autors dieses Artikels wurde Anfang 2018 im Physics-Package die Option "hideketlabel" als Workaround eingeführt, mit der sich die übliche Kurzschreibweise realisieren lässt. Dann lautet der Zustand für
Ein Photon
| > | KAB=DS(1) |
|
|
(12) |
Zwei Photonen
| > | KAB=DS(2) |
|
|
(13) |
(Anm.: |1>|1> beschreibt ein "Biphoton" (zwei Photonen in zwei Moden), im Ggs. zum Zustand |2>, also zwei Photonen in einer Mode.)
Fünf Photonen
| > | KAB=DS(5) |
|
|
(14) |
b) Glauber
| > | KAc:=Ket(ama,alpha); KBc:=Ket(amb,beta); |
|
|
|
|
|
(15) |
Test:
| > | KAc^* .ama^* ,KBc^* .amb^* |
|
|
(16) |
Nicht gerade die übersichtlichste Notation...
Doppelspalt
| > | KA2c:=Ket(ama,alpha/sqrt(2)) |
 |
(17) |
| > | ama.KA2c |
 |
(18) |
oder mit "versteckten Labeln":
| > | ama.KA2c |
 |
(19) |
Wie bei klassischem Licht wird die Intensität halbiert (bei gleichen Amplituden am Doppelspalt).
Mit diesen Operatoren und Zuständen können wir folgende Erwartungswerte berechnen (Kopien aus dem Original):


Im Vergleich zu Mandels Artikel lassen wir im Folgenden die Ansprechwahrscheinlichkeiten![]() und
und![]() der Detektoren weg, bzw. setzen sie gleich 1.
der Detektoren weg, bzw. setzen sie gleich 1.
Der Operator E(+) für das elektrische Feld (positiver Frequenzanteil) lautet dann:
| > | E:=i->fa[i]*ama+fb[i]*amb |
|
|
(20) |
also z.B.
| > | 'E(x[1])'=E(1) |
|
|
(21) |
mit den komplexen Amplituden ![]() und
und![]() (sinngemäß für
(sinngemäß für ![]() ).
).
Nach diesen Vorbereitungen nun zur Interferenz zweiter Ordnung:
Interferenz 2. Ordnung
a) Fock
Der Operator für das Quadrat der Feldstärke lautet
| > | P1:=E(1)^* . E(1) |
|
|
(22) |
1. Unabhängige Quellen
Der Produktzustand mit n Photonen in der Mode A und m Photonen in der Mode B
| > | KAB=KA.KB |
|
|
(23) |
hat dann den Erwartungswert
| > | (%Bracket=Bracket)(Dagger(KA.KB),P1,KA.KB) |
|
|
(24) |
| > | EW1:=Dagger(KA.KB).P1.KA.KB |
|
|
(25) |
D.h., man sieht keine Interferenz. Photonen in Nummerzuständen aus verschiedenen unabhängigen Quellen interferieren nicht, benehmen sich also wie klassisches inkohärentes Licht. Oder wie schon P.A.M. Dirac sagte: "Each photon then interferes only with itself. Interference between two different photons never occurs." (The Principles of Quantum Mechanics, 1957, S. 9)
2. Doppelspalt
Ein Photon aus Q (gleicher Abstand zu A und B) wird zu:
| > | KAB=DS(1) |
 |
(26) |
mit dem Erwartungswert in x1:
| > | DS1:=Dagger(DS(1)).P1.DS(1) |
![Typesetting:-mprintslash([DS1 := `+`(`*`(`/`(1, 2), `*`(conjugate(fa[1]), `*`(fb[1]))), `*`(`/`(1, 2), `*`(`^`(abs(fa[1]), 2))), `*`(`/`(1, 2), `*`(`^`(abs(fb[1]), 2))), `*`(`/`(1, 2), `*`(conjugate(f...](qoim/interqo_46.gif) |
(27) |
Nun sieht man Interferenzterme (die gemischten Terme)
Wir schreiben die komplexen Amplituden in polarer Notation (Betrag und Phase):
| > | fas:=seq(fa[i]=f[A]*exp(I*phi[A||i]),i=1..2); fbs:=seq(fb[i]=f[B]*exp(I*phi[B||i]),i=1..2) |
|
|
|
|
|
(28) |
Und erhalten für die Intensität
| > | IDS1:=combine(evalc(subs(fas,fbs,DS1))) |
|
|
(29) |

Also das bekannte Interferenzmuster für gleiche Amplituden (= 1 im Bild).
Die Sichtbarkeit als Animation:
| > | eval(IDS1,[phi[B1]=0,f[A]=1]) |
|
|
(30) |
 |
Für 5 Photonen aus Q erhalten wir
| > | DS5:=Dagger(DS(5)).P1.DS(5) |
![Typesetting:-mprintslash([DS5 := `+`(`*`(`/`(5, 2), `*`(`^`(abs(fa[1]), 2))), `*`(`/`(5, 2), `*`(`^`(abs(fb[1]), 2))), `*`(`/`(5, 2), `*`(conjugate(fa[1]), `*`(fb[1]))), `*`(`/`(5, 2), `*`(conjugate(f...](qoim/interqo_55.gif) |
(31) |
oder
| > | combine(evalc(subs(fas,fbs,DS5))) |
|
|
(32) |
Und es dürfte nicht schwer zu erraten sein, dass wir auch mit n Photonen das klassische Ergebnis erhalten. Warum? "Weil am Doppelspalt jedes Photon mit sich selbst interferiert!" (frei nach Dirac, s.o.). Das liegt daran, dass sich jedes Photon hinter dem Doppelspalt in einem Überlagerungszustand (oder sogar verschränkten Zustand - mit anderen Photonen und sich selbst) befindet.
b) Glauber
1. Unabhängige Quellen, z.B. zwei Laser "in der gleichen Mode":
Die Rechnung für kohärente Zustände lässt sich abkürzen, indem man die Operatoren durch ihre Eigenwerte ersetzt (im aktuellen Zustand (Juli 2018) des Physics-Package kann sie nicht mit dem Physics-Package durchgeführt werden):
| > | EW1c:=(subs(ama=alpha,amb=beta,ama^* =conjugate(alpha),amb^* =conjugate(beta),P1)) |
|
|
(33) |
| > | EW1c:=simplify(%) |
|
|
(34) |
Übergang zur polaren Notation
| > | EW1c:=combine(evalc(subs(fas,fbs,EW1c))) |
|
|
(36) |
(Ja, das ist z.Zt. alles noch etwas umständlich... :-)
Eigenwerte mit Betrag und Phase
| > | subs(alpha=abs(alpha)*exp(I*pa),beta=abs(beta)*exp(I*pb),EW1c) |
|
|
(37) |
| > | evalc(%) |
|
|
(38) |
| > | Intensc:=combine(%) |
|
|
(39) |
Mit dem Phasenunterschied
δ der Zustände
(![]() und
und ![]() sind die mittleren Photonenzahlen) erhält man:
sind die mittleren Photonenzahlen) erhält man:
| > | Intenscd := abs(alpha)^2*(f[A]^2)+abs(beta)^2*(f[B]^2)+2*abs(alpha*beta)*f[A]*f[B]*cos(phi[A1]-phi[B1]+delta) |
|
|
(40) |
Na endlich:
Photonen aus verschiedenen Quellen in kohärenten Zuständen interferieren ganz klassisch! Allerdings handelt es sich hier um Momentanwerte, d.h., die Amplituden (α und β) und insbes. die Phasendifferenz δ sind Funktionen der Zeit und das Interferenzmuster ist nur gut sichtbar, wenn die Laser stabil arbeiten (wie bei klassischen Quellen auch).
Zum Vergleich noch einmal das "klassische Ergebnis":
|
|
(42) |
Also lag Dirac falsch mit seinem Statement "Interference between two different photons never occurs"? Nein, Dirac sagte:
"Some time before the discovery of quantum mechanics people realized that the connexion between light waves and photons must be of a statistical character. What they did not clearly realize, however, was that the wave function gives information about the probability of _one_ photon being in a particular place and not the probable number of photons in that place. The importance of the distinction can be made clear in the following way. Suppose we have a beam of light consisting of a large number of photons split up into two components of equal intensity. On the assumption that the intensity of a beam is connected with the probable number of photons in it, we should have half the total number of photons going into each component. If the two components are now made to interfere, we should require a photon in one component to be able to interfere with one in the other. Sometimes these two photons would have to annihilate one another and other times they would have to produce four photons. This would contradict the conservation of energy. The new theory, which connects the wave function with the probabilities for one photon, gets over the difficulty by making each photon go partly into each of the two components. Each photon then interferes only with itself. Interference between two different photons never occurs."
2. Doppelspalt
Der Doppelspalt kann als kohärente Quelle im Produktzustand
| > | KAB=KA2c*KA2c |
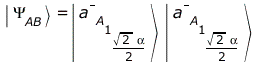 |
(43) |
Kurznotation:
| > | KAB=KA2c*KA2c |
|
|
(44) |
behandelt werden. Man erhält für die Intensität
| > | subs(alpha=alpha/sqrt(2),beta=alpha/sqrt(2),pa=0,pb=0,Intensc) |
![`+`(`*`(`^`(abs(`+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2)), `*`(alpha))))), 2), `*`(`^`(f[A], 2))), `*`(`^`(abs(`+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2)), `*`(alpha))))), 2), `*`(`^`(f[B], 2))), `*`(2, `...](qoim/interqo_77.gif) |
(45) |
oder
| > | simplify(%) |
![`+`(`*`(`/`(1, 2), `*`(`^`(abs(alpha), 2), `*`(`+`(`*`(2, `*`(f[A], `*`(f[B], `*`(cos(`+`(phi[A1], `-`(phi[B1]))))))), `*`(`^`(f[A], 2)), `*`(`^`(f[B], 2)))))))](qoim/interqo_78.gif) |
(46) |
Richtig: Beleuchtet man einen Doppelspalt mit Licht im kohärenten Zustand ![]() , so sieht man
"klassische Interferenz" :-).
, so sieht man
"klassische Interferenz" :-).
Zusammenfassung
a) Fock
Unabhängige (primäre) Quellen: Photonen in Fockzuständen interferieren nicht.
Sekundäre Quellen (Doppelspalt, Strahlteiler,...): Photonen aus Fockzuständen (aus einer Quelle) können interferieren (mit sich selbst).
b) Glauber
Unabhängige (primäre) Quellen: Photonen in Glauberzuständen können interferieren (auch über längere Zeit, wenn man die Quellen stabil hält).
Doppelspalt: Photonen aus Glauberzuständen interferieren - quasi klassisch.
Die zugehörigen Gleichungen lauten:

Interferenz 4. Ordnung
Zur Orientierung der Erwartungswert aus Mandels Artikel:

Der Operator lautet mit unseren Definitionen von oben:
| > | P2 := subsindets(E(1)^* . E(2)^* . E(2) . E(1), specfunc(conjugate), expand) |
|
|
(47) |
a) Fock
1. n Photonen in der Mode A, m Photonen in der Mode B
Erwartungswert der Koinzidenzzählrate in ![]() und
und ![]() für den Produktzustand
für den Produktzustand
| > | KAB=KA*KB |
|
|
(48) |
| > | EW2:=Dagger(KA.KB).P2.KA.KB |
|
|
(49) |
Mit der gleichen Prozedur wie oben (Interferenz 2. Ordnung) erhalten wir (gekürzte Fassung):
Amplituden f mit Betrag und Phase
| > | EW2 := 2*m*n*(f[A]^2)*(f[B]^2)*cos(-phi[A2]-phi[B1]+phi[B2]+phi[A1])+2*m*n*(f[A]^2)*(f[B]^2)+n^2*(f[A]^4)-n*(f[A]^4)+m^2*(f[B]^4)-m*(f[B]^4) |
|
|
(50) |
Die Photonenzahlen m und n entsprechen den Amplitudenquadraten f2. Wir untersuchen die Sichtbarkeit der Interferenz 4. Ordnung am Beispiel des Zustands |1>|1>
2. Jeweils ein Photon in A und B
Mandels Gleichung (5) ergibt mit dem Zustand
| > | Ket(Psi, AB) = Ket(A, 1)*Ket(B, 1) |
|
|
(51) |
die Koinzidenzzählrate
| > | Intens2:=subs(n=1,m=1,EW2) |
|
|
(52) |
Und das ist nicht die klassische Interferenzformel (egal welcher Ordnung)! Hier ein animiertes Beispiel zur Sichtbarkeit:
| > | I2ani:=subs(phi[A2]=0,phi[B2]=0,phi[B1]=0,f[A]=1,Intens2) |
|
|
(53) |
 |
Das ist ein "echter Quanteneffekt": Die Minima der Interferenz 4. Ordnung liegen immer bei 0, bzw. die Sichtbarkeit der Interferenz 4. Ordnung ist immer 100% (im Gegensatz zur Sichtbarkeit der Interferenz 2. Ordnung), vor allem aber im Gegensatz zur Intensitätskorrelation von klassischem Licht (s.u.).
3. Doppelspalt
Superpositionszustände von Fockzuständen unterscheiden sich bei Koinzidenzmessungen nicht wesentlich von Glauberzuständen. Deshalb hier nur ein Beispiel für den Fall, dass "ein Doppelspalt mit 5 Photonen beleuchtet wird". Produkt der Intensitäten:
![]()
Zum Vergleich mit Gleichung (57) unten. Bei der Beleuchtung mit einem Photon ist die Koinzidenzzählrate natürlich Null :).
b) Glauber
1. Momentanwerte
Wir berechnen den Erwartungswert der Koinzidenzzählrate für den Zustand
| > | KAB=KAc*KBc |
|
|
(54) |
Der Operator P2 von oben lautet mit den Eigenwerten α und β:
| > | EW2c:=subs(ama=alpha,amb=beta,ama^* =conjugate(alpha),amb^* =conjugate(beta),P2) |
|
|
(55) |
Mit der Phasenverschiebung δ der kohärenten Zustände ergibt sich für den Erwartungswert nach einer Reihe von Umformungen (zu denen man Maple überreden muss):
|
|
(56) |
In diesem Term (X) bestimmen die Amplituden f,|α| und |β| die Sichtbarkeit. Die Phasen ΦA2 und ΦB2 bestimmen die Amplitude und ΦB1 die Verschiebung und die Phase δ die Amplitude und Verschiebung. Wir wollen hier nur kurz andeuten, wie sich eine Phasenverschiebung zweier "identischer Laser" auf das beobachtete Interferenzmuster (4. Ordnung) auswirkt:
| > | I4c:=simplify(subs(alpha=1,beta=1,X)) |
|
|
(57) |
Animation mit δ:
| > | I4cani:=subs(f[A]=1, f[B]=1, phi[B1]=0,phi[B2]=0, phi[A2]=0,X) |
|
|
(58) |
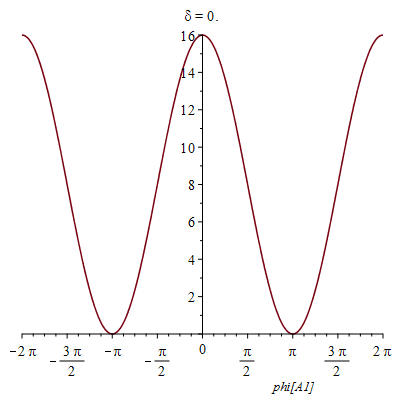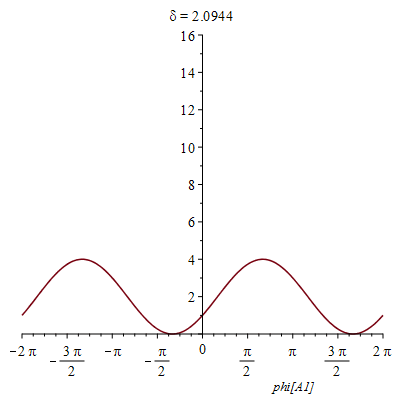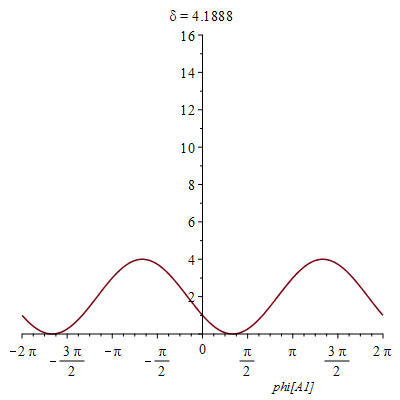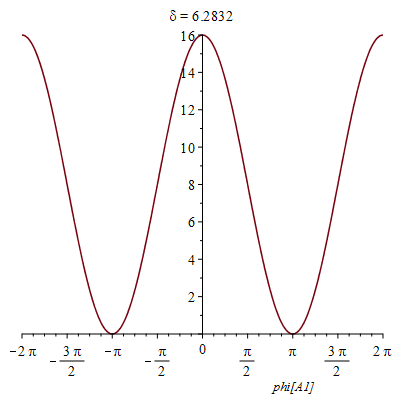 |
Man kann die Quellen also auch so einstellen, dass man nichts sieht :).
2. Mittelung für unkorrelierte Quellen in kohärenten Zuständen
Wenn sich die Phasenverschiebung δ der kohärenten Zustände nicht kontrollieren lässt, muss man über sie mitteln. Dann erhält man für die Koinzidenzzählrate
| > | I4cu=subs(pb=0,pa=0,EWs) |
|
|
(59) |
Mittelung (Integration über δ):
| > | int(EWs,delta=0..2*Pi)/(2*Pi) |
|
|
(60) |
| > | combine(%) |
|
|
(61) |
Was dem "klassischen Ergebnis" entspricht (α = β = 1):
| > | I4klass:=2*f[A]^2*f[B]^2*cos(-phi[A2]-phi[B1]+phi[B2]+phi[A1])+(f[A]^2+f[B]^2)^2 |
|
|
(67) |
Siehe auch die Box A im Original:

Animation zur Sichtbarkeit
| > | I4klani:=subs(f[A]=1, phi[A2]=0, phi[B1]=0, phi[B2]=0, I4klass) |
|
|
(68) |
 |
Im Gegensatz zu Fockzuständen (zwei Photonen) liegen die Minima nicht bei 0 und die maximale Sichtbarkeit beträgt nur 50%!
Zusammenfassung
a) Fock
1. Für die Zustände |n>|m> (mit n,m>1) ergeben sich "quasiklassische" Intensitätskorrelationen.
2. Für den Zustand |1>|1> kann man einen "echten Quanteneffekt" beobachten: die Sichtbarkeit des Interferenzmusters wird 1!
b) Glauber
1. Mit kontrollierbaren Glauber-Produktzuständen kann man "beliebige" Intensitätskorrelationen erhalten :)
2. Wenn sich die Phase nicht kontrollieren lässt - wie bei "klassischem/thermischem Licht" - ist die maximale Sichtbarkeit des Interferenzmusters nur 1/2.
Die zugehörigen Gleichungen lauten:

Anmerkung: Die Mode einer ebenen Welle ist eine "erste Näherung", die als Idealisierung nur in der Fernzone "erlaubt ist". Für eine realistischere Beschreibung kann man die Zeit- und Ortsabhängigkeit des E-Feldes in den Amplituden f berücksichtigen, die ja die Sichtbarkeit der Interferenz bestimmen. Ein pragmatischer Ansatz ist z.B. die Beschreibung der E-Feldstärke eines Photons durch ein Wellenpaket.
© Juli 2018, Dr. Michael Komma (VGWORT)
Siehe auch:
Matrixoptik | Doppelspalt und Dualismus | Quantenradierer | Photon am Doppelspalt | Gitter | Punktgitter | Kreuzgitter | Raumgitter | Beugung | Fresnelbeugung | Zeiger | Interferenz
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top