Zykloidenpendel
Augenwischer oder Scheibenwischer?
Ergänzung zu "Das Märchen vom harmonischen Oszillator im Schwerefeld"
Im Internet findet man zum Beispiel auch diese Märchen (Januar 2011):
"Im Gegensatz zum mathematischen Fadenpendel ist aber die
Bewegung exakt harmonisch, d.h. die Schwingungsfrequenz ist unabhängig von der
Amplitude." Oder:
"Beim Zykloidenpendel hat man nämlich unabhängig von der Auslenkung in der Tat
eine harmonische Schwingung. Das wußte übrigens schon Huygens! "
"In der Tat...": Die verschiedenen Punkte der Scheibenwischerblätter meines Autos haben alle die gleiche Schwingungsdauer. Schwingen sie also harmonisch?
Mal sehen, was Maple (und das Physics-Package) dazu sagt:
Lagrangefunktion
| > | L := T - V; |
![Typesetting:-mprintslash([`assign`(L, `+`(T, `-`(V)))], [`+`(T, `-`(V))])](zyklo_images/zyklolagrange_pub_1.gif){kind=small}
|
(1) |
Potentielle Energie
| > | V := m*g*z; |
![Typesetting:-mprintslash([`assign`(V, `*`(m, `*`(g, `*`(z))))], [`*`(m, `*`(g, `*`(z)))])](zyklo_images/zyklolagrange_pub_2.gif){kind=small}
|
(2) |
kinetische Energie
| > | T := 1/2*m*(v_ . v_); |
![Typesetting:-mprintslash([`assign`(T, `+`(`*`(`/`(1, 2), `*`(m, `*`(`^`(Norm(v_), 2))))))], [`+`(`*`(`/`(1, 2), `*`(m, `*`(`^`(Norm(v_), 2)))))])](zyklo_images/zyklolagrange_pub_3.gif){kind=small}
|
(3) |
Ortsvektor (allgemein)
| > | r_ := x*_i + z*_j; |
![Typesetting:-mprintslash([`assign`(r_, `+`(`*`(x, `*`(_i)), `*`(z, `*`(_j))))], [`+`(`*`(x, `*`(_i)), `*`(z, `*`(_j)))])](zyklo_images/zyklolagrange_pub_4.gif){kind=small}
|
(4) |
Nebenbedingung
| > | zyklo := [x = R*(phi(t)-sin(phi(t))), z = R*(-1+cos(phi(t)))]; |
![Typesetting:-mprintslash([`assign`(zyklo, [x = `*`(R, `*`(`+`(phi(t), `-`(sin(phi(t)))))), z = `*`(R, `*`(`+`(`-`(1), cos(phi(t)))))])], [[x = `*`(R, `*`(`+`(phi(t), `-`(sin(phi(t)))))), z = `*`(R, `*...](zyklo_images/zyklolagrange_pub_5.gif){kind=small}
|
(5) |
Ortsvektor neu
| > | r_:=subs(zyklo,r_); |
![Typesetting:-mprintslash([`assign`(r_, `+`(`*`(R, `*`(`+`(phi(t), `-`(sin(phi(t)))), `*`(_i))), `*`(R, `*`(`+`(`-`(1), cos(phi(t))), `*`(_j)))))], [`+`(`*`(R, `*`(`+`(phi(t), `-`(sin(phi(t)))), `*`(_i...](zyklo_images/zyklolagrange_pub_6.gif){kind=small}
|
(6) |
Geschwindigkeit neu
| > | v_ := diff(r_, t); |
![Typesetting:-mprintslash([`assign`(v_, `+`(`*`(R, `*`(`+`(diff(phi(t), t), `-`(`*`(cos(phi(t)), `*`(diff(phi(t), t))))), `*`(_i))), `-`(`*`(R, `*`(sin(phi(t)), `*`(diff(phi(t), t), `*`(_j)))))))], [`+...](zyklo_images/zyklolagrange_pub_7.gif){kind=small}
|
(7) |
Potentielle Energie neu
| > | V := subs(zyklo,V); |
![Typesetting:-mprintslash([`assign`(V, `*`(m, `*`(g, `*`(R, `*`(`+`(`-`(1), cos(phi(t))))))))], [`*`(m, `*`(g, `*`(R, `*`(`+`(`-`(1), cos(phi(t)))))))])](zyklo_images/zyklolagrange_pub_8.gif){kind=small}
|
(8) |
Lagrangefunktion neu
| > | L := combine(L, trig); |
|
(9) |
Die folgende Substitution ist nicht erforderlich, liefert aber handlichere Ergebnisse.
| > | L:=algsubs(1-cos(phi(t))=2*sin(phi(t)/2)^2,L); |
|
(10) |
Euler-Lagrange Gleichung
| > | EL:=diff(diff(L,diff(phi(t),t)),t)-diff(L,phi(t))=0; |
 
|
(11) |
Noch etwas umformen...
| > | EL:=expand(simplify(EL/(2*m*R^2*sin(phi(t)/2)))); |
|
(12) |
Dies ist bei näherem Hinsehen eine Schwingungsgleichung für cos(φ(t)/2), aber nicht für φ(t).
Lösung der DG mit allgemeinen Anfangsbedingungen
| > | soll:=dsolve([EL,phi(0)=phi0,D(phi)(0)=omega0],phi(t)); |
  
|
(13) |
Etwas übersichtlicher
| > | phipl:=rhs(expand(soll)); |
 
|
(14) |
Wie sieht das im Prinzip aus (als Funktion der Zeit)?
| > | plot([eval(phipl,[g=10,R=2,omega0=0,phi0=0]),eval(phipl,[g=10,R=2,omega0=0,phi0=Pi/2])],t=0..10); |
|
Nicht unbedingt harmonisch!
Im Folgenden ist die Anfangs(winkel)geschwindigkeit immer 0 und es wird nur der Startwinkel variiert. Dabei gehören die Kurven mit der größten Amplitude zum größten Startwinkel.
Wir testen zunächst φ(t) für verschiedene Startwinkel:
| > | plot([seq(eval(phipl,[g=10,R=2,omega0=0,phi0=sph]),sph=seq(Pi/10*i,i=0..9))],t=0..5.62); |
|
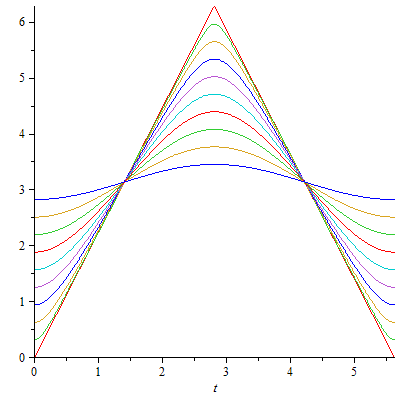
Immerhin - die Schwingungsdauer hängt nicht von der Auslenkung ab (Isochronie, Tautochronie). Aber nur für kleine Auslenkungen φ(0) ändert sich der Winkel sinusförmig (-cosinusförmig). Für die volle Auslenkung rollt das Rad gleichförmig hin- und zurück, d.h., die Winkelgeschwindigkeit ist dann eine Rechtecksfunktion:
Die Winkelbeschleunigung sieht so aus:
Das ist an den Umkehrpunkten der vollen Zykloide eine "Deltafunktion" (im Plot vertikal abgeschnitten). Es wird immer unharmonischer...
Wie sehen die Koordinaten aus (als Funktion der Zeit)?
| > | koord:=subs(soll,zyklo); |
      
|
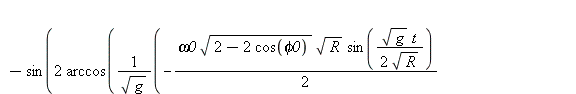
(15) |
x(t)
| > | xc:=subs(koord,x); |
    
|
(16) |
z(t)
| > | zc:=subs(koord,z); |
  
|
(17) |
Die Geschwindigkeiten und Beschleunigungen könnten auch interessant sein (Ausgabe unterdrückt, weil umfangreich):
| > | vx:=diff(xc,t): |
| > | vz:=diff(zc,t): |
| > | ax:=diff(vx,t): |
| > | az:=diff(vz,t): |
Der Differentialgleichung EL bzw. ihrer Lösung soll entnimmt man die Schwingungsdauer
| > | T:=2*Pi*sqrt(4*R/g); |
![Typesetting:-mprintslash([`assign`(T, `+`(`*`(4, `*`(Pi, `*`(`^`(`/`(`*`(R), `*`(g)), `/`(1, 2)))))))], [`+`(`*`(4, `*`(Pi, `*`(`^`(`/`(`*`(R), `*`(g)), `/`(1, 2))))))])](zyklo_images/zyklolagrange_pub_36.gif){kind=small}
|
(18) |
Dann können wir ja zur Tat schreiten:
| > | g:=10;R:=2; |
![Typesetting:-mprintslash([`assign`(g, 10)], [10])](zyklo_images/zyklolagrange_pub_37.gif){kind=small}
| |
![Typesetting:-mprintslash([`assign`(R, 2)], [2])](zyklo_images/zyklolagrange_pub_38.gif){kind=small}
|
(19) |
| > | omega0:=0; phi0:=0; |
![Typesetting:-mprintslash([`assign`(omega0, 0)], [0])](zyklo_images/zyklolagrange_pub_39.gif){kind=small}
| |
![Typesetting:-mprintslash([`assign`(phi0, 0)], [0])](zyklo_images/zyklolagrange_pub_40.gif){kind=small}
|
(20) |
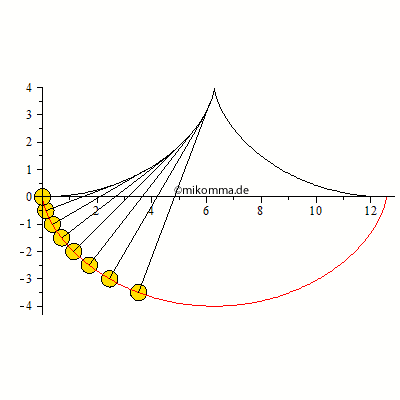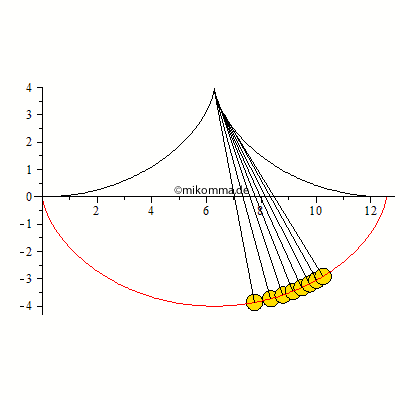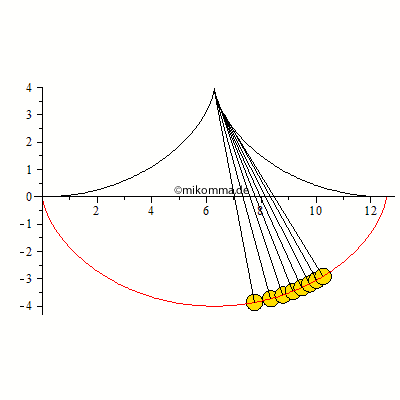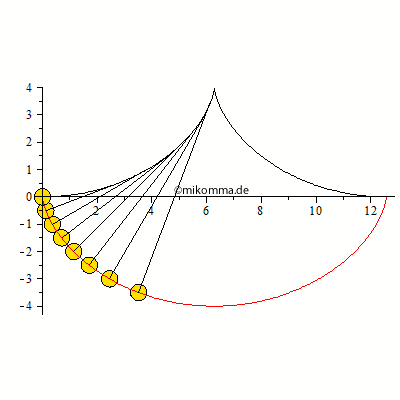
Ergibt das eine Zykloide?
| > | plot([xc,zc,t=0..T],scaling=constrained); |
|
Sieht so aus!
Wir sehen uns zunächst das x-t-Diagramm an
| > | phi0:='phi0': |
| > | plot([seq(xc,phi0=seq(Pi/10*i,i=0..9))],t=0..T); |
|
In x-Richtung ist die Schwingung nur für kleine Auslenkungen harmonisch.
Dies zeigt auch das vx-t-Diagramm
| > | plot([seq(vx,phi0=seq(Pi/10*i,i=0..9))],t=0..T); |
|
Und noch besser das ax-t-Diagramm
| > | plot([seq(ax,phi0=seq(Pi/10*i,i=0..9))],t=0..T); |
|
Im Vergleich dazu sind die Zeit-Diagramme für die Bewegung in z-Richtung eher langweilig, eben harmonisch...
| > | plot([seq(zc,phi0=seq(Pi/10*i,i=0..9))],t=0..T); |
|
| > | plot([seq(vz,phi0=seq(Pi/10*i,i=0..9))],t=0..T); |
|
| > | plot([seq(az,phi0=seq(Pi/10*i,i=0..9))],t=0..T); |
|
Phasendiagramme
Zunächst noch einmal die Bahnen für verschiedene Auslenkungen
| > | plot([seq([xc,zc,t=0..T/2],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
Mit einer künstlichen Verschiebung nach oben zur besseren Unterscheidung (Regenbogen einmal anders...):
| > | plot([seq([xc,zc+phi0/2,t=0..T/2],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
Und die Rückstellkraft als Fuktion der Auslenkung in x-Richtung
| > | plot([seq([xc,ax,t=0..T/2],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
Nicht gerade linear!
Und die Rückstellkraft als Fuktion der Auslenkung in z-Richtung
| > | plot([seq([zc,az,t=0..T/2],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
So sieht das Kraftgesetz für eine harmonische Schwingung aus!
Weitere Übungen zum Lesen von Phasendiagrammen. Lesehilfe: in den Plotbefehlen steht [Rechtsachse, Hochachse, Zeit=von..bis]. Im nächsten Diagramm wird also die Geschwindigkeit in x-Richtung (vx) über (und unter :-) der x-Koordinate (xc) dargestellt:
| > | plot([seq([xc,vx,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
| > | plot([seq([zc,vz,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
| > | plot([seq([xc,vz,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
| > | plot([seq([xc,az,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
| > | plot([seq([vz,az,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
| > | plot([seq([vx,az,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
| > | plot([seq([vz,ax,t=0..T],phi0=seq(Pi/10*i,i=0..9))],scaling=constrained); |
|
Fehlt noch etwas?
Ach ja - vielleicht noch ein ax-az-Diagramm zum harmonischen Ausklang...
Wie viele Phasendiagramme fehlen jetzt noch?
Und die Moral von der Geschicht? Kaum
vorstellbar, was Huygens alles gewusst hätte, wenn er Maple und ein Auto gehabt
hätte! Etwas ernsthafter bitte?
"Harmonische Schwingung" bedeutet im normalen Sprachgebrauch, dass sich die
Auslenkung als Sinus/Cosinus-Funktion darstellen lässt. Dies ist der Fall, wenn
für die Schwingung das lineare Kraftgesetz (quadratisches Potential) gilt.
Daraus folgt dann, dass die Schwingungsdauer einer harmonischen Schwingung nicht
von der Amplitude abhängt.
Folgende "Umkehrschlüsse" sind falsch:
1. Was isochron schwingt, schwingt harmonisch.
2. Was sich so parametrisieren lässt, dass es "der Schwingungsgleichung
gehorcht", schwingt harmonisch. Und natürlich:
3. Was sich im Schwerefeld auf einer Parabelbahn (= "quadratisches
Potential"???) bewegt, schwingt harmonisch.
© M. Komma 01/2011
Ja, ich weiß: Man könnte die Achsen der Diagramme auch beschriften. Für die html-Ausgabe
von Maple bin ich aber wirklich nicht verantwortlich...
Methode: Aufstellen der Differentialgleichungen mit
Lagrange (2. Art) und Maple. Lösung der Differentialgleichungen mit Maple, siehe
auch "
Newtons
Maschine". Die Differentialgleichung für die Zykloide lässt sich geschlossen
lösen.
Siehe auch:
Kreispendel
Das Märchen vom harmonischen Oszillator im Schwerefeld
Harmonischer Oszillator,
quantenmechanisch
Paulfalle,
Standard
Paulfalle,
Mechanisches Analogon |
Paulfalle, Mechanisches Analogon,
Details
HOME | Projekte | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top