Die blaue Kurve zeigt die Frequenzspektren, die rote den zeitlichen Verlauf der Schwingung. Das Produkt der Varianzen der beiden Verteilungen ist konstant ("Unschärferelation").

Frequenzkamm
Der optische Frequenzkamm ist nicht nur ein schönes Beispiel für Fouriertransformationen. Bekommt man ihn in den Griff - was derzeit immer besser gelingt -, kann man damit Frequenzen mit astronomischer Genauigkeit messen und kontrollieren, was bisher ungeahnte Folgen für uns alle haben wird - von der Grundlagenforschung (z.B. Astronomie) bis zur täglichen Anwendung (z.B. Signalübertragung).
Was muss man in den Griff bekommen? Die Fouriertransformation, also den Zusammenhang zwischen dem zeitlichen Verlauf einer Schwingung (oder Welle) und ihrem Frequenzspektrum. Allerdings handelt es sich dabei um ein Naturgesetz - und zwar ein ganz zentrales. Also sollte man statt "in den Griff bekommen" besser sagen "geschickt nutzen".
| Zunächst ein allseits bekannter
Zusammenhang: Zu einem aperiodischen Vorgang gehört ein
kontinuierliches Frequenzspektrum.
Dabei gilt: je
kürzer der Vorgang, desto breiter das Spektrum (Blitz, Schlag mit einem
Hammer).
Die blaue Kurve zeigt die Frequenzspektren, die rote den zeitlichen Verlauf der Schwingung. Das Produkt der Varianzen der beiden Verteilungen ist konstant ("Unschärferelation"). |

|
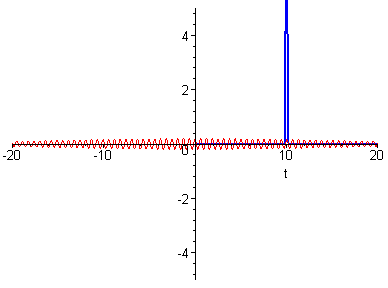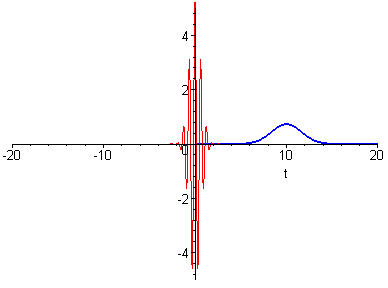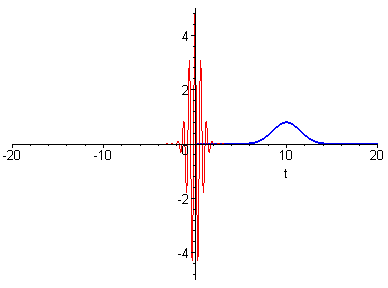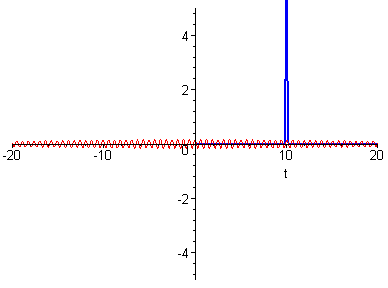
Umgekehrt gilt aber auch: Zu einem periodischen Vorgang gehört ein diskretes Frequenzspektrum (Linien).
In den folgenden Animationen ist jeweils links das Spektrum dargestellt und rechts die zugehörige Schwingung (willkürliche Einheiten).
| Frequenz | Zeit |

|
|
|
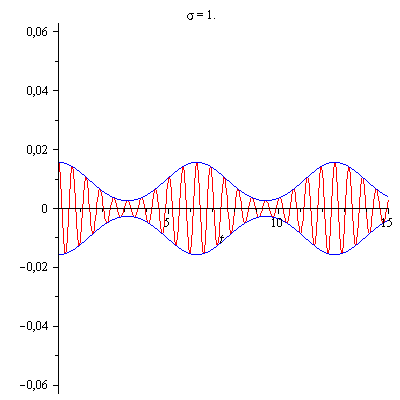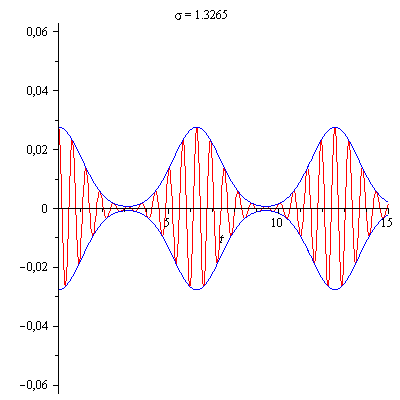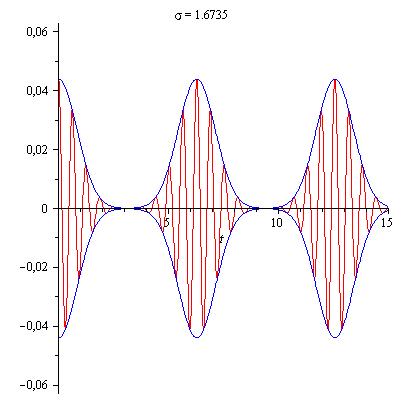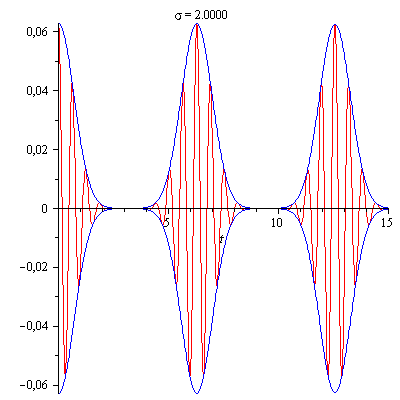
Zunächst wird bei festem Linienabstand (grün -
die Zinken des Frequenzkamms) die Breite σ der
Gaußverteilung (rot) verbreitert.
|
Dies hat zur Folge, dass wie bei einem
aperiodischen Vorgang die Dauer der Pulse (blaue
Einhüllende) abnimmt.
|

|

|
|
Verbreitert man den Abstand df der äquidistanten
Linien...
|
so wird der zeitliche Abstand der Pulse kleiner
(die Schwebungsfrequenz wird größer). Der
aufmerksame Betrachter stellt fest, dass nun die
Maxima der Einhüllenden (meistens) nicht mehr
mit einem Maximum der Schwingungskurve
zusammenfallen: Phasenschlupf.
|

|

|
| Im realen Experiment hat man keine unendlich scharfen Linien. Wie wirkt sich das aus? (Der Parameter b bedeutet: die grünen Linien haben die Breite σ/b.) | Die Einhüllende (schwarz) der Einhüllenden (blau) hat eine geringe Breite, wenn die Linien eine große Breite haben. Spätestens hier fängt die Experimentierkunst an! |
Gibt es also auch Mischformen? Natürlich! Die Natur hält sich nicht an unsere Idealisierungen "diskret - kontinuierlich"!
Und... natürlich kann man die Darstellungen auch von rechts nach links lesen: eine Seite ist die Fouriertransformierte der anderen - mit Maple erzeugt und in einem Maple-Worksheet interaktiv manipulierbar.
Siehe auch:
Fouriertransformation
mit Maple.
FFT mit
Maple
|
|
HOME | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top