• HOME
• Physik
  • Mathematik
  • Maple
• Mechanik
  • Kreispendel
  • Mathematisches Pendel
  • Kugelpendel
  • Harmonischen Oszillator
  • Oszillator, quantenmechanisch
  • Paulfalle mechanisch
  • Interferenz - elementar
  • Analemma
• Elektrizität
  • Hertzscher Dipol
  • Multipolstrahlung
  • Elektrostatische Felder
  • Geladene Teilchen in elektromagnetischen Feldern
• Optik
  • Gitter | Punktgitter | Kreuzgitter | Raumgitter
  • Fresnelbeugung | Lochblende | Rechteckblende | Dreieckblende | Kante
  • Zeiger | Interferenz | Interferenzmuster
  • Reflexion und Brechung | Licht im Medium | Brechungsindex | Dispersion
  • OAM-Wellen
• Atomphysik
  • Korrespondenzprinzip
  • H-Orbitals
  • Quantensprung in Zeitlupe
  • Elektrofluid
  • Rydbergatome
  • Paulfalle
• Quantenphysik
  • Quantensprung in Zeitlupe
  • Quantenradierer
  • What is a photon?
  • Photonenstatistik
  • Phasenraum
  • Harmonischer Oszillator
• Publikationen
  • Projekte
• English

Interferenz und Beugung

Leider ist der Export von Maple-Standard nach HTML nicht optimal.
PDF sieht besser aus.

Die Interferenz zweier Wellen lässt sich so beschreiben: 

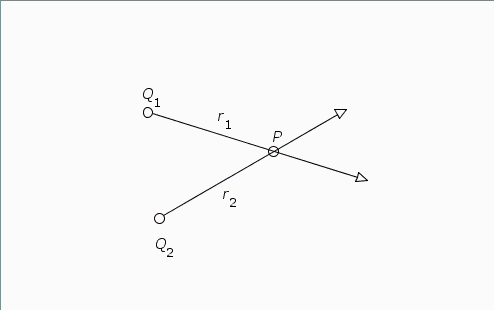
Von zwei Punkten Q₁  und Q₂ gehen zwei Wellen aus, die sich nach Durchlaufen der Strecken r₁ und r₂ im Punkt P treffen. Will man die Intensität im Interferenzpunkt P  (auf einem Schirm oder Detektor) wissen, so muss man das Betragsquadrat der resultierenden Amplitude berechnen: 

(1)

Die komplexe Schreibweise empfiehlt sich, weil dadurch die Mittelung der Intensität über die Zeit entfällt. Deshalb kann bei gleicher Frequenz (und kohärenten Wellen)  auch die Zeitabhängigkeit in diesem Zusammenhang weggelassen werden.
Die Amplituden A_i sind hier Skalare (Polarisation wird also nicht berücksichtigt), die für ebene Wellen (Näherungen siehe unten) konstant sind und für Kugelwellen mit 1/r abnehmen.
ist die Wellenzahl.
Wenn es sich bei Q₁  und Q₂ um zwei Sender handelt, müssen die Phasen _i bekannt sein.
Wenn es sich bei Q₁  und Q₂ um zwei Streuzentren (aber auch Elementarzentren) handelt, wenn also - wie in der Optik (oder allgemeiner elektromagnetischen Wellen) eigentlich immer der Fall - Q₁  und Q₂ von einer Lichtquelle L beleuchtet werden,   

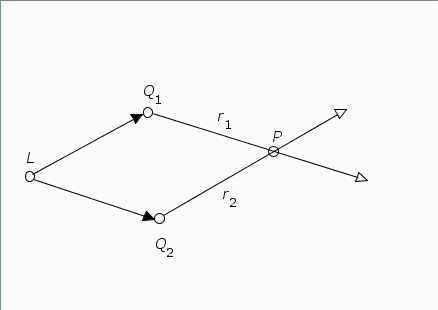
müssen die Phasen _i aus den Abständen von L zu Q_i berechnet werden.

• Die Interferenz zweier Wellen ist der elementare Baustein zur Berechnung von Interferenz und Beugung jeglicher Art.

(2)

Die Summation über endlich viele (punktförmige) Quellen kann immer exakt berechnet werden: Vielstralinterferenz, siehe

• Punktgitter

• Kreuzgitter

• Raumgitter

 Hat man unendlich viele Zentren (z.B. die Elementarzentren in einem Spalt endlicher Breite), so muss man integrieren: 

(3)

Wobei das Integral ∫_Q...dr_q über den Bereich Q der Quellen zu nehmen ist, also im schlimmsten Fall ein Mehrfachintegral mit dr_q = du_qdv_qdw_q für Q(u,v,w). Für diese Integrale ist leider keine Stammfunktion bekannt, also muss man numerisch integrieren oder Näherungen verwenden, siehe Beugung an einer

• Rechteckblende

• Dreieckblende

• Lochblende

• Kante 

Näherungen

Hier mehr vom Standpunkt der angewandten Mathematik aus: Wie lassen sich Interferenz und Beugung mit möglichst wenig Rechenzeit visualisieren - vielleicht sogar interaktiv (mit Maple)?
 

Man hat es mit folgenden Integralen zu tun (Fresnel-Kirchhoff):  

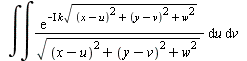
(4)

Dabei wurde (als Beispiel) folgendes Koordinatensystem verwendet: 

Die Quellen Q liegen in der u-v-Ebene. Der Interferenzpunkt P liegt in der zur u-v-Ebene parallelen x-y-Ebene, die zur Ebene der Quellen den Abstand w hat. Die Phase der Streuwelle ist hier nicht berücksichtigt (ebene Wellen treffen senkrecht auf die u-v-Ebene).

Die Integration bereitet Probleme, weil die Stammfunktionen nicht bekannt sind. Entweder man integriert numerisch oder man verwendet Näherungen.

Die erste Vereinfachung ist, mit ebenen Wellen zu rechnen, also in der Amplitude die 1/r-Abhängigkeit wegzulassen.
Aber auch für  

(5)

ist keine Stammfunktion bekannt.

Eine weitere Näherung besteht in der Reihenentwicklung der Wurzelfunktion (hier nur für eine Koordinate): 

(6)

Für k(x-u)² < w (also insbesondere für kleine Winkel) kann man versuchen, z.B. folgendes Integral zu berechnen: 

(7)

Als Beispiel wurde eine rechteckige Blende der Länge 2a und der Breite 2b gewählt (ohne von u und v unabhängige Faktoren). Nun gibt es zwei Möglichkeiten: 

1. Fresnelbeugung: 

Leider ist der Begriff Fresnelbeugung nicht exakt definiert. Die gängigste Verwendung ist: 

• Fresnelbeugung bedeutet "divergentes Licht" (punktförmige Lichtquelle wie in der Prinzipskizze oben) oder "Nahzone" (zu P konvergierendes Licht). Wenn man von "Fresnelnäherung" spricht und damit obige Näherung meint, wird die Gültigkeit dieser Näherung stark strapaziert, weil in der Nahzone meistens k(x-u)² > w gilt. (Empfohlene Literatur: Landau-Lifschitz II (Klassische Feldtheorie); Jackson Classical Electrodynamics.)

Immerhin gibt es in der "Fresnelnäherung" geschlossene Darstellungen für das Integral: 

(8)

Darin ist erf() die Fehlerfunktion, die sich auch in Fresnelintegrale umwandeln lässt (rechte Seite obiger Gleichung): 

(9)

Nun ja, sehr erfreulich sieht das auch nicht aus, zumal man für die Intensität noch das Betragsquadrat bilden muss. Aber im Vergleich zur numerischen Integration spart es Rechenzeit. 

2. Fraunhoferbeugung

Fraunhoferbeugung bedeutet paralleles Licht, also Fernzone. Hier sind sich alle einig. Noch erfreulicher ist, dass sich dann die Integrale stark vereinfachen:

In 

(10)

können die quadratischen Terme wegen x,u < w vernachlässigt werden und man erhält (wieder am Beispiel der Rechteckblende und unter Fortlassung von Proportionalitätskonstanten): 

(11)

Was "nichts weiter" ist als die "Fouriertransformierte der Blende" und sich vereinfachen lässt zu 

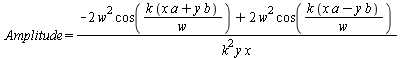
(12)

Das Beugungsmuster ist also "reziprok zum Beugungsobjekt": kleine Blende - starke Beugung! Aber das wussten wir ja schon immer... 

Siehe auch: Sterninterferometer

© M. Komma 10/2010

HOME | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top