Sterninterferometer

[Auszug aus stellarinter_pub1.mw]

https://www.eso.org/public/images/eso1907a/ https://cdn.eso.org/images/publicationjpg/eso1907a.jpg First Image of a Black Hole Credit: EHT Collaboration

Das erste Foto eines schwarzen Lochs - wie in den Zeitungen zu lesen war? Nein das erste Bild eines schwarzen Lochs, das aus Signalen von Radioteleskopen, die global verteilt waren, mit riesigem Rechenaufwand und ungeahnter Auflösung rekonstruiert wurde. Die Anordnung und die Technik nennt sich Event Horizon Telescope (EHT) und ist unter   https://iopscience.iop.org/journal/2041-8205/page/Focus_on_EHT
ausführlich beschrieben. Das EHT gehört zum Typ "Amplitudeninterferometer" (Michelson). Insbesondere Radioteleskope werden aber auch als "Intensitätsinterferometer" (Brown & Twiss - HBT) eingesetzt. In diesem Artikel geht es nicht um technische Details, sondern um das Funktionsprinzip dieser beiden Interferometertypen.

Gliederung 

Übersicht / Prinzip 

1. Doppelsternabstand 

1.1 Michelson 

1.2 Brown & Twiss       

2. Sterndurchmesser   

2.1 Michelson 

2.2 Brown & Twiss 

Text

Übersicht 

Ein reales Sterninterferometer sieht z.B. so aus

This image represents an overview of the VLT Interferometer as it was operated when the light beams from two of the 8.2-m telescopes were combined. The VINCI instrument that was used for the present test, is located at the common focus in the Interferometric Laboratory. Credit: ESO https://www.eso.org/public/news/eso0134/  https://cdn.eso.org/images/screen/eso0134a.jpg

Um das Wesentliche der verschiedenen Interferometertypen zu verstehen, verwenden wir folgende 

Prinzipskizze 

Ausgehend von zwei inkohärenten Quellen A und B, die sehr weit von der Ebene BT entfernt sind, erreichen Wellen (Licht oder Radio) die Punkte P1 und P2 (z.B. die Mitte zweier Spiegel). 

Der Betrag der Wellenvektoren kA und kB wird als gleich vorausgesetzt, bzw. durch Filter gleich gemacht. Kann man mit dieser Anordnung den Winkelabstand der beiden Quellen bestimmen? Es gibt zwei Möglichkeiten: 

1. Michelson-Sterninterferometer (Amplitudeninterferometer): Man bringt in der Ebene M (Brennebene des Teleskops) alle vier Wellen zur Überlagerung (Spiegel und Linsen nicht eingezeichnet), wodurch in der Umgebung von P ein (räumliches) Interferenzmuster entsteht, dessen Sichtbarkeit vom Abstand der Punkte P1 und P2 abhängt. (Anm.: Michelson-Sterninterferometer ist nicht zu verwechseln mit Michelson-Interferometer.) Mit den komplexen Amplituden A1, B1, A2 und B2 ist also der Mittelwert {...} von     

(1.1)

zu berechnen. 

2. Brown & Twiss Intensitätsinterferometer: Man misst in P1 und P2 die Intensität der Überlagerung der dort ankommenden Wellen, multipliziert beide Intensitäten, und bildet den Mittelwert: 

(1.2)

Das erste Verfahren kennt man auch von der "Interferenz am Doppelspalt", bzw. von der "Kohärenzbedingung": Ab welcher Größe des Beleuchtungsspalts verschwindet das Interferenzmuster? 

Das zweite Verfahren ist weniger bekannt, weil es sich dabei nicht um die "normale Interferenz" 1. Ordnung handelt (Überlagerung von Amplituden), sondern um eine Intensitätskorrelation, also Interferenz 2. Ordnung (Multiplikation von Intensitäten von überlagerten Wellen).

Ziel dieses Beitrages ist es, die Mathematik dieser beiden Verfahren in elementarisierter Form darzustellen. Darüber hinaus ist das Verständnis der beiden Typen von Sterninterferometern eine wichtige Voraussetzung für das Verständnis der Quantenoptik (man ersetze "Wellen" durch "Photonen"). 

1. Doppelstern 

Wir bezeichnen mit "Doppelstern" zwei punktförmige Lichtquellen mit geringem Winkelabstand (im Folgenden einfach "Abstand" genannt). 

1.1 Michelson 

Um den Abstand von Doppelsternen zu bestimmen, kann man wie oben beschrieben vorgehen. 

Mit den komplexen Amplituden A1,..,B2 ergibt sich die Überlagerung (resultierende elektrische Feldstärke) 

(2.1.1)

und die Intensität als Betragsquadrat 

(2.1.2)

Für die konkrete Berechnung führen wir die Phasen a1,..,b2 für die (optischen) Weglängen ein, sowie einen beliebigen Phasenunterschied pb der Quelle B zur Quelle A, über den gemittelt wird: 

	(2.1.3)

Damit erhält man für die Intensität 

(2.1.4)

Mittelung über die Phase pb:

(2.1.6)

Oder für gleiche Amplituden der Quelle a = b = 1: 

(2.1.7)

Die Summe der Cosinusfunktionen lässt sich auch als Produkt schreiben 

(2.1.9)

was dem üblichen Term für Interferenzstreifen 1 + V∙cos(x) entspricht. Nur ist hier die Sichtbarkeit V eine Schwingung mit der halben Differenzfrequenz (zweiter Cosinus), bzw. die Interferenzstreifen (mittlere Frequenz, erster Cosinus) sind wie bei einer Schwebung moduliert. 

Wir berechnen die Phasen a1, .. , b2: 

a) Am Ort der Spiegel (in der Ebene BT):

(2.1.11)

Dabei ist d der Abstand der Punkte P1 und P2, k der Betrag des Wellenvektors, α der Einfallswinkel der Strahlen von A und δ der Winkelabstand der beiden Quellen (Doppelsterne).   

Hier ist ein Beispiel (Animation mit δ):

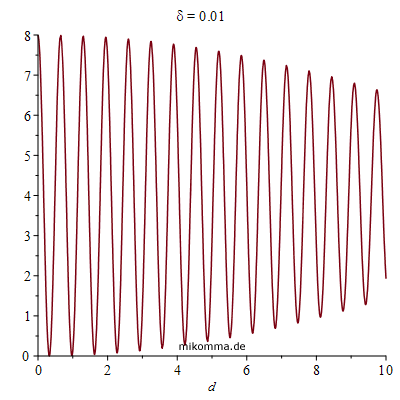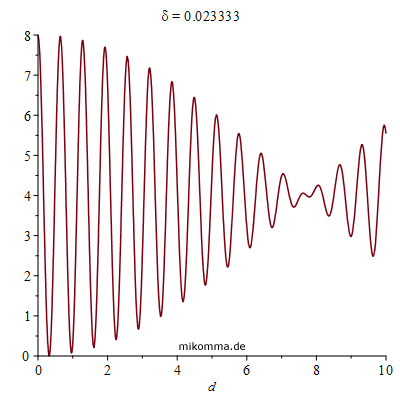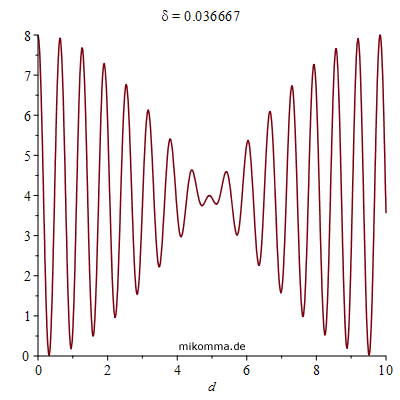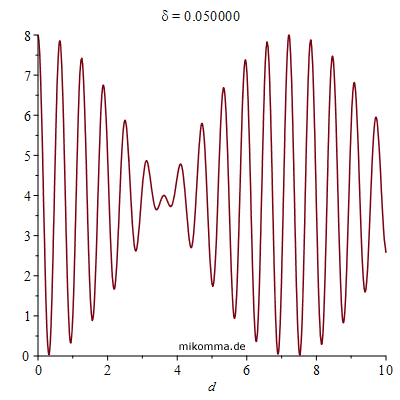Mit wachsendem Sternabstand δ wandert die "Nullstelle der Schwebung" zu kleineren Abständen d der Spiegel. Bei der Bestimmung des Sternabstands verändert man natürlich d bis die erste Nullstelle erreicht ist, und berechnet δ gemäß (für kleine Winkel):

(2.1.12)

b) In der Brennebene entsteht ein Interferenzmuster, das von der Strahlführung abhängig ist. Es kommt aber nicht auf das Interferenzmuster selbst an (Form, Streifenabstand usw.), sondern nur auf seine Sichtbarkeit. 

Berücksichtigt man noch die endliche Ausdehnung der Öffnungen (Spiegel), die aus einer punktförmigen Quelle "Beugungsscheibchen" macht, so sieht das Interferenzmuster etwa so aus, wenn man den Abstand von P1 und P2 (der Öffnungen oder Spiegel) verändert.

 Animation mit d: 

Im ersten Minimum der Sichtbarkeit wird die Animation für eine Sekunde angehalten. In dieser Animation erhöht sich die Frequenz der Interferenzstreifen mit dem Abstand der Spiegel (äußere Basislänge). In realen Teleskopen arbeitet man mit einer festen "inneren Basislänge" (z.B. Eintritt der Strahlen in das "grüne Rechteck" VINCI, Bild oben). Die äußere Basis ist also für die Sichtbarkeit zuständig und die innere für die Interferenzstreifen.

Leider wird die Sichtbarkeit des Interferenzmusters nicht alleine durch den Abstand der Spiegel bestimmt, sondern auch durch die Stabilität der Apparatur (Justage auf μm genau). Das Interferenzmuster "wackelt" aber auch, wenn das Licht außerhalb des Teleskops durch die Atmosphäre läuft: Seeing, was dann etwa so aussieht:  

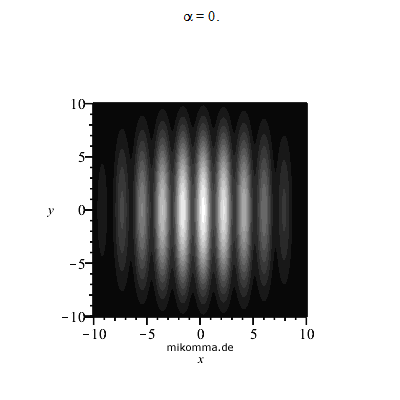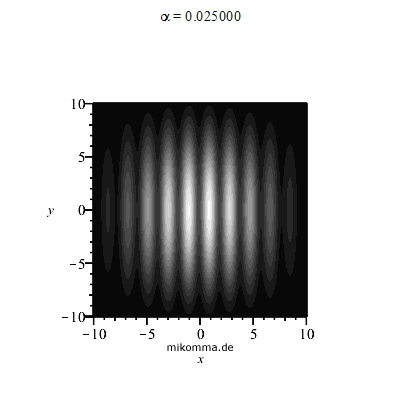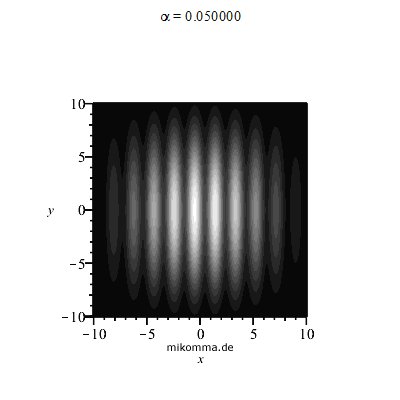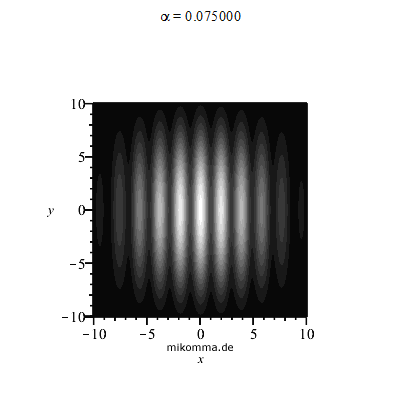1.2 Brown & Twiss (HBT), Doppelstern 

Die Rechnung wird hier nur verkürzt dargestellt, Bezeichnungen wie in 1.1.
Es muss der Term (1.2) 

(2.2.1)

berechnet werden. 

Da keine Amplituden-Interferenz beobachtet wird, interessieren nur Feldstärken in Detektor 1 und 2 (in den Punkten P1 und P2): 

	(2.2.2)

bzw. die Intensitäten

	(2.2.3)

Produkt der Intensitäten 

(2.2.4)

Mit Phasen (wie in 1.1.)

	(2.2.5)

Damit lautet das Produkt der Intensitäten 

(2.2.7)

Mittelung über pb:

(2.2.8)

ergibt vereinfacht 

(2.2.9)

oder mit den Winkeln von oben

(2.2.12)

Und für beide Amplituden = 1 

(2.2.13)

Zum Vergleich die Intensität im Michelson-Interferometer 

(2.2.15)

Der "hochfrequente" Term (die erste Cosinus-Funktion) ist verschwunden, und damit auch die Interferenzstreifen. Der "HBT-Schwebungsterm" hat die doppelte Frequenz, d.h., die Minima der Intensitätskorrelation (HBT) liegen bei den "Nullstellen der Michelson-Schwebung". 

Das HBT-Interferometer funktioniert also wie ein Demodulator! Es wird nur die blaue Kurve gemessen, die proportional zum Quadrat der Einhüllenden der Michelson-Interferenz ist, also die Sichtbarkeit "direkt" (mit Bestimmung des Sternabstands wie oben). Das hat den großen Vorteil, dass man von den Detektoren Kabel verlegen kann, sich also nicht um Lichtwege kümmern muss, bzw. die Detektorströme aufzeichnen und später (passend) multiplizieren kann. Aber natürlich geht dabei auch Information verloren, d.h., es lässt sich kein (hochauflösendes) Bild mehr rekonstruieren.

2. Sterndurchmesser 

Im Gegensatz zu der Bestimmung des Winkelabstands zweier Sterne hat man es bei der Bestimmung von Sterndurchmessern mit einer (einzigen) ausgedehnten Quelle zu tun. Aber auch hier kann man durch den Einsatz von zwei (oder mehr) Öffnungen (oder Teleskopen) mit variablem Abstand über den Kohärenzgrad 1. oder 2. Ordnung eine Winkelmessung durchführen, also den Sterndurchmesser bestimmen. 

2.1 Michelson 

Im Michelson-Interferometer überlagert man die Bilder zweier "Sternscheiben", d.h., aus der Summe der Amplitude zweier Punktquellen wird ein Integral über alle Punkte der ausgedehnten Quelle. (Siehe auch zwei Lochblenden)

Eine Sternscheibe mit konstanter Helligkeitsverteilung hat die gleiche Amplitudenverteilung (-> Fouriertransformierte, Fraunhofer-Näherung) wie eine Lochblende, auf die eine ebene Welle trifft.

(3.1.1)

Mit dem Durchmesser d der Scheibe (oder Blende), also

(3.1.2)

ergibt sich daraus die Intensitätsverteilung in der Fernzone (Brennebene)

(3.1.4)

(3.1.8)

an zwei Stellen: a) für die Sichtbarkeit VUD des Interferenzmusters, die im Vergleich zu (2.1.11) den "Schwebungsterm" ersetzt

(3.1.9)

mit dem Sternradius β. Für die Intensität UID ergibt sich

(3.1.10)

Für die Intensität ergibt sich also (mit Itel = Itel2D)

(3.1.12)

Die folgende Animation zeigt exemplarisch, wie sich das Interferenzmuster mit der Basislänge B verändert:

Im Unterschied zum Doppelstern ändert sich die Sichtbarkeit des Interferenzmusters nicht periodisch (so kann man einen nicht aufgelösten Doppelstern von einem einzelnen Stern unterscheiden), sondern klingt nach dem ersten Minimum stark ab.

In der Praxis arbeitet man mit einer festen "innere Basislänge", d.h., der Abstand der Interferenzstreifen bleibt konstant. In der folgenden Animation das B in der Cosinusfunktion von (3.1.12) konstant und die Animation wird im ersten und zweiten Minimum der Sichtbarkeit für eine Sekunde angehalten.

Aus Bildern dieser Art wurde das erste Bild eines schwarzen Lochs rekonstruiert...

2.2 Brown & Twiss , Sterndurchmesser

Zitat aus dem Originalartikel "Mon. Not. R. astr. Soc. (1967) 137, 375-392. THE STELLAR INTERFEROMETER AT NARRABRI OBSERVATORY—I, R. Hanbury Brown, J. Davis and L. R. Allen":

.

Mit anderen Worten: um den Durchmesser eines Sterns zu bestimmen, reicht es aus, die Korrelation 2. Ordnung zu bestimmen. Sie ist "... simply proportional to the square of the fringe visibility in a Michelson interferometer with the same baseline". Wie oben erwähnt, gehen dabei Details verloren.
Im Rahmen dieses Beitrags beschränken wir uns auf ein Rechenbeispiel:

Korrelation 2. Ordnung:

(3.2.1)

mit

(3.2.2)

also

(3.2.3)

kann man den Sterndurchmesser so bestimmen:

(3.2.4)

(3.2.5)

Woraus sich mit der ersten Nullstelle ergibt 

(3.2.6)