Polarisationsarten

Änderung der Polarisation von Licht durch doppelbrechende Medien

Mit Verzögerungsplättchen kann man aus linear polarisiertem Licht zirkular polarisiertes Licht machen und umgekehrt, sowie die Polarisationsebene von linear polarisiertem Licht drehen. Das funktioniert deshalb, weil sich in doppelbrechenden Medien Lichtwellen in zwei zueinander senkrechten Polarisationsebenen mit verschiedenen Geschwindigkeiten ausbreiten. Die folgende Prinzipskizze zeigt zwei Wellen, die sich in x-Richtung ausbreiten:

Dabei ist die "schnelle Welle" (blau) in z-Richtung (vertikal) polarisiert und die "langsame Welle" (schwarz) in y-Richtung. Beginn und Ende des Mediums sind durch graue Quadrate angedeutet, die die Ebenen x=0 und x=5 symbolisieren.

In obiger Prinzipskizze hinkt die langsame Welle nach dem Durchgang durch das Medium der schnellen Welle um eine viertel Wellenlänge hinterher: λ/4-Plättchen. Für alle folgenden Darstellungen gilt:

• Vor und nach dem Medium wird die (resultierende) Welle jeweils über eine Wellenlänge dargestellt.
• Die Wellenlänge der schnellen Welle ist gleich der Wellenlänge außerhalb des doppelbrechenden Mediums, nämlich gleich 1 (in passenden Einheiten).
• Die resultierende Welle wird als (rote) Ortskurve der E-Vektoren (grün) dargestellt.

λ/4-Plättchen

Wir beginnen mit der Umwandlung (Transformation) von linear polarisiertem Licht in zirkular polarisiertes Licht:

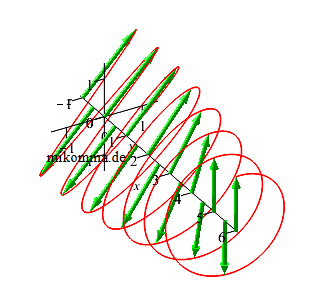Ist das einfallende Licht entlang der 1. Winkelhalbierenden der y-z-Ebene polarisiert, so entsteht eine Rechtsschraube. In der Optik nennt man dieses Licht rechtszirkular polarisiert (Schraubenkonvention).	Ist das einfallende Licht entlang der 2. Winkelhalbierenden der y-z-Ebene polarisiert, so entsteht eine Linksschraube. In der Optik nennt man dieses Licht linkszirkular polarisiert (Schraubenkonvention).
Natürlich bleibt die Welle nicht stehen, sondern schreitet in x-Richtung fort:
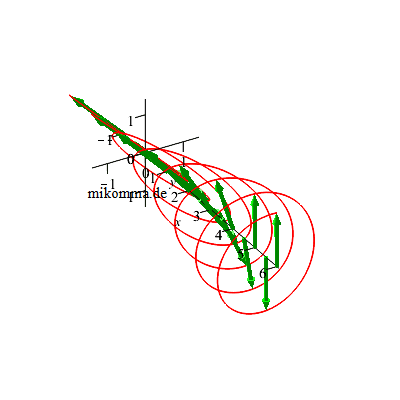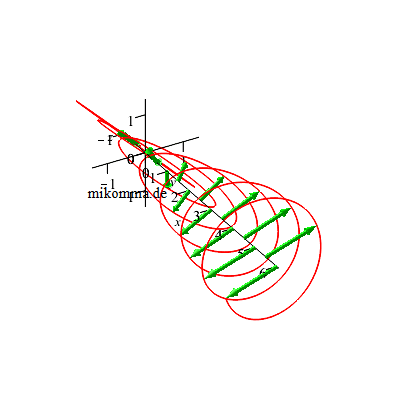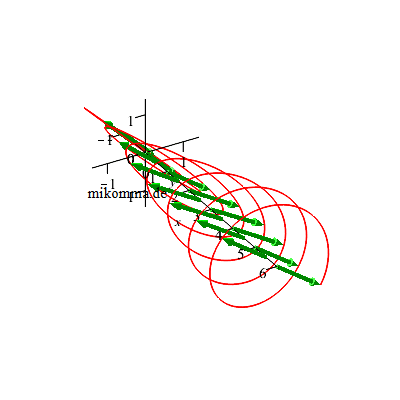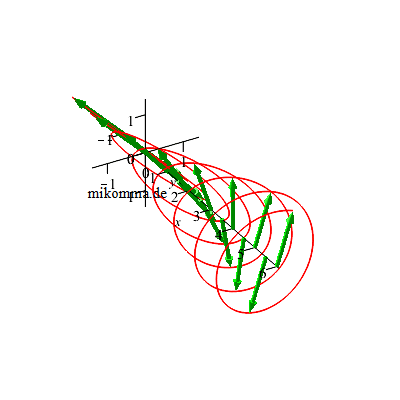Dabei dreht sich die Rechtsschraube (und die E-Vektoren) links herum (in Ausbreitungsrichtung gesehen). Weil das dem Spin eines Photons entspricht, nennt man in der Quantenphysik das austretende Licht linkszirkular polarisiert (Drehimpulskonvention).	Dabei dreht sich die Linksschraube (und die E-Vektoren) rechts herum (in Ausbreitungsrichtung gesehen). Weil das dem Spin eines Photons entspricht, nennt man in der Quantenphysik das austretende Licht rechtszirkular polarisiert (Drehimpulskonvention).

Egal in welcher Konvention: Man kann aus linear polarisiertem Licht zirkular polarisiertes Licht machen, wenn man das linear polarisierte Licht in zwei zu einander senkrechte Komponenten mit gleichem Betrag aufspaltet, und dafür sorgt, dass der Phasenunterschied der Komponenten 90° beträgt:

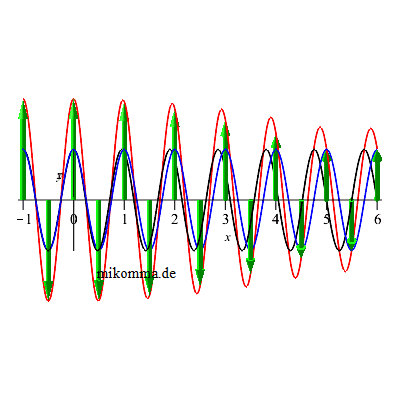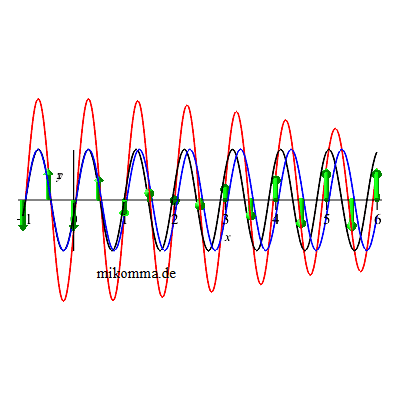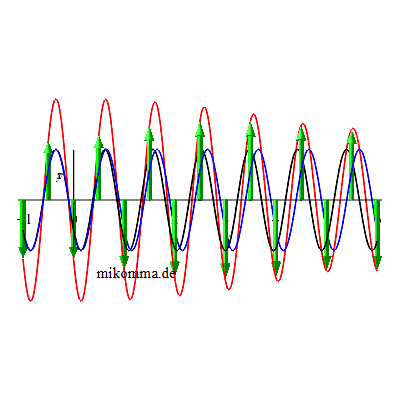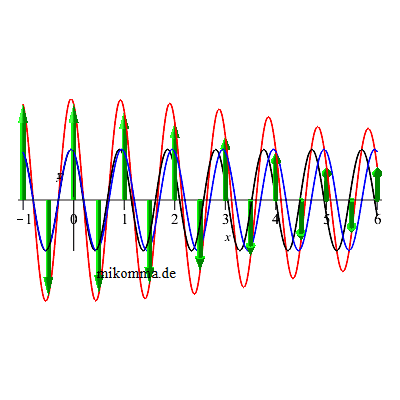Will man also aus natürlichem Licht zirkular polarisiertes Licht erzeugen, so schickt man es erst durch einen Filter für lineare Polarisation und dann durch ein λ/4-Plättchen.

Allerdings kommt es dabei auf die Orientierung des Polarisationsfilters zu zwei bevorzugten Polarisationsrichtungen des Plättchens an

Trifft man mit der Orientierung des Polfilters nicht genau eine der Winkelhalbierenden (s.o.), so entsteht "nur" elliptisch polarisiertes Licht:

Bzw., wenn man den Polfilter vor dem λ/4-Plättchen dreht, so entsteht dieses Licht (für t=0):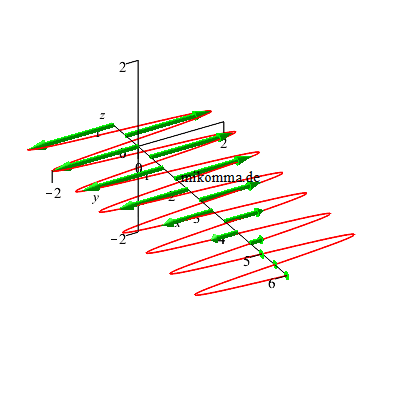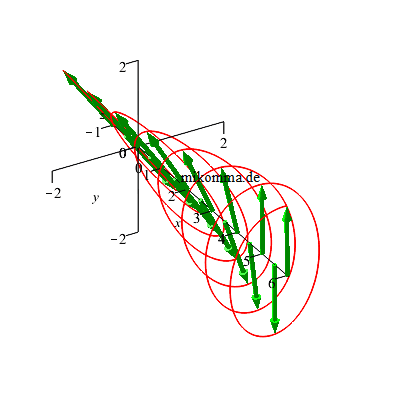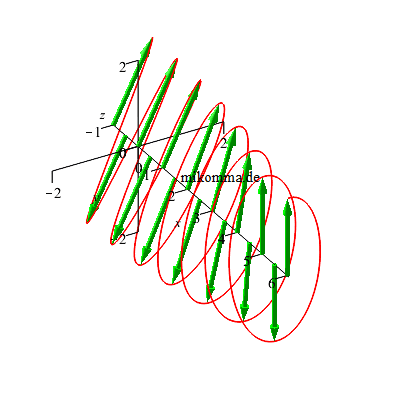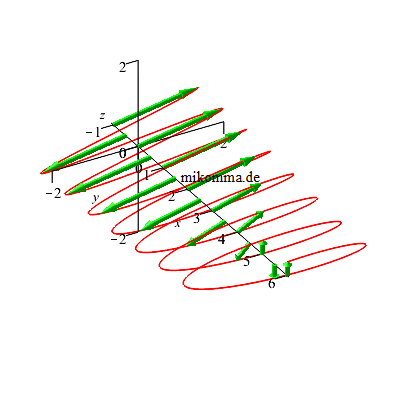

Blickt man in x-Richtung, so sieht man Lissajous-Figuren. Scherzfrage: Die Amplitude der zirkularen Schwingung ist kleiner als die Amplitude der linearen (oder elliptischen) Schwingung. Wie passt das zur Energieerhaltung?

Wenn umgekehrt zirkular polarisiertes Licht auf ein λ/4-Plättchen fällt, so entsteht linear polarisiertes Licht (man könnte obige Animationen auch rückwärts laufen lassen):

λ/2-Plättchen

Ein λ/2-Plättchen dreht die Polarisationsebene von linear polarisiertem Licht um 90°...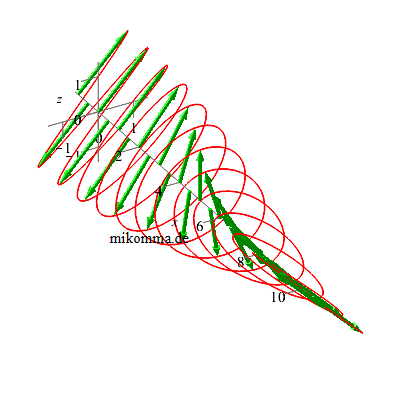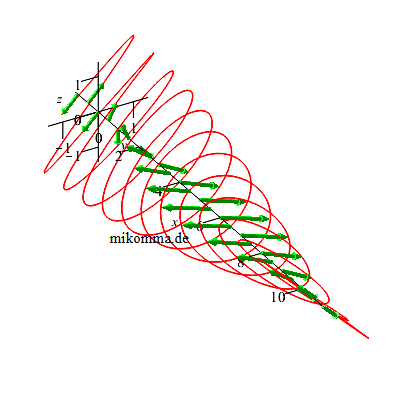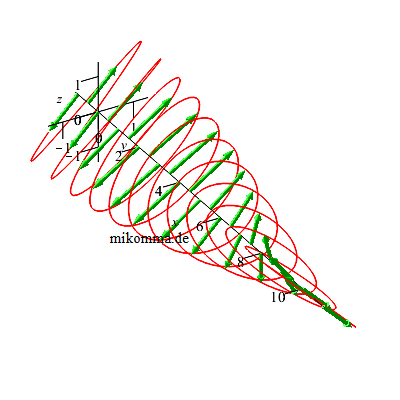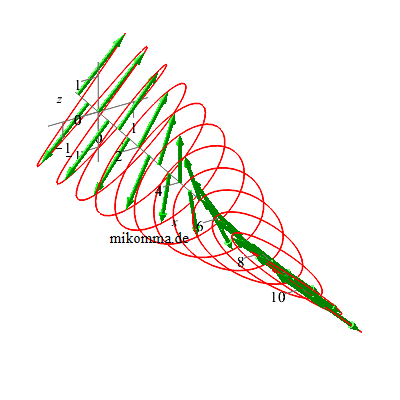

und kehrt den Drehsinn von zirkular polarisiertem Licht um.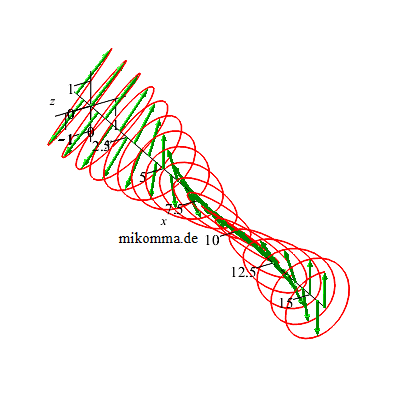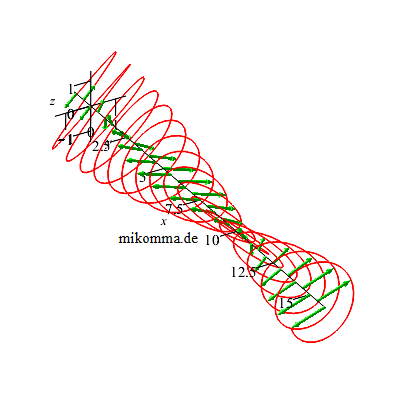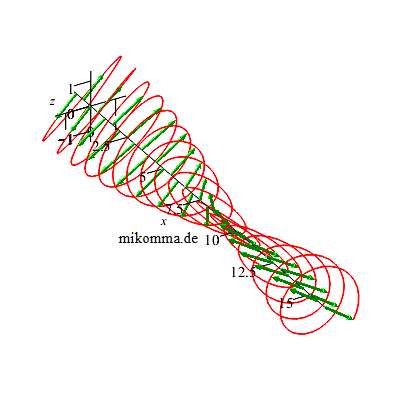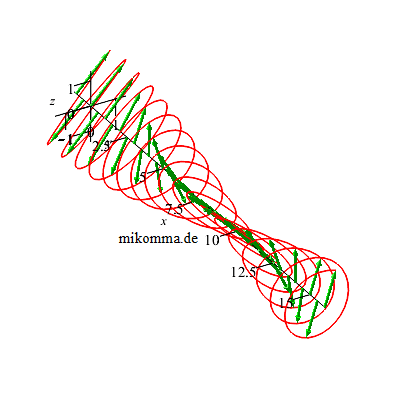

In der Animation oben rechts befindet sich das λ/2-Plättchen hinter einem λ/4-Plättchen. Das macht zusammen ein 3λ/4-Plättchen. Was macht also ein λ-Plättchen?

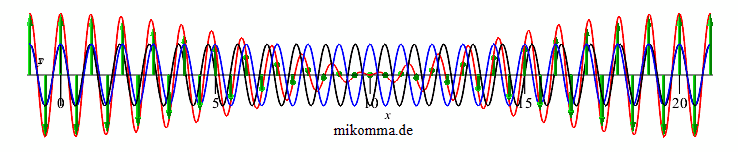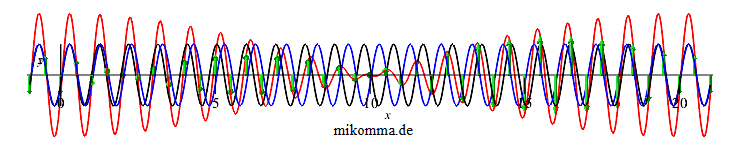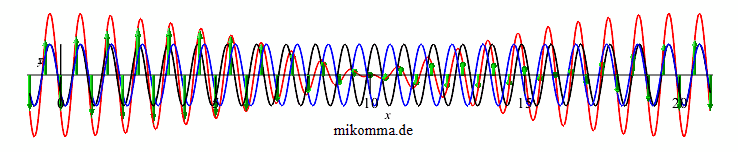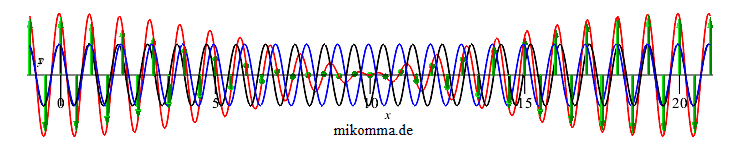
In der Darstellung oben liegt die Polarisationsrichtung der einfallenden Welle in der Bildschirmebene, die Polarisationsebenen der  schnellen (blau) und langsamen (schwarz) Welle sind also um 45° gegen die Bildschirmebene gedreht. Nach einem λ-Plättchen sind blau und schwarz wieder in Phase, ein λ-Plättchen bewirkt also nichts. Weshalb also diese Animation? Man kann ihr u.a.  entnehmen:

1. λ/4-Plättchen sind die Grundbausteine, mit denen man sich (zusammen mit Polfiltern) alles zum Thema lineare und zirkulare Polarisation zusammensetzen kann.
2. Bei der Ausbreitung einer Welle durch ein doppelbrechendes Medium entsteht unter den gemachten Voraussetzungen eine Schwebung.