Dispersion von Rechteckpulsen

Rechteckpulse sind eine mathematische Idealisierung. Um einen einzelnen Rechteckpuls räumlich oder zeitlich zu realisieren würde man ein kontinuierliches Spektrum unendlicher Bandbreite (Wellenzahl oder Frequenz) benötigen.

Der Zusammenhang zwischen Spektrum und Orts- oder Zeitfunktion ist immer durch die Fouriertransformation (kontinuierlich oder diskret) gegeben.

Die Fouriertransformierte einer Rechteckfunktion ist der Sinus cardinalis sinc(x) = sin(x)/x. Weil das Betragsquadrat dieser Funktion das Beugungsbild eines Spalts in der Fernzone darstellt, sagt man zu Sinc auch "Spaltfunktion". Beide Funktionen sind ohne Normierung dargestellt.
Wie verhalten sich Rechteckpulse in dispersiven Medien? 1. Rechteckiges Wellenpaket Schon bei einer linearen Abhängigkeit der Phasengeschwindigkeit von der Wellenzahl (siehe Dispersion) muss numerisch integriert werden, was im Vergleich zum Aufsummieren der Beiträge eines diskreten Spektrums die 10- bis 100-fache Rechenzeit kostet und selbst dann den Rechteckpuls nie als Rechteck darstellt, weil man immer mit einem Spektrum endlicher Breite rechnen muss. Die beiden folgenden Animationen wurden deshalb mit einem diskreten Spektrum (400 Linien) gerechnet.
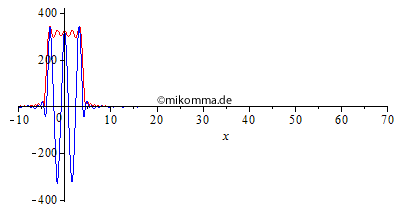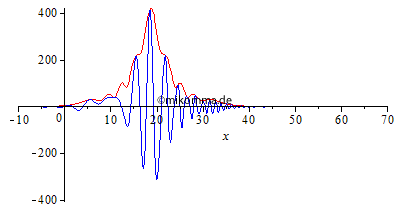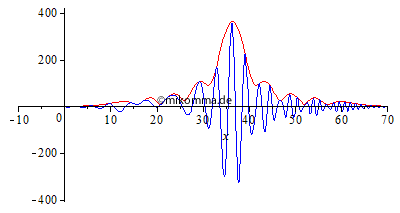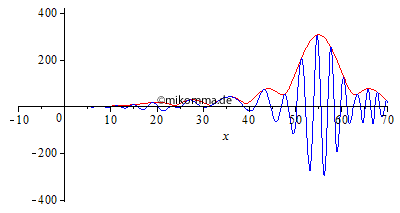
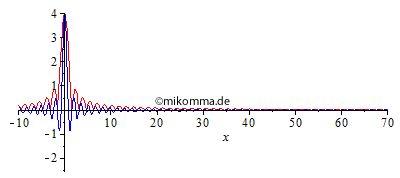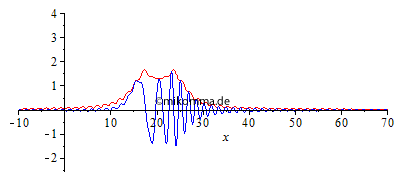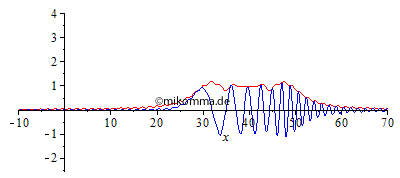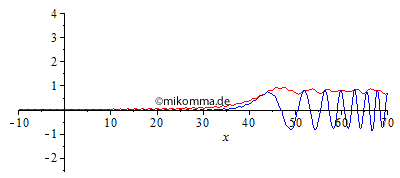
Normale Dispersion Die Einhüllende (rot, "Rechteck mit Restwelligkeit" zur Zeit 0 aus o.g. Gründen) zerfällt in eine Sinc-Kurve (Betrag) und bildet Vor- und Nachläufer aus. "Die Welle (blau) überholt die Gruppe (Einhüllende)", wobei Anteile mit großer Wellenlänge schneller laufen als kurwellige.
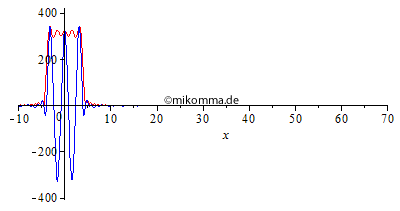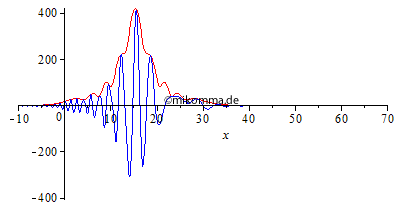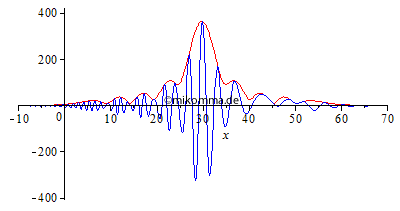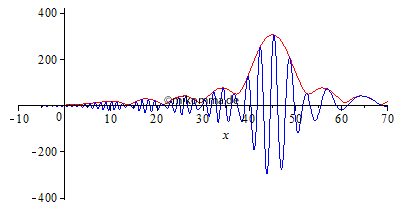
Anomale Dispersion "Sinngemäß"! Anmerkung: Darstellungen in "geeigneten Einheiten".

2. Rechteckiges Spektrum (Wellenzahlband)

In diesem Fall gibt es mit obigem Ansatz für die Dispersion eine "geschlossene Lösung" (Fresnelintegrale oder Fehlerfunktion), siehe " Moderne Physik, Fourier".

Normale Dispersion Die Sinc-Funktion mutiert zu einem Rechteck!
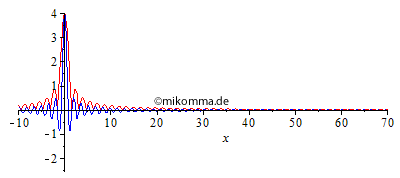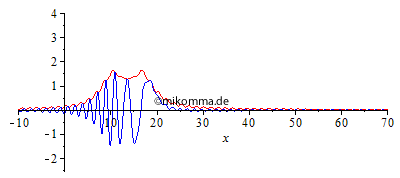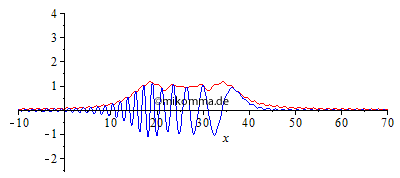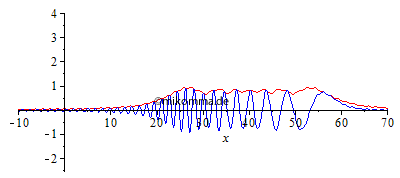Anomale Dispersion Sinngemäß! Anmerkung: Darstellungen in "geeigneten Einheiten".

Die Moral von der Geschicht?

Wer Rechtecke übertragen will, scheue den Sinus cardinalis nicht!