Zurück zum Inhalt

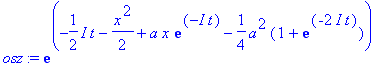
Oszillator nach Feynman

 

Kohärentes Paket (omega=hq=m=1)

 

>    osz:=exp(-I*t/2-1/2*(x^2-2*a*x*exp(-I*t)+1/2*a^2*(1+exp(-2*I*t))));

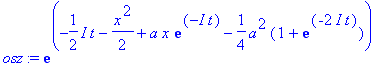
osz := exp(-1/2*I*t-1/2*x^2+a*x*exp(-I*t)-1/4*a^2*(1+exp(-2*I*t)))

 

>    osza:=evalc(abs(osz));

osza := exp(-1/2*x^2+a*x*cos(t)-1/4*a^2*(1+cos(2*t)))

 

>    a:=4: E:=a^2/2+1/2:

 

>    display([seq(display([plot(2*osza+E-(E-1/2)*sin(t)^2,x=-7..7),plot(x^2/2,x=-5..5,0..12)]),t=seq(2*Pi/96*i,i=0..95))],insequence=true);

[Maple Plot]

Die Psi-Funktion komplex:

 

>    display([seq(display([seq(pzeig(xx,t),xx=seq(k,k=seq(j/5,j=-25..25))),spacecurve([x,oszi,oszr],x=-5..5,axes=frame,numpoints=250,shading=ZHUE,thickness=2)]),t=seq(4*Pi*i/96,i=0..95))],insequence=true);

[Maple Plot]

 

>   

Feynmans Bewegungsgleichung

(Berechnung mit Propagator)

Anfangszustand, Gaußpaket um a ausgelenkt:

 

>    psi0:=(x,t)->exp(-(x-a)^2/2);

psi0 := proc (x, t) options operator, arrow; exp(-1/2*(x-a)^2) end proc

Propagator des harmonischen Oszillators

 

>    K:=(x,xa,t)->sqrt(1/(2*Pi*I*sin(t)))*exp(I/(2*sin(t))*((xa^2+x^2)*cos(t)-2*xa*x));

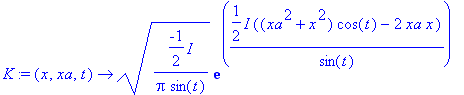
K := proc (x, xa, t) options operator, arrow; sqrt(-1/2*I/Pi/sin(t))*exp(1/2*I/sin(t)*((xa^2+x^2)*cos(t)-2*xa*x)) end proc

 

 

Faltung über alle Zwischenpunkte y

 

>    psi(x,t)=Int(K(x,y,t)*psi0(y,t),y=-infinity..infinity);

 

psi(x,t) = Int(K(x,y,t)*psi0(y,t),y = -infinity .. infinity)

 

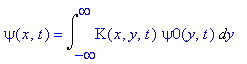
>    test:=int(K(x,xa,t)*psi0(xa,t),xa=-infinity..infinity) assuming(-csgn(1/2*I/sin(t)*cos(t)-1/2) = 1);

test := exp(1/2*I/sin(t)*(cos(t)^2*x^2*I-cos(t)*x^2*sin(t)-a^2*sin(t)*cos(t)-I*x^2+2*a*x*sin(t))/(cos(t)*I-sin(t)))*(-I/sin(t))^(1/2)/(-(cos(t)*I-sin(t))/sin(t))^(1/2)

Kann vereinfacht werden:

>    convert(test,exp);

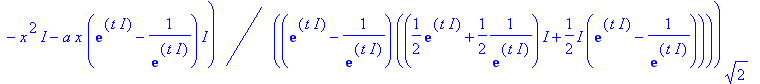
exp(-1/(exp(t*I)-1/exp(t*I))*((1/2*exp(t*I)+1/2*1/exp(t*I))^2*x^2*I+1/2*I*(1/2*exp(t*I)+1/2*1/exp(t*I))*x^2*(exp(t*I)-1/exp(t*I))+1/2*I*a^2*(exp(t*I)-1/exp(t*I))*(1/2*exp(t*I)+1/2*1/exp(t*I))-I*x^2-I*a...
exp(-1/(exp(t*I)-1/exp(t*I))*((1/2*exp(t*I)+1/2*1/exp(t*I))^2*x^2*I+1/2*I*(1/2*exp(t*I)+1/2*1/exp(t*I))*x^2*(exp(t*I)-1/exp(t*I))+1/2*I*a^2*(exp(t*I)-1/exp(t*I))*(1/2*exp(t*I)+1/2*1/exp(t*I))-I*x^2-I*a...
exp(-1/(exp(t*I)-1/exp(t*I))*((1/2*exp(t*I)+1/2*1/exp(t*I))^2*x^2*I+1/2*I*(1/2*exp(t*I)+1/2*1/exp(t*I))*x^2*(exp(t*I)-1/exp(t*I))+1/2*I*a^2*(exp(t*I)-1/exp(t*I))*(1/2*exp(t*I)+1/2*1/exp(t*I))-I*x^2-I*a...

 

>    simplify(%);

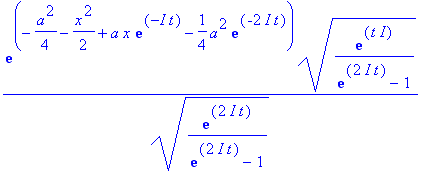
exp(-1/4*a^2-1/2*x^2+a*x*exp(-I*t)-1/4*a^2*exp(-2*I*t))*(exp(t*I)/(exp(2*I*t)-1))^(1/2)/(exp(2*I*t)/(exp(2*I*t)-1))^(1/2)

Oder

 

>    osz;

exp(-1/2*I*t-1/2*x^2+a*x*exp(-I*t)-1/4*a^2*(1+exp(-2*I*t)))

 

>   

Freies Teilchen (zum Vergleich)

 

>    Kfrei:=(x,xa,t)->1/sqrt(2*Pi*I*t)*exp(I*(x-xa)^2/(2*t));

Kfrei := proc (x, xa, t) options operator, arrow; 1/sqrt(2*I*Pi*t)*exp(1/2*I*(x-xa)^2/t) end proc

 

>    psi0(x,t);

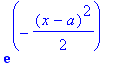
exp(-1/2*(x-a)^2)

 

 

>    pakfrei:=int(Kfrei(x,xa,t)*psiv(xa,t),xa=-infinity..infinity)    assuming(csgn(-1/2*I/t+1/2) = 1);

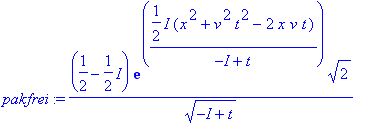
pakfrei := (1/2-1/2*I)*exp(1/2*I*(x^2+v^2*t^2-2*x*v*t)/(-I+t))*2^(1/2)/(-I+t)^(1/2)

 

>   

 

>    display([seq(display([seq(pzeig(xx,t),xx=seq(k,k=seq(j,j=-20..20))),spacecurve([x,psigim(x,t),psigre(x,t)],x=-20..20,axes=frame,numpoints=500,shading=ZHUE,thickness=2)]),t=seq(i/2,i=-20..20))],insequence=true);

[Maple Plot]

 

>   

Oder in 3D (psi über x-t)

 

>    plot3d(psiabs(x,t),x=-30..30,t=-30..30,axes=frame);

[Maple Plot]

 

 

>    plot3d(psigre(x,t),x=-30..30,t=-30..30,axes=frame,grid=[50,50]);

[Maple Plot]

 

>   

Zurück zum Inhalt

komma@oe.uni-tuebingen.de