Zurück zum Inhalt

Numerische Lösungen der stationären SGL

 

Numerisches Probierprogramm (Euler-Cauchy)

 

>    restart:
>    inte:=proc()
global x,u,us:
uss:=-c*(E-V(x))*u;
us:=us+uss*dx;
u:=u+us*dx;
x:=x+dx;
u;
end; 

Warning, `uss` is implicitly declared local to procedure `inte`

inte := proc () local uss; global x, u, us; uss := -c*(E-V(x))*u; us := us+uss*dx; u := u+us*dx; x := x+dx; u end proc

 

 

>    V:=x->a*x^2/2;

V := proc (x) options operator, arrow; 1/2*a*x^2 end proc

 

>    a,x,u,us,c,E,dx:=0.8/2/1.6022e-19,0,0,1,1.6022e-19*1.638e38,4.1434,5e-12;

 

 

>    for i to 500 do up[i]:=inte() od:

 

 

>    plot([seq([i,up[i]],i=1..500)],0..500);

a, x, u, us, c, E, dx := .2496567220e19, 0, 0, 1, .26244036e20, 4.1434, .5e-11

[Maple Plot]

 

>   

Es gibt eine Reihe von Möglichkeiten die numerischen Lösungen mit dsolve und odeplot darzustellen. (Das ist aber nicht sehr flexibel...)

 

>    restart:with(plots):
>    sgl:=diff(psi(x),x$2)=-2*(E-x^2/2)*psi(x);

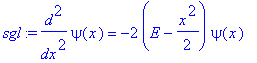
sgl := diff(psi(x),`$`(x,2)) = -2*(E-1/2*x^2)*psi(x)

 

>    sol:='sol':

 

>    sol:=dsolve({subs(E=7/2,sgl),psi(0)=0,D(psi)(0)=1},numeric);

 

 

>    sol(1);

[x = 1., psi(x) = .202176963456842884, diff(psi(x),x) = -.808707833863189118]

 

>    odeplot(sol,-5..5,numpoints=200);

[Maple Plot]

Funktion zur Übergabe von E (Randwerte müssen im folgenden Befehl eingegeben werden und sind dann fest):

 

>    solE:=Evar->dsolve({subs(E=Evar,sgl),psi(0)=0,D(psi)(0)=1},numeric);

solE := proc (Evar) options operator, arrow; dsolve({psi(0) = 0, D(psi)(0) = 1, subs(E = Evar,sgl)},numeric) end proc

 

>    solE(7/2)(1);

[x = 1., psi(x) = .202176963456842884, diff(psi(x),x) = -.808707833863189118]

 

>    odeplot(solE(11/2),-5..5,numpoints=200);

[Maple Plot]

 

>   

 

>    display([seq(odeplot(solE(E),-5..5,numpoints=200),E=1..2)],view=[-5..5,-1..1]);

[Maple Plot]

 

>   

Animation mit E als Parameter

 

>    display([seq(odeplot(solE(E),-5..5,numpoints=200),E=seq(1/2+i/5,i=0..50))],view=[-5..5,-1..1],insequence=true);

[Maple Plot]

 

>   

Variabler x-Wert für Randwert. Hintergrund: Man sollte mit der numerischen Lösung an beliebiger Stelle beginnen können - für geeignete Darstellungen, aber auch wegen Konvergenzfragen. (Mit symbolischen Lösungen ist das ziemlich kompliziert - wenn man auch noch beliebige Potentiale verarbeiten will)

 

>    solEx0:=(Evar,x0)->dsolve({subs(E=Evar,sgl),psi(x0)=0.001,D(psi)(x0)=0.001},numeric);

solEx0 := proc (Evar, x0) options operator, arrow; dsolve({subs(E = Evar,sgl), psi(x0) = .1e-2, D(psi)(x0) = .1e-2},numeric) end proc

 

>   

 

>    solEx0(7/2,-4)(1);

[x = 1., psi(x) = .977416850733246572e-2, diff(psi(x),x) = -.392376303616448139e-1]

 

>   

Animation, in der der Randwert der Energie angepasst ist

 

>    display([seq(odeplot(solEx0(E,-sqrt(2*E)*1.1),-5..5,numpoints=200),E=seq(1/2+i/5,i=0..100))],view=[-5..5,-0.01..0.01],insequence=true);

[Maple Plot]

 

>

Komplette Eingabe von Energie und Randwerten

 

>    solEpar:=(Evar,x0,x0w,dx0,dx0w)->dsolve({subs(E=Evar,sgl),psi(x0)=x0w,D(psi)(dx0)=dx0w},numeric);

solEpar := proc (Evar, x0, x0w, dx0, dx0w) options operator, arrow; dsolve({subs(E = Evar,sgl), psi(x0) = x0w, D(psi)(dx0) = dx0w},numeric) end proc

 

>    solEpar(7/2,0,0,0,1)(1);

[x = 1., psi(x) = .202176963456842884, diff(psi(x),x) = -.808707833863189118]

 

Plot

 

 

>    plot([seq(psil(E,-sqrt(2*E)*1.1,0.01,-sqrt(2*E)*1.1,0.01)(x)^2*2000+E,E=seq(1/2+i/20,i=0..50)),x^2/2],x=-3..3,0..4);

[Maple Plot]

 

Animation

[Maple Plot]

Zurück zum Inhalt

komma@oe.uni-tuebingen.de