Rutherford

Rutherfordstreuung

Mit Rutherfordstreuung meint man genau genommen die Streuung von Alphateilchen an Atomkernen. Die etwas weiter gefasste Bedeutung ist aber durchaus üblich: elastische Streuung elektrisch geladener Teilchen an einem festen Streuzentrum (ohne Berücksichtigung des Spins der Teilchen).

Im Ursprung befindet sich der positiv geladene Atomkern. Von unten nähern sich negativ geladene Teilchen (z.B. Elektronen), von oben positiv geladene Teilchen (z.B. Alphateilchen).Der Kern (das Streuzentrum) wird als unendlich große Masse betrachtet. Alle Teilchen haben die gleiche Energie aber verschiedene Drehimpulse (Stoßparameter). Wenn die Kraft anziehend ist (Kern - Elektron), haben die Teilchen im Perihel die größte Geschwindigkeit. Bei abstoßender Kraft haben sie im Perihel die kleinste Geschwindigkeit. Weitere Bilder und Animationen ...
Hier sind noch einmal die Elektronenbahnen mit etwas anderen Werten für die Drehimpulse zu sehen. Für jede Bahn bleibt der Drehimpuls (wie die gesamte Energie) während der Bewegung erhalten.
Wenn man nicht weiß auf welcher Seite die Elektronen den Atomkern passieren, sollte man zu einer symmetrischen Darstellung übergehen. Die meisten Elektronen werden in Vorwärtsrichtung gestreut. Es gibt ja beliebig hohe Drehimpulse (Stoßparameter). Nur bei einem fast zentralen Stoß wird das Elektron "reflektiert", kehrt also um. Berechnet man den Wirkungsquerschnitt Wq in Abhängigkeit des Streuwinkels klassisch (wie viele Bahnen entfallen auf ein Raumwinkelelement?) , so findet man Wq ~ 1/sin(Streuwinkel/2)^4, also Divergenz in Vorwärtsrichtung.
In der Quantenmechanik (oder Wellenmechanik?) zählt man nicht die Bahnen, sondern geht zu Wellen über. Wellenfronten stehen immer senkrecht auf Strahlen. Leider lassen sich die Wellenfronten (schwarz) in diesem Fall nicht so einfach berechnen, weil sich der Drehimpuls von Bahn zu Bahn ändert. Aber tatsächlich: In Kernnähe bewegt sich das Elektron schneller, hat eine kürzere Wellenlänge! Beim Betrachten des Bildes sollte man in Gedanken einen Schnitt entlang der negativen Hochachse machen: rechts davon bewegen sich die Wellen nach oben, links davon nach unten (einfallendes Teilchen - gestreutes Teilchen).
Auch hier wieder die symmetrische Darstellung: Von unten kommt die einfallende Welle des Elektrons, die im Coulombfeld des Atomkerns verzerrt wird ("Coulombwelle"). Asymptotisch (in großer Entfernung vom Kern) sieht man die Streuwelle, die insbesondere in Rückwärtsrichtung als Kugelwelle leicht zu erkennen ist. In Vorwärtsrichtung braucht man etwas mehr Phantasie: Für die Berechnung des Wirkungsquerschnitts müssen alle Wellen überlagert werden - das Elektron interferiert mit sich selbst, auch in der Nahzone... Die Wellenfronten haben aber nicht nur eine geometrische Bedeutung. Sie stellen vielmehr die Orte gleicher Wirkung dar und damit die Phase der Psi-Funktion des Elektrons bei der Rutherfordstreuung.
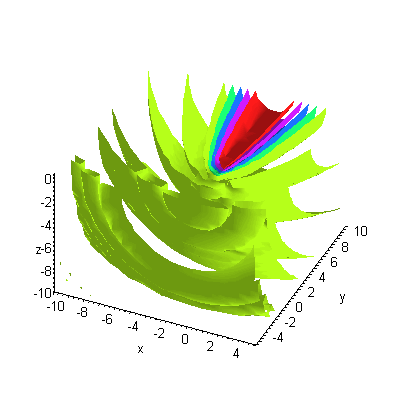
Und wenn man mit der Psi-Funktion den Wirkungsquerschnitt berechnet, kommt man auf das gleiche Ergebnis wie mit der klassischen Methode. Hier ist das Betragsquadrat der Psi-Funktion (eine Eigenfunktion des H-Atoms im Kontinuum) über der x-y-Ebene dargestellt.
Das Betragsquadrat einer Eigenfunktion gibt in diesem Fall nur Auskunft über einen "stationären Zustand", zeigt also keine Bewegung. Mit dem Realteil der Eigenfunktion kann man aber die Wellen laufen lassen (dargestellt ist das Quadrat des Realteils). Sehen Sie alles, was oben in der klassischen Behandlung der Rutherfordstreuung erwähnt wurde? Lokalisiert das Atom das Elektron oder das Elektron das Atom?
Natürlich ist die Streuung rotationssymmetrisch um die Achse in Richtung der "einfallenden Teilchen". Hier sind ein paar Impressionen vom Betragsquadrat der Psi-Funktion. Im Gegensatz zu den gebundenen Zuständen der H-Orbitals sind die Schalen nun nicht geschlossen sondern ähneln Rotationsparaboloiden.

Und hier ist die Formel: Darin ist hypergeom() die konfluente hypergeometrische Funktion (die imaginäre Einheit ist als großes I geschrieben).

Siehe auch: Zustände im Kontinuum

Moderne Physik mit Maple

komma_AT_oe.uni-tuebingen.de