Von der Matrixoptik zur Quantenoptik
Oder die "Algebraisierung von Interferenz"
(Auszug aus einem Maple-Worksheet)
Licht - Quanten |
Quantenoptik für Amateure
Leseproben:
Matrixoptik | Harmonischer
Oszillator | Quantisierung
des em. Feldes
Grundlagen
Beschreibung der Situation
Mit einem Mach-Zehnder-Interferometer (MZI) kann man die Interferenz von Lichtwellen untersuchen, ganz klassisch, aber auch "quantenmechanisch".

Auf den Eingang des ersten Strahlteilers ST1 trifft eine Welle in X-Richtung oder in Y-Richtung (oder beides). Der Strahlteiler verteilt die Welle(n) von seinen Eingängen auf zwei Ausgänge, je nach Typ des Strahlteilers mit einem "Phasensprung" der reflektierten Welle. Im Gegensatz zum Doppelspalt (oder Gitter oder noch allgemeiner einer "beugenden Anordnung") muss man nicht unendlich viele Richtungen berücksichtigen, sondern kommt mit zwei Richtungen X und Y aus. Es geht im Folgenden also nicht um die Interferenz zweier Kugelwellen (mit abstandsabhängiger Amplitude), sondern um die Interferenz zweier ebener Wellen. Um diese beiden Wellen "zur Interferenz zu bringen", werden sie (ihre Strahlen) geeignet geführt, z.B. mit Spiegeln S, und dann mit einem zweiten Strahlteiler (besser Strahlkombinierer) ST2 wieder auf eine (zwei) gemeinsame Richtung(en) X und Y geschickt (X und Y müssen räumlich nicht orthogonal sein). Wenn die die "Arme des Interferometers", also die Wege (in X- und Y-Richtung) und die Bauelemente ST und S identisch sind, verlässt eine Welle das MZI immer in die Richtung, aus der sie kam (warum wohl?). Das ändert sich allerdings, wenn man die Weglänge in einem Arm ändert, oder - äquivalent dazu - einen Phasenschieber PS in einem Arm unterbringt: Dann registrieren die Detektoren (oder "Schirme") D komplementäre Interferenzmuster (kohärentes Licht vorausgesetzt), wobei die Polarisation keine Rolle spielt.
Ist das zu langweilig? Dann nehmen wir die Polarisation der Lichtwellen hinzu! Mit einem Polarisator (oder Polarisationsdreher) P kann die Polarisation der Lichtwelle in einem Arm des Interferometers beeinflusst werden und mit einem Analysator A kann sie an einem Ausgang von ST2 gefiltert werden. Das geht natürlich auch in beiden Armen oder Ausgängen, aber wir wollen die Erörterung ja relativ einfach halten.
Man kann das alles mit reellen sin/cos-Wellen "durchrechnen" (wie in Quantenradierer), aber es gibt eine wesentlich elegantere Methode, die darüber hinaus auch noch tiefere Einblicke ermöglicht: Wellen in "komplexer Schreibweise", oder besser in einem komplexen Vektorraum, oder noch besser "Wellen in komplexen Vektorräumen", wobei der Plural z.B. auch für den Übergang vom Ortsraum zum Konfigurationsraum steht. Und genau das ist mit Algebraisierung von Interferenz gemeint: Das Wesentliche erfassen! Die ganzen rotierenden Zeiger, Wellen (mit "Bergen und Tälern"), Gangunterschiede, Polarisationsarten u.a.m. werden auf elementare (aber abstrakte) Bausteine eingedampft: Qubits!
Wie geht das?
Zwei Wellen werden zu einem Vektor zusammengefasst (die imaginäre Einheit wird hier als I geschrieben):
| > | w:=<c[x]*exp(I*(k*x-omega*t + phi[x])),c[y]*exp(I*(k*y-omega*t + phi[y]))>; |
](images/mzi_jones_2.gif) |
(1.1) |
Die Amplituden c können auch komplex sein. Wenn sich die Wellen nicht überlagern, erhält man das zeitliche Mittel der Intensität aus dem Skalarprodukt:
| > | w^* . w; |
| (1.2) |
| > | simplify(%) assuming real; |
| (1.3) |
Wenn sich die Wellen überlagern, "muss man (die Amplituden) erst addieren
| > | w[1]+w[2]; |
| (1.4) |
und dann quadrieren"
| > | combine(evalc(abs(%)^2)); |
| (1.5) |
um den "Interferenzterm" mit cos() zu erhalten. Im vorliegenden Fall lässt sich die Rechnung aber wesentlich vereinfachen: Man kann die Amplituden c = 1 setzen und den Gangunterschied x - y sowie den Unterschied der Phasen (für t = y = x =0) in einem einzigen Phasenunterschied Φ zusammenfassen:
| > | wn:=<exp(I*phi),1>; |
](images/mzi_jones_7.gif) |
(1.6) |
Skalarprodukt
| > | wn^* .wn; |
| (1.7) |
| > | simplify(%) assuming real; |
| (1.8) |
Interferenz
| > | combine(evalc(abs(wn[1]+wn[2])^2)); |
| (1.9) |
Mit diesen leicht überschaubaren Vektoren lässt sich praktisch alles berechnen, was in einem MZI passieren kann. Wir benötigen aber noch ein paar
Rechenregeln im komplexen Vektorraum
Zunächst ein paar Abkürzungen:
| > | macro(TP=KroneckerProduct): abs2:=proc(x) simplify(evalc(abs(x)^2)) end: |
| > | KX:=Ket(x): BX:=Bra(x): KY:=Ket(y): BY:=Bra(y): KH:=Ket(h): BH:=Bra(h): KV:=Ket(v): BV:=Bra(v): |
| > | XP:=<x[1],x[2]>: YP:=<y[1],y[2]>:
X:=<1,0>: Y:=<0,1>: PX:=X.X^*: PY:=Y.Y^*: |
Und Schreibweisen:
Wir schreiben einen (Spalten-) Vektor als Ket
| > | KX; |
| (1.10) |
oder in Komponentendarstellung
| > | KX=XP; |
](images/mzi_jones_12.gif) |
(1.11) |
und den dualen (Zeilen-) Vektor als Bra
| > | BX=XP^*; |
| (1.12) |
wobei der Querstrich das Konjugiertkomplexe bedeutet.
Dann schreibt sich das Skalarprodukt als Bra-Ket
| > | BY.KX=YP^*.XP; |
| (1.13) |
und das dyadische Produkt als Ket-Bra
| > | KX.BY=XP.YP^*; |
 |
(1.14) |
Das dyadische Produkt benötigen wir später für Operatoren.
Will (oder muss) man in mehr als einem komplexen Vektorraum rechnen, benötigt man noch das Tensorprodukt (oder Kroneckerprodukt):
| > | KX &ot KY = TP(XP,YP); |
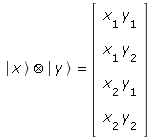 |
(1.15) |
Wofür in der Ket-Notation auch die Kurzschreibweisen
| > | KX*KY=Ket(xy); |
| (1.16) |
verwendet werden.
Zurück zum MZI: Den Vektor
| > | wn; |
](images/mzi_jones_18.gif) |
(1.17) |
können wir mit den Basisvektoren
| > | KX=X; |
](images/mzi_jones_19.gif) |
(1.18) |
| > | KY=Y; |
](images/mzi_jones_20.gif) |
(1.19) |
schreiben als
| > | exp(I*phi)*KX+KY = exp(I*phi)*X+Y ; |
](images/mzi_jones_21.gif) |
(1.20) |
Nun können wir also loslegen! Aber wie transportiert man die Wellen - dargestellt durch komplexe Vektoren - rechnerisch durch das MZI? Das geht mit Matrizen! Der einfachste Fall ist die
Einheitsmatrix
| > | Id:=IdentityMatrix(2); |
 |
(1.21) |
oder
| > | KX.BX + KY.BY = X.X^* + Y.Y^*; |
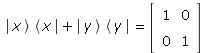 |
(1.22) |
Damit bleibt entlang der Wege alles wie es ist, z.B.:
| > | (KX.BX + KY.BY).KX = Id.X; |
](images/mzi_jones_24.gif) |
(1.23) |
Ist nicht besonders interessant, muss aber sein, damit die Wellen ihre Identität nicht verlieren :-)).
Nun brauchen wir einen
Strahlteiler
| > | ST:=<1,I;I,1>/sqrt(2); |
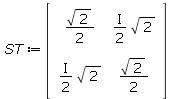 |
(1.24) |
der dafür sorgt, dass die durchgehende Welle und die reflektierte Welle jeweils die halbe Intensität haben, und die reflektierte Welle (z.B.) 90° phasenverschoben weiterläuft, also
| > | ST.KX=ST.X; |
](images/mzi_jones_26.gif) |
(1.25) |
und
| > | ST.KY=ST.Y; |
](images/mzi_jones_27.gif) |
(1.26) |
Sieht mit Maples Notation kompliziert aus, ist aber wirklich ganz einfach. Noch einfacher ist der
Spiegel (simultan in beiden Armen, ohne Phasensprung)
| > | S:=<0,1;1,0>; |
 |
(1.27) |
Der Spiegel vertauscht also X und Y:
| > | S.KX = S.X; |
](images/mzi_jones_29.gif) |
(1.28) |
Mit der Spiegelmatrix und der Identitätsmatrix lässt sich übrigens auch der Strahlteiler konstruieren:
| > | 'ST' = (Id + I*S)/sqrt(2); |
 |
(1.29) |
Ansonsten - oder mathematisch gesehen - ist der Spiegel ziemlich überflüssig (deshalb ignorieren wir auch den Phasensprung), aber physikalisch muss man die Strahlen eben zum nächsten Strahlteiler bringen (was natürlich auch mit Lichtleitern ginge).
Aber nun wird es wirklich interessant, denn wir haben es ja nicht mit Strahlen, sondern mit Wellen zu tun, die ihre Phase (zu deutsch: ihren Zustand) ändern können oder müssen:
Phasenschieber
| > | PS:=<exp(I*phi),0;0,1>; |
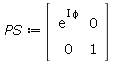 |
(1.30) |
| > | PS.KX = PS.X; |
](images/mzi_jones_32.gif) |
(1.31) |
| > | PS.KY = PS.Y; |
](images/mzi_jones_33.gif) |
(1.32) |
Die Phase wird hier also nur bei der X-Welle geschoben. So soll es ja auch sein!
Wir setzen alles zusammen:
MZI ohne Polarisation
Gesamtes Interferometer (ohne Berücksichtigung von Polarisation)

Die Matrizen der einzelnen Elemente (Strahlteiler usw.) müssen multipliziert werden. Das Produkt ist von rechts nach links zu lesen und ergibt
| > | MZ:=ST.PS.S.ST; |
 |
(2.1) |
Eine Welle in X-Richtung wird also überführt in
| > | MZ.X; |
](images/mzi_jones_36.gif) |
(2.2) |
Das ergibt am Ausgang in X-Richtung (Detektor rechts):
| > | X.(MZ.X); |
| (2.3) |
und in Y-Richtung (Detektor oben)
| > | Y.(MZ.X); |
| (2.4) |
Das bedeutet für die
Intensitäten:
Detektor D rechts:
| > | DR:=abs2(X.(MZ.X)); |
| (2.5) |
Detektor oben:
| > | DO:=abs2(Y.(MZ.X)); |
| (2.6) |
also zwei komplementäre "Interferenzmuster", bzw. Detektorströme, wenn der Phasenunterschied Φ variiert wird:
| > | plot([DR,DO],phi=-2*Pi..2*Pi); |
 |
Ja - das ist alles bekannt, auch ohne Bras und Kets und komplexe Vektorräume, aber wir haben nun unseren Algebrawerkzeugkasten sortiert, und am einfachsten Beispiel getestet. Wir nennen den Raum, in dem wir bisher gerechnet haben, den Raum R der Richtungen (X und Y).
Wie lassen sich polarisierte Wellen in einem MZI mit dieser Algebra behandeln?
MZI mit Polarisation
Polarisation
Wir nehmen wieder zwei Basisvektoren, z.B. für die Polarisationsrichtungen horizontal und vertikal:
| > | H:=<1,0>; V:=<0,1>; |
](images/mzi_jones_42.gif) |
|
], [Vector[column](%id = 18446744074372124294)])](images/mzi_jones_43.gif) |
(3.1) |
in einem zweiten Vektorraum P (für Polarisation). Damit wir diese Information in unserem MZI von oben unterbringen können, müssen wir im Produktraum R⊗P rechnen.
Eine horizontal polarisierte Welle in X-Richtung bekommt also den Basisvektor
| > | KX &ot Ket('H') = Ket('XH'); |
| (3.2) |
oder ausgeschrieben
| > | XH:=TP(X,H): |
| > | Ket('XH') = XH; |
 |
(3.3) |
ebenso
| > | XV:=TP(X,V):
Ket('XV') = XV; |
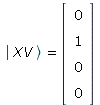 |
(3.4) |
(und die Varianten |YH> und |YV>).
Wenn sich die Polarisation der Wellen im MZI nicht ändert, erhalten wir natürlich das gleiche Ergebnis wie ohne Berücksichtigung der Polarisation. Aber wir wollen ja mehr:
Eine Änderung der Polarisation (ohne Absorption) kann am einfachsten mit einem Polarisationsdreher P (in einem Arm) berücksichtigt werden:
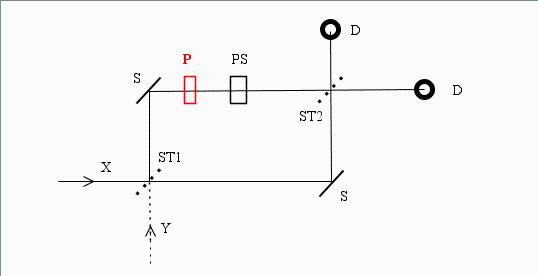
Wie macht man das - rein algebraisch?
Polarisationsdreher
Man nimmt eine "handelsübliche Drehmatrix":
| > | D2:=<cos(alpha),-sin(alpha);sin(alpha),cos(alpha)>; |
 |
(3.5) |
die das Koorditatensystem (im Raum der Polarisation) um den Winkel α dreht. (Anm.: α ist hier der "effektive Winkel" der Drehung. Mit Wellenlängenplättchen (λ/2) muss man den halben Winkel einstellen.) Also zum Beispiel
| > | 'D2'.Ket('H')=D2.H; |
](images/mzi_jones_49.gif) |
(3.6) |
Der Polarisationsdreher soll aber nur in einem Arm des Interferometers wirken. Das erreichen wir mit der direkten Summe von Dreh- und Einheitsmatrix (D2⊕Id):
| > | D4:=DiagonalMatrix([D2,Id]); |
 |
(3.7) |
Nun sieht die Matrix für unser MZI so aus:
MZI mit Polarisationsdreher
| > | MZP:=TP(ST,Id).TP(PS,Id).D4.TP(S,Id).TP(ST,Id); |
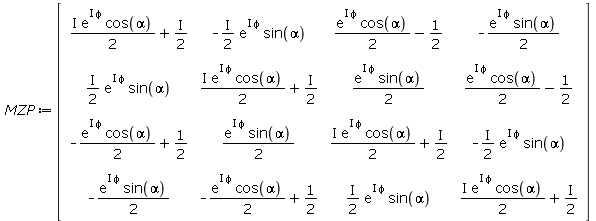 |
(3.8) |
Dabei wurden für die Rechnung im Produktraum die Matrizen für Strahlteiler, Spiegel und Phasenschieber jeweils um die Einheitsmatrix tensoriell erweitert.
Nun ja - so ist das eben mit Matrizen: sie neigen dazu, unübersichtlich zu werden. Aber wir haben ja ein CAS!
Im Produktraum sehen die Wellen nach dem MZI so aus:
Eine horizontal polarisierte Welle am X-Eingang von ST1 erscheint nach dem MZI als
| > | MZXH:=MZP.XH:
'MZP'. Ket('XH')=MZXH; |
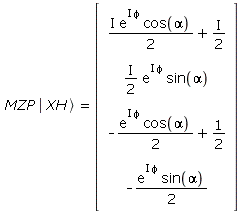 |
(3.9) |
und eine vertikal polarisierte Welle als
| > | MZXV:=MZP.XV; |
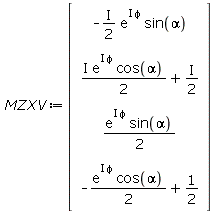 |
(3.10) |
Um von diesen "Wellen-Vektoren" im Produktraum zu Wellen im Richtungsraum zu kommen,
müssen wir auf den Unterraum der Richtungen projizieren, und eine Richtung (einen Detektor) auswählen.
Die Wahl einer Richtung, z.B. X, geschieht mit
| > | KX.BX=PX; |
 |
(3.11) |
also einer Projektionsmatrix, die aus dem dyadischen Produkt gebildet wird.
Erweiterung des Projektors (der Projektionsmatrix) auf den Produktraum
| > | PX4:=TP(PX,Id); |
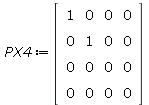 |
(3.12) |
Auf dem X-Ausgang erscheint also diese Welle:
| > | WX:=convert(PX4.MZXH,Vector); |
](images/mzi_jones_56.gif) |
(3.13) |
Mit der Intensität
| > | INTX:=simplify(WX^*.WX) assuming alpha::real,phi::real; |
| (3.14) |
| > | plot3d(INTX,phi=0..2*Pi,alpha=-Pi/2..0,shading=zhue); |
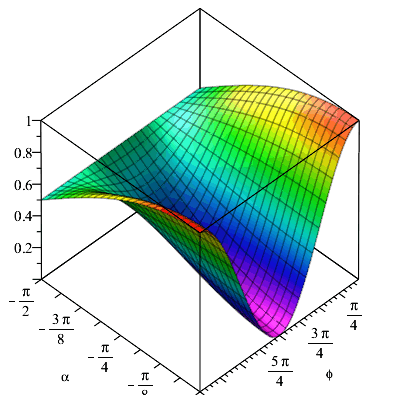 |
Im Vergleich zum "MZI ohne Polarisation" wird also die Sichtbarkeit des Interferenzmusters um den Faktor cos(α) verringert, wenn die Polarisation in einem Arm gedreht wird. Das liegt daran, dass sich durch die Drehung der Polarisationsebene einer Teilwelle die Art der Polarisation am Ausgang (bei der Überlagerung der Teilwellen) ändert und die resultierende Welle elliptisch polarisiert ist. Um die Details zu verstehen, muss man sich die Polarisationsellipsen ansehen - siehe Quantenradierer. So gesehen hat die "Algebraisierung von Interferenz" (oder der Jones-Formalismus) auch einen Nachteil: durch die "automatische Mittelung über die Zeit" gehen Informationen über Details verloren, was zu dem bekannten Trugschluss des "Quantenradierers mit Polarisationsfolien" führt.
Die Sichtbarkeit des Interferenzmusters lässt sich wieder herstellen (allerdings mit Verlust an Intensität), wenn man aus den elliptisch polarisierten Wellen, wieder linear polarisierte Wellen macht. Das geht mit einem
Analysator
oder Polarisationsfilter A, der z.B. hinter dem zweitem Strahlteiler in X-Richtung eingesetzt wird

Ein Analysator für die Polarisationsrichtung β (gemessen zur Richtung von H) wird durch folgende Matrix beschrieben
| > | A2:=<cos(beta)^2,sin(beta)*cos(beta);sin(beta)*cos(beta),sin(beta)^2>; |
 |
(3.15) |
Wie kommt man auf diese Matrix? Z.B. so (es gibt auch umständlichere Methoden):
Ein Polarisationsfilter für die Polarisationsrichtung β lässt den Vektor
| > | Pv:=<cos(beta),sin(beta)>:
Ket('P')=Pv; |
](images/mzi_jones_61.gif) |
(3.16) |
unverändert:
| > | A2.Pv; |
](images/mzi_jones_62.gif) |
(3.17) |
| > | simplify(%); |
](images/mzi_jones_63.gif) |
(3.18) |
Es gilt also
| > | Ket('P')*Bra('P')*Ket('P')=Ket('P'); # * statt . , um (falsche) Auswertung zu verhindern |
| (3.19) |
mit
| > | Ket('P')*Bra('P') = Pv . Pv^+; |
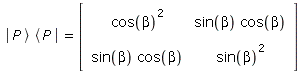 |
(3.20) |
Oder: |P> ist Eigenvektor von |P><P| mit Eigenwert 1.
Auf den Produktraum erweitert:
| > | A4:=DiagonalMatrix([A2,Id]); |
 |
(3.21) |
Wir setzen den Polfilter ein (rechnerisch)
| > | A4MZ:=A4.MZXH; |
 |
(3.22) |
Und wählen den X-Ausgang
| > | A4MZXH:=convert(TP(PX,Id).A4MZ,Vector); |
](images/mzi_jones_68.gif) |
(3.23) |
Das liefert am Detektor rechts die Intensität
| > | IAMZXH:=combine(simplify(A4MZXH^*.A4MZXH)) assuming alpha::real, beta::real, phi::real; |
| (3.24) |
Oder mit Mathematica vereinfacht:
| > | term:=1/4+(1/8)*cos(2*alpha-2*beta)+(1/8)*cos(2*beta)+(1/2)*cos(-beta+alpha)*cos(beta)*cos(phi); |
| (3.25) |
Beim Interferenzterm (cos(φ)) steht wieder die Sichtbarkeit als Funktion von α und β. Die anderen Summanden bestimmen die mittlere Intensität.
Für α = 90° (worst case) kann man das Interferenzmuster wieder sichtbar machen, wenn man die Stellung β des Polfilters ändert, allerdings nur bei halber Intensität:
| > | plot3d(subs(alpha=Pi/2,term),phi=0..2*Pi,beta=0..Pi,shading=zgrayscale); |
 |
Also für α = 90° maximale Sichtbarkeit für β=45° und 135° mit komplementärem Intensitätsverlauf.
Oder als Animation mit β beta als Parameter
| > | animate( plot3d, [term,phi=0..2*Pi,alpha=0..Pi], beta=0..Pi-Pi/40,frames=40,shading=zhue); |
 |
Oder mit α als Parameter
| > | animate( plot3d, [term,phi=0..2*Pi,beta=0..Pi], alpha=0..2*Pi-Pi/20,frames=40,shading=zhue); |
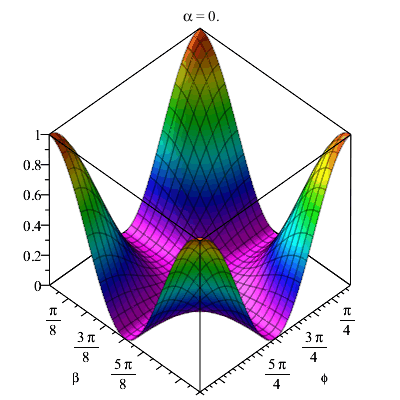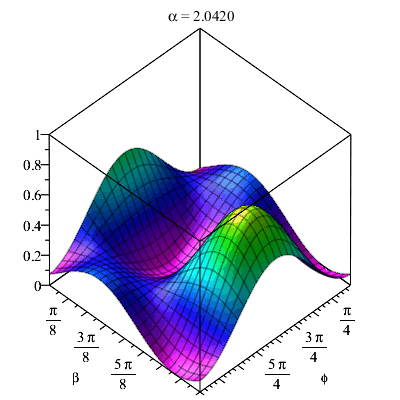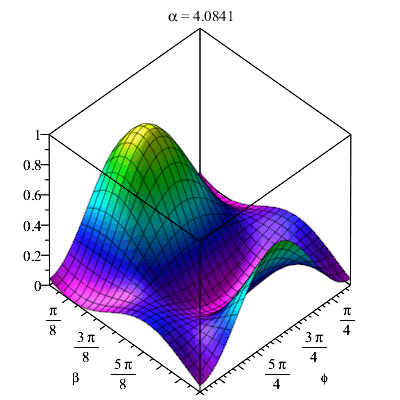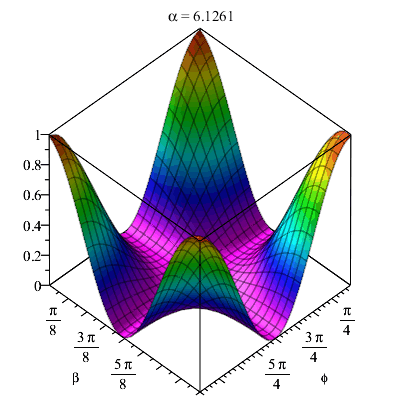 |
Alles klar?
Was passiert, wenn man statt des linearen Polfilters am Ausgang andere Apparate verwendet?
Man könnte ja z.B. dafür sorgen, dass die (resultierende) Welle am X-Ausgang rechtszirkular polarisiert wird. Das geht rechnerisch mit dem Operator für
Rechtszirkular
| > | RZ:=<1,I;-I,1>/2; |
 |
(3.26) |
Erweiterung auf den Produktraum
| > | RZ4:=DiagonalMatrix([RZ,Id]); |
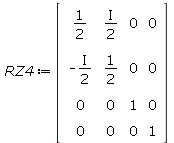 |
(3.27) |
liefert das
| > | ZMZXH:=RZ4.MZXH; |
 |
(3.28) |
auf dem X-Ausgang
| > | zamp:=convert(TP(PX,Id).ZMZXH,Vector); |
](images/mzi_jones_78.gif) |
(3.29) |
als Intensität
| > | zint:=zamp^*.zamp; |
 |
(3.30) |
| > | zint:=simplify(zint) assuming real; |
| (3.31) |
Ja - das Arbeiten mit komplexen Zahlen oder gar komplexen Vektoren ist in Maple nicht gerade benutzerfreundlich, liefert aber ein einfaches Ergebnis:
| > | zirk:=combine(evalc(zint)); |
| (3.32) |
| > | plot3d(zirk,phi=0..4*Pi,alpha=0..Pi,shading=zgrayscale); |
 |
D.h., der (erste) Poldreher verschiebt das Interferenzmuster. Sieht doch vernünftig aus!
Was lernen wir daraus?
1. Alle Interferenzerscheinungen am MZI, die durch die Überlagerung von Amplituden entstehen (man sagt dazu auch Interferenz 1. Ordnung), lassen sich klassisch beschreiben - egal mit welcher Lichtsorte (unpolarisiert oder eine beliebige Art der Polarisation).
2. Die mathematische Behandlung dieser Erscheinungen lässt sich "algebraisieren", was (im Ggs. zu Differentialgln.) den Formalismus stark vereinfacht.
Und wo bleibt die Quantenoptik?
Sie steckt schon in der Algebra der "klassischen Beschreibung": Man ersetze "Welle" durch "Zustand"! Das funktioniert sogar, wenn sich nur ein Photon in einem solchen Zustand befindet, denn das Photon kann (oder muss?) "mit sich selbst interferieren": wäre das nicht der Fall, könnten klassische Wellen nicht aus Photonen aufgebaut werden (rein rechnerisch :-)). Das bedeutet insbesondere, dass auch ein einzelnes Photon keinen bestimmten Weg nach einem Strahlteiler einschlägt (dennoch kann es an einem bestimmten Ort absorbiert werden). Wäre dies der Fall, könnte es - egal ob mit oder ohne Markierung durch Polarisation - nie mehr mit sich selbst interferieren. Vergessen wir also den Quantenradierer-Hokuspokus! Die Algebra der Zustände liefert wesentlich mehr als die Beschreibung des Zustandes eines Photons. Wie wäre es mit zwei Photonen?
MZI quantenoptisch
Biphoton
Anstatt die zwei Freiheitsgrade "Richtung" und "Polarisation" einer Welle (oder eines Photons) zu untersuchen, können wir doch auch zwei Wellen (oder zwei Photonen) im Richtungsraum nehmen und damit das MZI "füttern", also sozusagen im "Konfigurationsraum der Richtungen der beiden Wellen oder Photonen" rechnen - oder mit zwei Photonen in zwei Moden (der klassischen Wellen), also im Raum R⊗R:
Hier sind die Basisvektoren
| > | X1X2:=TP(X,X); Y1Y2:=TP(Y,Y); X1Y2:=TP(X,Y);Y1X2:=TP(Y,X); |
 |
|
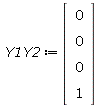 |
|
 |
|
![Typesetting:-mprintslash([Y1X2 := Matrix([[0], [0], [1], [0]])], [Matrix(%id = 18446744074339201742)])](images/mzi_jones_87.gif) |
(4.1) |
Und für jede Mode ein Strahlteiler bitte!
| > | ST4:=TP(ST,ST); |
 |
(4.2) |
Der Zustand |X1X2> (zwei Photonen auf dem X-Eingang) nach dem Produkt-Strahlteiler sieht so aus:
| > | ST4.X1X2; |
 |
(4.3) |
wird also zu |X1X2> + I*|X1Y2> + I*|Y1X2> - |Y1Y2>. Macht das Sinn? Mit klassischen Wellen nicht! Denn ob man eine oder zwei oder viele klassische Wellen auf einen Eingang eines Strahlteiler treffen lässt, macht keinen Unterschied: Die Wellen überlagern sich schon vor dem Strahlteiler zu einer einzigen Welle mit einer resultierenden Amplitude. Mit klassischen Wellen ist auch dieses Ergebnis nicht zu erklären:
Je eine "Welle" auf beiden Eingängen des Strahlteilers ergibt:
| > | ST4.(X1Y2+Y1X2)/sqrt(2); |
 |
(4.4) |
also |X1X2> + |Y1Y2>, sprich "zwei Wellen auf dem X- Ausgang oder zwei Wellen auf dem Y-Ausgang, aber nicht eine Welle auf dem X- und eine Welle auf dem Y-Ausgang". Das "können klassische Wellen" nicht! Zwei Photonen können das aber. Man nennt ihren Zustand dann verschränkt, weil sie - wie in diesem Beispiel (HOM-Dip) - den Strahlteiler immer gemeinsam auf einem Ausgang verlassen. Weil diese "geheime Absprache" auch in anderen Anordnugen über große Distanzen erfolgt, verzweifelte sogar Albert Einstein an dieser "spukhaften Fernwirkung".
Wir geben aber nicht auf und verfolgen den Weg (besser gesagt den Pfad) der Photonen im MZI quantenoptisch:
Spiegel im Produktraum
| > | S2:=TP(S,S); |
 |
(4.5) |
| > | S2.ST4.X1X2; |
 |
(4.6) |
= (|-X1X2> + I*|X1Y2> + I*|Y1X2> + |Y1Y2>)/2
Phasenschieber im Produktraum
| > | PS2:=TP(PS,PS); |
 |
(4.7) |
Man beachte, dass links oben die doppelte Phasendifferenz erscheint!
Die Matrix des MZI für Photonen sieht nun so aus
| > | MZ2:=ST4.PS2.S2.ST4; |
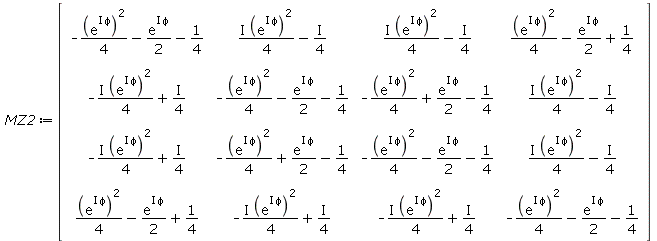 |
(4.8) |
Nun müssen wir nur noch für einen Input sorgen, z.B.:
Zwei Photonen auf dem X-Eingang
| > | psi:=MZ2.X1X2; |
 |
(4.9) |
Das liefert auf dem X-Ausgang die Amplitude
| > | X1X2^* .psi; |
 |
(4.10) |
| > | PXV:=convert(%,Vector); |
](images/mzi_jones_97.gif) |
(4.11) |
und die Intensität
| > | PXX:=abs2(PXV[1]); |
|
|
(4.12) |
Was an den Dreifachspalt erinnert:
| > | dreifach:=(-(1/4)*(exp(I*phi))^2-(1/4)*exp(I*phi)-1/4)*4/3; |
![Typesetting:-mprintslash([dreifach := `+`(`-`(`*`(`/`(1, 3), `*`(`^`(exp(`*`(I, `*`(phi))), 2)))), `-`(`*`(`/`(1, 3), `*`(exp(`*`(I, `*`(phi)))))), `-`(`/`(1, 3)))], [`+`(`-`(`*`(`/`(1, 3), `*`(`^`(ex...](images/mzi_jones_99.gif) |
(4.13) |
| > | Int3:=abs2(dreifach); |
|
|
(4.14) |
Für den Y-Ausgang ergibt sich:
| > | Y1Y2^* .psi; |
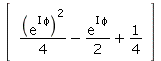 |
(4.15) |
| > | convert(%,Vector); |
](images/mzi_jones_102.gif) |
(4.16) |
| > | PYY:=abs2(%[1]); |
|
|
(4.17) |
und für die XY-Kombination:
| > | XY:=(TP(X,Y)+TP(Y,X))/sqrt(2); |
 |
(4.18) |
| > | XY^* . psi; |
 |
(4.19) |
| > | PXY:=abs2(convert(%,Vector)[1]); |
|
|
(4.20) |
| > | plot([PXX,PYY,PXY,Int3],phi,color=[red,green,blue,black]); |
 |
Im Vergleich zu "normalen Interferenzstreifen" fallen die Intensitäten PXX (rot) und PYY (grün) steiler ab und die Minima sind breiter. Tatsächlich handelt es sich um das Quadrat "normaler Intensitätskurven". Es tauchen aber keine Nebenmaxima auf wie beim Dreifachspalt (schwarz), der ja auch etwas "schärfere Maxima" liefert als der Doppelspalt. Vielleicht sollten wir uns überlegen, wohin uns der mathematische Formalismus geführt hat, und ob es überhaupt eine Realität dazu gibt? Die Antwort ist positiv:
Das Rechnen im Produktraum bedeutet auch eine Multiplikation der (komplexen) Amplituden und damit ein Produkt der Intensitäten, oder eine Intensitätskorrelation. Das macht sogar in der klassischen Physik einen Sinn, z.B. bei der Sterninterferometrie mit Radiowellen! Allerdings handelt es sich dabei nicht um Interferenz 1. Ordnung (Quadrat der Summe von Amplituden) sondern um Interferenz 2. Ordnung. Die "Intensitätsstreifen 2. Ordnung" sind nicht auf einem herkömmlichen Schirm (oder mit einem einzigen Detektor) sichtbar, sondern nur, wenn man die (Photo-) Ströme zweier Detektoren (Teilchendetektoren oder Radioantennen) multipliziert, also Koinzidenzmessungen macht.
Dazu muss (oder kann) man für PXX und PYY, also "zwei Photonen auf einem Ausgang", hinter einem weiteren Strahlteiler zwei Detektoren in Koinzidenz betreiben oder einen Detektor (oder Film als "Quantenschirm") verwenden, der nur auf die Energie von "zwei Photonen" reagiert.
Für PXY (blaue Kurve) reicht eine gewöhnliche Koinzidenzschaltung mit zwei Detektoren auf beiden Ausgängen. Und mit Erstaunen stellt man fest, dass diese Interferenzkurve die doppelte Frequenz hat. Aber vielleicht ist das ja gar nicht so erstaunlich, denn schließlich haben ja zwei Photonen gleicher Energie auch die doppelte Energie von einem.
Wenn man das Experiment "Biphoton im MZI" geschickt genug anstellt, kann man sogar mit einer einzigen Anordnung alle oben genannten Fälle "kontinuierlich durchsteuern":

Finden Sie in der Animation alle Kurven von oben wieder?
Bleibt noch der Fall
Je ein Photon auf beiden Eingängen
| > | psi:=convert(MZ2.X1Y2*sqrt(2), Vector); |
](images/mzi_jones_109.gif) |
(4.21) |
| > | X1X2^* .psi; |
](images/mzi_jones_110.gif) |
(4.22) |
| > | convert(%,Vector); |
](images/mzi_jones_111.gif) |
(4.23) |
| > | PXX:=abs2(%[1]); |
|
|
(4.24) |
| > | Y1Y2^* .psi; |
](images/mzi_jones_113.gif) |
(4.25) |
| > | PYY:=abs2(%[1]); |
|
|
(4.26) |
| > | XY:=(TP(X,Y)+TP(Y,X))/sqrt(2); |
 |
(4.27) |
| > | XY^* . psi; |
](images/mzi_jones_116.gif) |
(4.28) |
| > | PXY:=abs2(convert(%,Vector)[1]); |
|
|
(4.29) |
| > | plot([2*PXX,PXY],phi); |
 |
Das Ergebnis ist zwar nicht so vielfältig wie "zwei Photonen auf einem Eingang", zeigt aber doch die quantenmechanische Besonderheit der "Frequenzverdoppelung": Ein Photonenpaar (zwei verschränkte Photonen gleicher Energie, genauer: mit in der Summe fester Energie) "kann sich wie ein Photon der doppelten Energie benehmen", wenn man Intensitätskorrelationen misst. Die "normale Interferenz eines Photons mit sich selbst" würde Interferenzstreifen der halben Frequenz erzeugen.
© Juni 2014, Dr. Michael Komma (VGWORT)
Literatur: Enrique J. Galvez: Qubit quantum mechanics with correlated-photon experiments.
