Über die Ursprünge des Quantensprungs
Wie auch große Geister im Dunkeln tappen, wenn Experimente etwas völlig Neues ans Tageslicht bringen...
Zitate (gelb) aus Arnold Sommerfeld, Atombau und Spektrallinien II. Band, S. 495 ff., Vieweg & Sohn 1967

Vorweg eine Anmerkung zum Begriff "Bremsstrahlung" (klassische Beschreibung): Ein freies Elektron wird beim Vorbeiflug am Atomkern bis zum Scheitel der Hyperbelbahn (Perihel) beschleunigt und dann wieder abgebremst. Verliert es dabei insgesamt keine Energie, so wird es elastisch gestreut und ändert nur seine Richtung (" Rutherfordstreuung"). Dies ist der weitaus häufigste Prozess, der aber hier nicht gemeint ist. Bremsstrahlung bedeutet, dass das Elektron Energie in Form von elektromagnetischer Strahlung abgibt, also nach dem "inelastischen Stoß" langsamer ist als vorher.
Vor etwa 100 Jahren (1911) waren die theoretischen Physiker mit einem Problem konfrontiert, das sich nicht mit der klassischen Elektrodynamik lösen ließ: Eigentlich müsste eine einmalig beschleunigte (gebremste) Ladung (Kathoden-Strahlen = Elektronen) ein kontinuierliches Spektrum (= weißes Röntgenlicht) elektromagnetischer Wellen abstrahlen, in dem beliebig hohe Frequenzen vorkommen. Aber das Spektrum der Bremsstrahlung hat eine "kurzwellige Grenze", bzw. eine maximale Frequenz, für die eine "Quantengleichung" gilt:

Das ist ja auch vernünftig, denn mehr als die kinetische Energie des Elektrons kann bei der Bremsung nicht abgestrahlt werden. Das Problem ist nur: Warum gibt es eine obere Schranke für die Frequenz der Strahlung?
"Der Verfasser" ( = Sommerfeld) entwarf eine provisorische Theorie:

Mit diesem "ad hoc ersonnenen Postulat" erhielt Sommerfeld auch die richtige Größenordnung der abgestrahlten Intensität der Bremsstrahlung, aber das Problem der kurzwelligen Grenze war damit nicht gelöst. Auch Einsteins Vorschlag, "das Quantenmäßige in die Strahlung zu verlegen", führte nicht zum Erfolg:

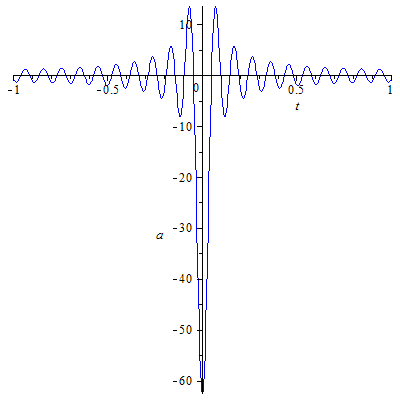
Das ist auch nicht verwunderlich, denn eine "plötzliche Abbremsung" (also ein Sprung der Geschwindigkeit von v auf 0) bedingt eine unendliche Beschleunigung, also eine divergente Reihe für die Beschleunigung. Man muss sich vielmehr wundern, wie Einstein solch ein "spukhaftes Verfahren" vorschlagen konnte. Damit würden die Geschwindigkeit v(t) (rot) und die Beschleunigung a(t) (blau) etwa so aussehen:

|

|

|
|
Für die Darstellung wurde T = 5(passende Einheit) und N = 50 (siehe unten) gewählt. Im Zoom der rechten Spalte sieht man, dass das einer maximalen Frequenz von 10(passende Einheit) entspricht.
Abgesehen davon, dass eine Fourier-Reihe (diskrete Frequenzen) immer einen periodischen Vorgang und nicht eine einmalige Bremsung beschreibt, ist Einsteins Vorschlag in sich widersprüchlich:

Wenn man eine Rechtecksfunktion ("plötzlichen Sprung") durch eine Fourierreihe approximieren will, benötigt man beliebig hohe Frequenzen, was auch durch Einsteins Annahme, dass "Reihenglieder nichts zur Strahlung beitragen", nicht zu beheben ist, wenn man "das beliebige Zeitintervall T" beliebig groß wählt.
Deshalb schreibt Sommerfeld auch:

Man sollte also die 100 Jahre alten "ad hoc Quanten-Postulate", die "kühnen Methoden", die "Verfahren in Ermangelung von etwas Besseren", die "Subtraktionsphysik" und den Quantensprung nicht immer wieder aus der Mottenkiste holen, zumal den großen Geistern schon damals klar war, dass man eine neue Theorie benötigt. Sie hieß damals Wellenmechanik:

In dieser Theorie gibt es keine klassischen Bahnen, sondern nur Zustände, die der deterministischen Schrödingergleichung gehorchen. Im vorliegenden Fall (Bremsstrahlung, kontinuierliches Spektrum) sehen diese Zustände etwa so aus: Bremsstrahlung.
Die Wellenmechanik (oder allgemeiner die Quantentheorie) "stellt diese Zustände gegenüber", d.h., man berechnet durch die Projektion des Anfangszustands auf den Endzustand (Matrixelement) die Wahrscheinlichkeit für einen Übergang, wobei der Ursprung der Strahlung im Dunkeln bleibt! (So gesehen ist also die Quantentheorie eine phänomenologische Theorie ;-).
Im Falle eines diskreten Spektrums sehen die Zustände etwa so aus: " Atombau und Spektrallinien".
In beiden Fällen - kontinuierliches oder diskretes Spektrum - gilt: Die Frequenz der Strahlung ist gleich der Differenzfrequenz der Anfangs- und Endzustände, also der "Frequenzerhaltungssatz". Wenn also der Endzustand die Frequenz 0 hat ("im Unendlichen ruhendes Elektron"), dann hat die Strahlung die maximale Frequenz (oder gesamte Energie) des Anfangszustandes. Interessant dabei ist - sehr verkürzt gesagt -, dass sich die Differenzfrequenz durch die Überlagerung (mathematisch: Betragsquadrat der Summe) der Zustände ergibt und die Übergangswahrscheinlichkeit durch die Projektion (mathematisch: Skalarprodukt).
Aber bis heute
sagt die Quantentheorie nichts über den zeitlichen
(oder gar kausalen)
Ablauf des Übergangs aus und man
lebt mit diesem unbefriedigenden
Zustand, nämlich den "zwei
Dynamiken":
1. Die Zustände (und ihre
Überlagerung) entwickeln sich
deterministisch.
2. Bei einer "Messung", also der
Feststellung, dass ein Übergang
stattgefunden hat,
"kollabieren die Zustände"
- stochastisch.
Wobei die zweite "Dynamik" eigentlich von niemandem ernst genommen wird. Es gibt nicht einmal eine Gleichung dafür und Feynman nennt den "Kollaps" eines Zustandes "a nightmare". In Ermangelung von etwas Besserem postuliert man aber manchmal noch heute, dass die Änderung plötzlich erfolgt: Bohrs Postulate haben wirklich eine spukhafte Fernwirkung über 100 Jahre!
Mit aktuellen Experimenten (2011) ist man allerdings in der Lage, die Bewegung von Elektronen in immer kürzeren Zeitintervallen zu verfolgen. Die Zeitauflösung wird derzeit von Attosekunden auf Zeptosekunden geschraubt. Und bis heute hat noch niemand einen Quantensprung oder einen Kollaps in Null Sekunden beobachtet!
