

Die spektrale Energiedichte der Strahlung eines schwarzen Körpers als Funktion der Frequenz (oder Wellenlänge) mit der Temperatur des Körpers als Parameter.
Da es hier in erster Linie um den Verlauf der Kurven geht, wählen wir "passende Einheiten" (c = k = 1) und vernachlässigen Normierungsfaktoren. Dann lautet die Plancksche Strahlungsformel:
| > | planck:=h*f^3/(exp(h*f/T)-1); |

Darin bedeutet f die Frequenz, T die Temperatur und h das Wirkungsquantum.
Wäre das Wirkungsquantum 0, so ergäbe sich die Strahlungsformel von Rayleigh und Jeans (die für kleine Frequenzen, bzw. h*f << T eine brauchbare Näherung darstellt):
| > | rj:=limit(planck,h=0); |
![]()
Für große Frequenzen (genauer für h*f >> T) erhält man die Wiensche Strahlungsformel:
| > | wien:=h*f^3/(exp(h*f/T)); |

Man beachte: im Vergleich zur Planckschen Strahlungsformel fehlt im Nenner nur " - 1"
Wo liegt das Maximum?
| > | ps:=diff(planck,f); |
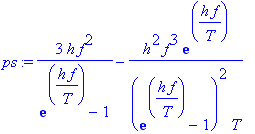
| > | simplify(ps); |

| > | fmax:=solve(ps,f)[1]; |

Passt zum Wienschen Verschiebungsgesetz fmax ~ T.
Zahlenwerte:
| > | h:=1:T:=10: |
| > | evalf(fmax); |
![]()
Und wie sehen die Kurven aus?
| > | plot([planck,rj,wien],f=-1..100,0..2000,color=[red,green,blue]); |
![[Maple Plot]](images/planck11.gif)
Wir vergleichen die Strahlungsformeln für sechs Temperaturen:
| > | display(seq(plot([planck,rj,wien],f=0..120,0..1500,color=[red,green,blue]),T=5..10)); |
![[Maple Plot]](images/planck12.gif)
Planck (rot)
Rayleigh und Jeans (grün, RJ) kann nicht stimmen, weil die Kurven für große Frequenzen gegen Unendlich gehen: Ultraviolettkatastrophe. Jeder noch so kalte Körper müsste Röntgenstrahlen emittieren. Die Annahme von RJ, dass die Wahrscheinlichkeit für die Abstrahlung auf alle Frequenzen gleich verteilt ist, muss also falsch sein.
Wien (blau) sieht im Vergleich zu Planck recht gut aus, aber auch hier gibt es einen Haken:
Für kleine Frequenzen nähert sich die Wiensche Verteilung (blau) einem Grenzwert, der auch bei beliebig hohen Temperaturen nicht überschritten wird, während RJ hier von Planck fast nicht zu unterscheiden ist.
| > | display(seq(plot([planck,rj,wien],f=0..0.1,0..0.1,color=[red,green,blue]),T=1..10)); |
![[Maple Plot]](images/planck13.gif)
Kleine Frequenzen sind aber mindestens so wichtig wie große (Radio, Fernsehen,...): Wäre Wien richtig, so würden Glühlampen keine Wärme abstrahlen (das wäre eine Infrarotkatastrophe - aber nicht für die Hersteller von Glühlampen :-)). Also ist die Wahrscheinlichkeit für die Abstrahlung auch keine Maxwellverteilung (was Wien annahm, um die experimentellen Daten zu fitten).
Die prozentualen Abweichungen (100% entspricht 1 auf der Ordinate) der "alten Strahlungsformeln" von der Planckschen Formel (rot) sehen so aus:

Planck hat also recht genial zwischen der Ultraviolett- und der Infrarotkatastrophe gemittelt...
Und wie kam nun Planck auf seine Verteilung?
Das ist eine längere Geschichte (und Rechnung), die Sie vielleicht demnächst hier lesen können.
Aber die Annahme und das Ergebnis sind bekannt: Die Energie elektromagnetischer Strahlung wird in Quanten emittiert und absorbiert. Und Einstein ergänzte: Elektromagnetische Strahlung ist auch quantisiert unterwegs: Photonen!
Das war der Beginn der Quantenphysik, zu dem auch das Bohrsche Atommodell gehört: Im Atom halten sich die Elektronen nur auf bestimmten Bahnen auf (ohne elektromagnetische Strahlung abzugeben). Der Übergang von einer Bahn zur anderen geschieht im Bohrschen Atommodell mit einem Quantensprung, bei dem ein Photon (elektromagnetische Strahlung) emittiert oder absorbiert wird. Ein Jahrhundert später ist man in der Physik zu einem wesentlich besseren Verständnis der Vorgänge gekommen (-> Quantenelektrodynamik), was aber ewig Gestrige nicht daran hindert, mit Begriffen (oder auch nur Namen), die vor 100 Jahren entstanden, hausieren zu gehen.
Ja - so sieht es im Informationszeitalter aus: Der Quantensprung als Paradebeispiel für Mystifizierung. Wie im finstersten Mittelalter (Strahlung schwarzer Körper?)...
Etwas leichter verdaulichere Kost: Wir sehen uns die Strahlungsformeln noch einmal als Funktion der Wellenlänge an
| > | planck:=h/lambda^5/(exp(h/(lambda*T))-1); |

| > | rj:=limit(planck,h=0); |
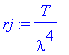
| > | wien:=h/lambda^5/(exp(h/(lambda*T))); |

| > | display(seq(plot([planck,rj,wien],lambda=0..0.1,0..3e6,color=[red,green,blue]),T=5..10)); |
![[Maple Plot]](images/planck33.gif)
| > | display(seq(plot([planck,rj,wien],lambda=2..4,0..0.2,color=[red,green,blue]),T=5..10)); |
![[Maple Plot]](images/planck34.gif)
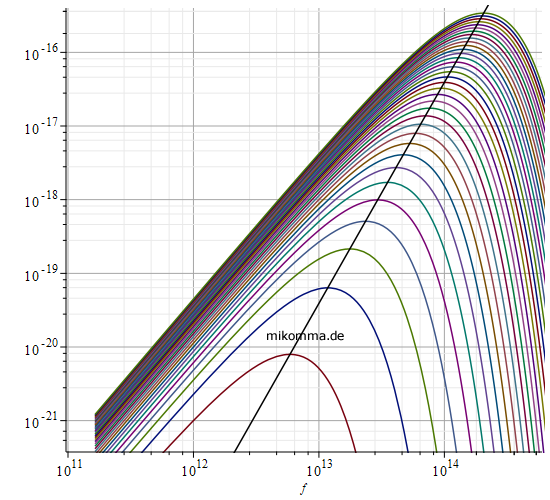
Auf vielfachen Wunsch hier noch ein paar Diagramme zu Plancks Formel (https://doi.org/10.1002/andp.19013090310 S. 561, Gl. (12))

in MKS-Einheiten. Die spektrale Energiedichte u(f,T) hat als Funktion der Frequenz f die Einheit von "Energie pro Volumen und Frequenz" (oder Wirkung pro Volumen), also 1Js/m3. Ortskurve der Maxima in schwarz.
T = 500-2500K, in Schritten von 100K

T = 50-1000K, in Schritten von 50K

T = 100-3500K, in Schritten von 100K , doppelt logarithmisch
Spektrale Energiedichte als Funktion der Wellenlänge λ
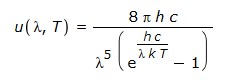
in MKS-Einheiten von "Energie pro Volumen und Länge", also 1J/m4. Ortskurve der Maxima in schwarz.
T = 500-2500K, in Schritten von 100K

T = 50-1000K, in Schritten von 50K

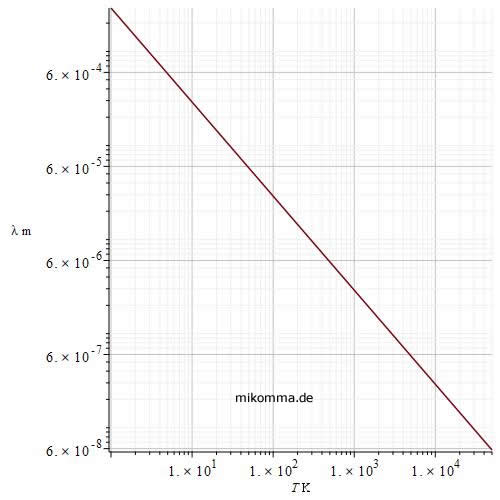
T = 100-3500K, in Schritten von 100K , doppelt logarithmisch

Manchmal möchte man auch wissen, bei welcher Frequenz bzw. Wellenlänge das Spektrum des schwarzen Körpers sein Maximum bei einer bestimmten Temperatur hat (Wiensches Verschiebungsgesetz):

Siehe auch: Spontane Emission, logistisch | Weisskopf-Wigner | Ensemble-Individuum | atomarer Dipol
komma_AT_oe.uni-tuebingen.de
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top