

Über die spontane Emission von Photonen
Spontaneous photon emission revisited (Google-translation)
Dieser Artikel soll die seit 1930 gängige Praxis, den
Elementarprozess der Emission eines Photons in atomaren Übergängen
phänomenologisch mit dem radioaktiven Zerfall (von Kernen) gleichzusetzen, etwas
näher beleuchten. Die Standardbehandlung dieses Themas geht zurück auf Weisskopf
und Wigner:
V. Weisskopf und E. Wigner, ZS. f. Phys. 63, 54, 1930, "Berechnung der natürlichen Linienbreite auf Grund der Diracschen
Lichttheorie".
Für
die emittierte Strahlung verwendet man in diesem "Standardmodell" die Analogie
zum gedämpften harmonischen Oszillator, siehe
S. Kikuchi, Zeitschrift für Physik, July 1930, Volume 66, Issue 7–8, pp 558–571,
"Über die Fortpflanzung von Lichtwellen in der Heisenberg-Paulischen Formulierung der Quantenelektrodynamik",
die ja gut zum "exponentiellen Zerfall" passt. Zitat Kikuchi S. 569:

Demnach hat man sich ein Photon etwa so vorzustellen (Amplitude der Feldstärke):
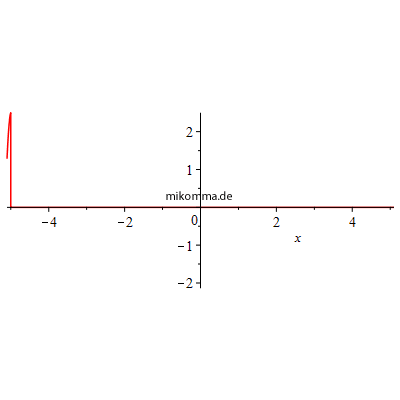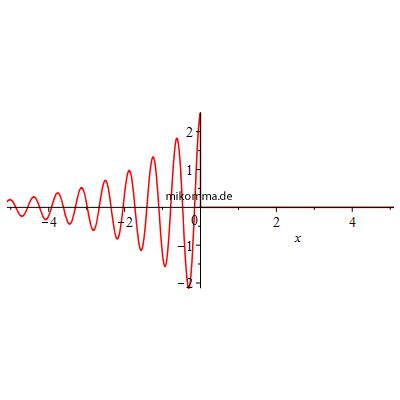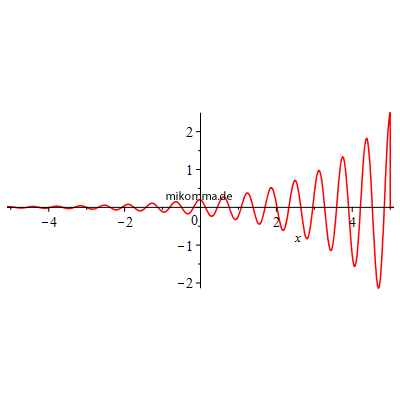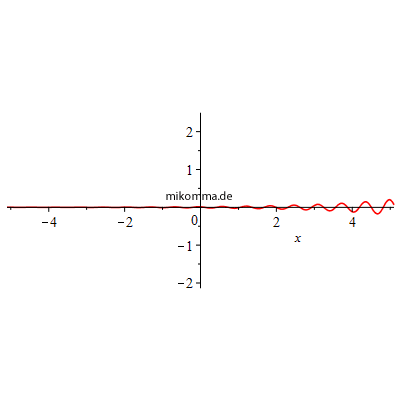 |
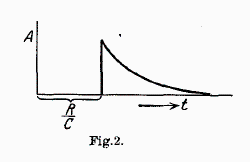
Aber auch
wenn man sich um
Kausalitätsprobleme nicht
kümmert, bleibt ein Denkfehler:
der "exponentielle Zerfall" des
angeregten Zustands wird auf die
"Amplitude des Photons"
übertragen. Dieser Denkfehler wird seit 1930
nahtlos übernommen, z.B.
M.O. Scully, M.S. Zubairy
"Quantum Optics" S. 208-9: Das klappt aber nur, wenn vor der Zeit 0 der angeregte Zustand nicht besetzt war: "Abschneide-Physik"! Eine Liste von Zitaten der in sich widersprüchlichen oder zirkulären Argumentationen zu diesem Thema wäre relativ lang... :)
|
| Das Atom sendet also wie ein Funkeninduktor? Nein - mit diesem Modell kann etwas nicht stimmen! Selbst bei einem klassischen Funkeninduktor kann die Feldstärke nicht von 0 auf einen endlichen Wert springen (die klassische Elektrodynamik ist kausal), und auch die QED kann solche Singularitäten nur durch "Renormierungen" beheben. |
Die Vorstellung eines Photons, dessen Feldstärke (Amplitude) "zur Zeit 0" schlagartig von 0 auf den maximalen Wert springt, ist also etwas problematisch, ganz abgesehen davon, dass man keine Wellenfunktion für ein Photon angeben kann (sondern nur "a kind of wave function for a photon" :). Aber auch wenn man die spontane Emission eines Photons einfach als einen völlig unbestimmten "Emissionsakt" in das Reich der Unbeobachtbarkeit schiebt, bleiben einige Probleme im "Standardmodell der spontanen Emission":
Weisskopf-Wigner-Näherung (WeWi):
Abgesehen von Näherungen, die gemacht werden, um die "Bewegungsgleichungen" (Mastergleichungen), die aus der SGL für die W-Amplituden der Zustände folgen, lösen zu können, wird die Lösung nicht wirklich berechnet, sondern vorausgesetzt: "Das Atom folgt bei der Emission von Photonen dem radioaktiven Zerfallsgesetz".
Dabei geht es in WeWi nicht nur um einen (einzigen) Übergang von A nach B, sondern insbes. auch um Zerfallsreihen (WeWi S. 69):

Die Gleichungen für den radioaktiven Zerfall werden also 1:1 auf die Zustände eines Atoms übertragen, das durch die spontane Emission von Photonen von a nach b nach c... übergeht.
Hier ist ein Beispiel mit 4
radioaktiven Elementen (drei Übergängen): 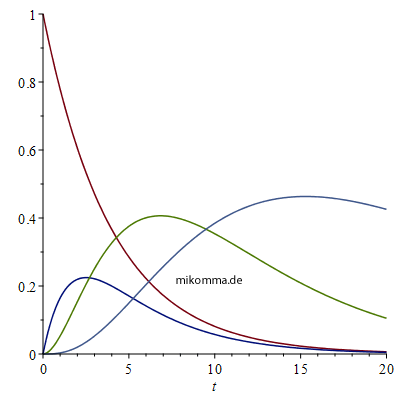 |
Und hier ein Beispiel mit zwei Übergängen (drei Kurven unten) bzw. zwei Photonen (zwei Kurven oben): 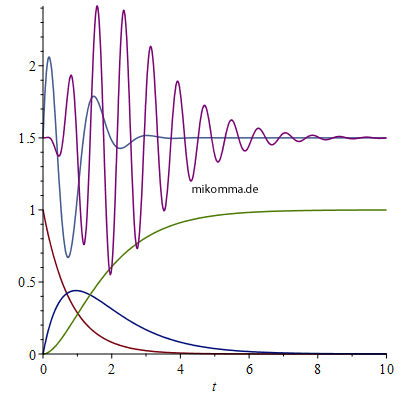 |
| Instabile Tochterelemente erreichen nie die volle "Besetzungszahl". Erst durch Hinzufügen des "Grundzustands" (hier nicht dargestellt) wird die Summe aller Kurven 1. Übertragen auf den "Zerfall eines Atoms" bedeutet das, dass sich das Elektron auf seinem Weg in den Grundzustand nie vollständig in einem der Zwischenzustände befindet. Übrigens würde das bedeuten, dass ein Atom auf seinem Weg zum Grundzustand (der sicher eine endliche Zeit dauert) alle "erlaubten Frequenzen" mehr oder weniger gleichzeitig abstrahlt (siehe Photokaskade). Das kann durchaus richtig sein, widerspricht aber der Annahme "zur Zeit t = 0 " (oder wann auch immer) "springt das Atom" oder findet der "Emissionsakt" statt. | Hier ist nun die Besetzung des Grundzustands mit eingezeichnet (grün). Für die "Amplitude der Photonen" wurde als Einhüllende das Produkt der Besetzungszahlen (das zeitabhängige Dipolmoment, siehe) genommen. Die kleine Frequenz gehört zum ersten Übergang und die größere Frequenz zum zweiten. Folgt man der Argumentation von WeWi und Kikuchi, so müsste die Emission beider Photonen schlagartig "zur Zeit 0" beginnen. Man liest aber bei WeWi (z.B. S.58): "...und die Wahrscheinlichkeit, dass ein Atom, das vor langer Zeit im Zustand A war, nacheinander drei Lichtquanten mit den Frequenzen ... emittiert". |
Der WeWi-Ansatz impliziert auch, dass das Atom zur "Zeit t = 0" mit maximaler Leistung zu strahlen beginnt, bzw. dass die Absorption mit maximaler Leistung zur "Zeit t = 0" endet, also entweder ein Sprung oder ein Knick vorliegt. Zur Rechtfertigung dieses Modells wird auf die Analogie zum gedämpften harmonischen Oszillator (mechanisch oder elektrisch) verwiesen, der zur Zeit t = 0 "eingeschaltet wird". Nun kann man aber Atome
1. nicht zur Zeit t = 0 "ein- oder ausschalten", sondern höchstens bis zur Zeit t = 0 im angeregten Zustand halten, und dann die externe Quelle/Anregung abschalten, und
2. reagiert ein Atom nicht wie eine gespannte Feder, die beim Loslassen mit der Frequenz des "angeregten Zustands" schwingt, sondern die Strahlung entsteht durch Überlagerung zweier Zustände mit der Schwebungsfrequenz. Wenn also das Atom zur Zeit t = 0 im stationären angeregten Zustand ist, kann es nicht strahlen. Vielmehr muss sich erst ein Dipolmoment (oder allgemeiner ein Multipolmoment) ausbilden, das erst dann maximal wird, wenn beide Zustände gleiches Gewicht haben.
3. Sei noch angemerkt, dass die Übertragung des Modells "radioaktiver Zerfall" (gültig für ein Ensemble) auf das zeitliche Verhalten eines einzelnen Atoms bei der Emission oder Absorption eines Photons (also den Elementarprozess) rein phänomenologisch und nicht zwingend logisch ist. Das "exponentielle Zerfallsgesetz" gilt immer, wenn alle Elementarprozesse die gleiche Wahrscheinlichkeit (Zerfallsrate) haben. Daraus kann man aber nicht schließen, dass die Elementarprozesse selbst "exponentiell abklingen", und die emittierte Strahlung ein Lorentz-Spektrum (= natürliche Linienform) aufweist: Aus einer Bilanz (oder aus Mittelwerten) lässt sich eine Dynamik des Elementarprozesses nicht zwingend ableiten.
Neues Modell - logistisches Modell
Anstatt phänomenologisch von einem exponentiellen Zerfall des Atoms auszugehen, und diesen auf das Photon zu übertragen, wird die Dynamik der Dipolschwingung in den Vordergrund gestellt. Dies führt auf die (nichtlinearen) Differentialgleichungen für logistisches Wachstum (s.u. Theorie), die für mehr als einen Übergang leider nur numerisch lösbar sind.
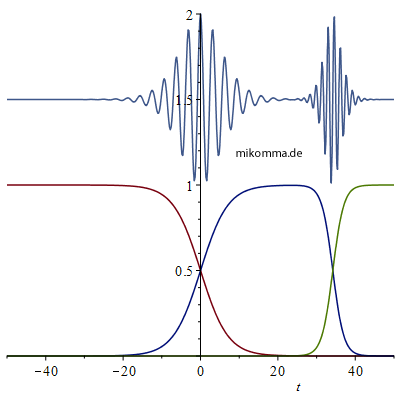 |
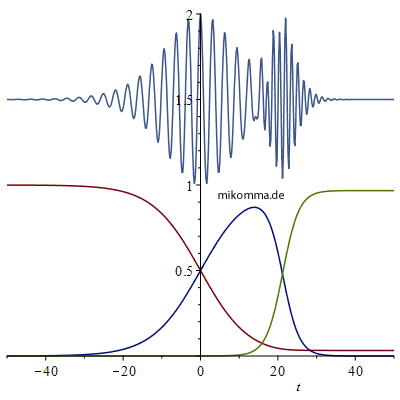 |
Über den Kurven für die Besetzungszahlen sind wieder "die Amplituden der Photonen" dargestellt. Im Gegensatz zum "Standardmodell des exponentiellen Zerfalls" haben die Zustände des Atoms (A (rot), B (blau) und C (grün)) nun auch eine Vergangenheit (t < 0) und dementsprechend erscheinen die Photonen als Wellenpakete ohne "scharfe Kante".
Ein wichtiges Merkmal des "logistischen Modells" sind die Anfangswerte: In der linken Abbildung ist C(0)=10-10 und in der rechten Abbildung C(0)=10-3 (zusätzlich wurden in der rechten Abbildung die "Zerfallsraten" verringert). D.h., im logistischen Modell gibt es keine stationären Zustände. Auch für C(0)=10-1000 würde ein Übergang "irgendwann" (das lässt sich auch berechnen :) stattfinden, quasi spontan und ohne Unterstützung durch das Vakuum. Aber weil das System sehr empfindlich auf Störungen reagiert, kann selbst das Vakuum einen Übergang auslösen - und erst recht die allgegenwärtige Hintergrundstrahlung bei Temperaturen über dem absoluten Nullpunkt (wobei dann beide "Triggermechanismen" für die Impulserhaltung sorgen).
Ein zweites Merkmal des logistischen Modells ist die "Trennung der Emissionsakte" (wie von WeWi stillschweigend angenommen, aber nicht erfüllt). Wenn der Grundzustand C "zur Zeit 0" nicht besetzt ist, und der Übergang von A nach B "schnell genug" erfolgt (linke Abbildung), werden die Photonen nacheinander emittiert. Andererseits bewirkt eine "zu frühe Bevölkerung von C" (oder ein "zu langsamer" Übergang von A nach B) eine zeitliche Überlappung der Photonen, bzw. eine "Niveau-Unschärfe" (Linienverbreiterung) des ersten Übergangs - ganz im Sinne von WeWi.
Das logistische Modell erklärt also den Quantensprung? Spaß beiseite, hier kommt noch etwas Theorie...
Ausgangspunkt ist wie in Emission eines Photons wieder der Zustand
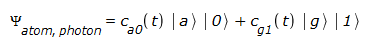
Wie oben erwähnt, geht das hier vorgeschlagene logistische Modell
der spontanen Emission davon aus, dass
die von einem Atom abgestrahlte Leistung proportional zum Quadrat des Dipolmoments
ist, dessen Zeitabhängigkeit durch ![]() gegeben ist (in diesem Zusammenhang können die c als reell betrachtet werden).
gegeben ist (in diesem Zusammenhang können die c als reell betrachtet werden).
Der Sachverhalt lässt
sich kompakter formulieren, wenn man von den W-Amplituden c zu ihren
Quadraten übergeht, bzw. zur Dichtematrix ρ ("optische Blochgleichungen").
Für zwei Zustände (einen Übergang) lassen sich die Differentialgleichungen
(Mastergleichungen) exakt lösen.
|
Die Änderung des Grundzustands ρgg ist dem Quadrat des Dipolmoments ρgg(1-ρgg) (= abgestrahlte Leistung) proportional. Stellt man diesen physikalischen Sachverhalt in den Vordergrund und gibt nicht ein "exponentielles Abklingen" als Lösung vor, so erhält man mit der Proportionalitätskonstanten k die Differentialgleichung:
auch bekannt als die logistische Differentialgleichung. Sie hat die "standartisierte" Lösung (ρgg(0)=1/2):
auch bekannt als logistische Funktion, oder kumulative logistische Verteilung (bzw. Fermi-Dirac-Verteilung - an der Hochachse gespiegelt).
Mit der Ableitung (= vom Dipol abgestrahlte Leistung):
|
Grundzustand ρgg (rot) und Ableitung von ρgg nach der Zeit (grün):
|
|
Das Frequenzspektrum erhält man durch Fouriertransformation. Die Amplitude der E-Feldstärke ist proportional zur Wurzel der Energie (od. Leistung):
Auch bekannt als hyperbolic secant distribution. Weil das Frequenzspektrum ohnehin auf 1 (Fläche) normiert werden muss, wurde in obiger Proportionalität k vernachlässigt und nur die Abhängigkeit der elektrische Feldstärke von t betrachtet.
Die Fouriertransformierte von E(t) ist dann
und ihr auf 1 normiertes Quadrat, also das Intensitätsspektrum für ein Photon mit der Energie 1 (= ℏω)
|
Vergleich von Lorentz- (rot), Logistik- (blau) und Gaußlinie (grün) mit gleicher fwhm (alle Verteilungen auf 1 normiert).
|
| Bei diesem Vergleich (obige Abbildung) kommt es zunächst auf die Form der Linien an: Die Lotentzlinie hat immer die weitesten "Flügel", weil das (künstliche) Abschneiden des zeitlichen Verlaufs der Emission einen hohen Anteil beliebig hoher Frequenzen bedingt. Interessant ist auch, dass sich die Gaußlinie nur wenig von der Logistiklinie unterscheidet, und beide Linientypen "ihre eigenen Transformierten" sind (Gauß - Gauß und sech - sech). |
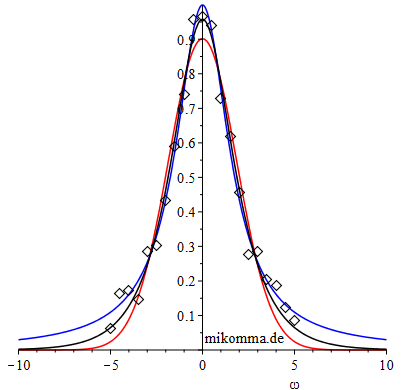
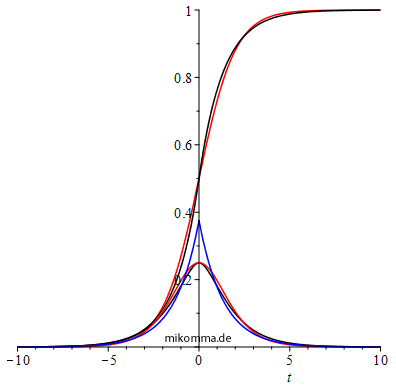
| Es ist übrigens gar nicht so einfach, aus Messdaten die Linienform zu bestimmen. In der Abbildung unten wurden aus einer Lorentzverteilung mit Maximalwert 1 "Messpunkte" erzeugt, indem zur Ordinate der Verteilung Zufallszahlen zwischen -0.05 und +0.05 addiert wurden. Die drei Kurven zeigen Kurvenfits für die Modelle Lorentz (blau), Gauß (rot) und Logistik (schwarz). | Eine Möglichkeit, die Abschneidephysik zu reparieren, wäre eine "Zerfallskurve", die durch die Spiegelung des abgeschnittenen exponentiellen Zerfalls am Punkt (0 | 0.5) ergänzt wird. Bei passender Wahl der Parameter unterscheidet sich dann die zugehörige Kurve für ρgg (schwarz) nur minimal von der logistischen Funktion (rot). Das Gleiche gilt für die Produkte ρgg(1 - ρgg ), die ebenfalls unten schwarz und rot dargestellt sind ("Glockenkurven"). Allerdings hat dann die Ableitung der zusammengesetzten Funktion (schwarz) einen Knick (blau), bzw. "die Amplitude des Photons" hat in der Mitte eine Spitze (einen Quantenknick :), während die Ableitung der logistischen Funktion dem Produkt ρgg(1 - ρgg ) proportional ist. Das ist aber immer noch besser, als ein "Sägezahnphoton", das "zur Zeit 0" beginnt... |
 |
 |
| Und wie sieht nun das Photon aus? | |
|
Nebenstehend noch eine Animation zur
Verdeutlichung des Unterschieds zwischen einem
"Kikuchi-Photon"
(navy, sprunghafter Beginn bei t = 0 mit
exponentiellem Abklingen) und einem
"logistischen Photon" (purple, secans
hyperbolicus). Dargestellt sind die Einhüllenden
der (momentanen) Energie, jeweils normiert auf
die Fläche 1 und mit der "Zerfallskonstanten"
als Parameter. Heisenberg war ja Zeit seines
Lebens davon überzeugt, dass die Diskontinuität
ein "Wesensmerkmal der Quantenmechanik" sei.
Sein Schüler Kikuchi hat diese Überzeugung
zumindest zu einer Hälfte übernommen: "Die
Emission eines Photons setzt schlagartig ein"
(natürlich zur Zeit t = 0!), aber danach (für t
> 0) sind wir wieder in der klassischen Physik,
und alles verläuft kontinuierlich - alles bis
ins Detail durchgerechnet mit den
Maxwellgleichungen! Aber zum Glück gibt es ja die Heisenbergsche Unschärferelation und die Fouriertransformation! Die zugehörigen Linienprofile sind bei t = 10 (t in diesem Fall als Frequenz) zu sehen. Lorentzprofil breit (hellblau), "logistisches Profil" schmal (hellgrün). Die Darstellung wurde nach oben abgeschnitten - wegen der Unschärferelation ΔfΔt = const :-). (Zur Orientierung: die Maxima der Kurven liegen oberhalb von 3.) |
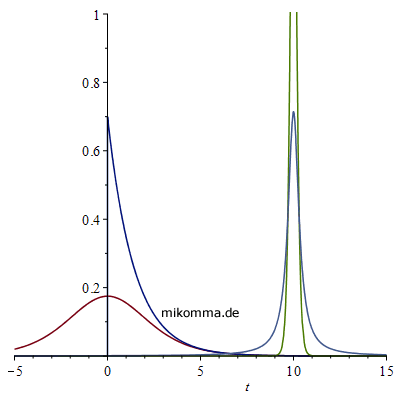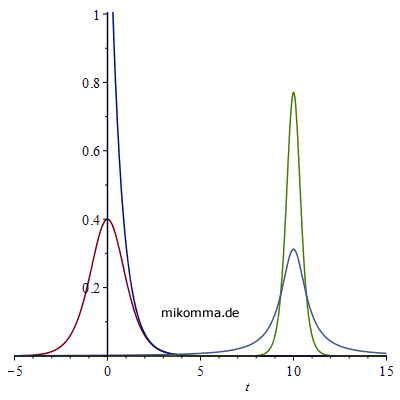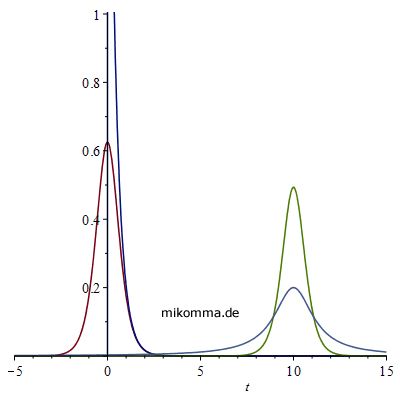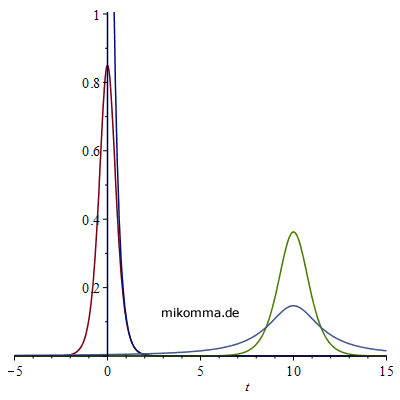 |
|
Die nächsten beiden Animationen zeigen das "Kikuchi-Photon" (blau) und das "logistische Photon" (rot). Links die Amplitude und rechts die Energie (Quadrat der Amplitude, gesamte Energie jeweils auf 1 norniert). |
|
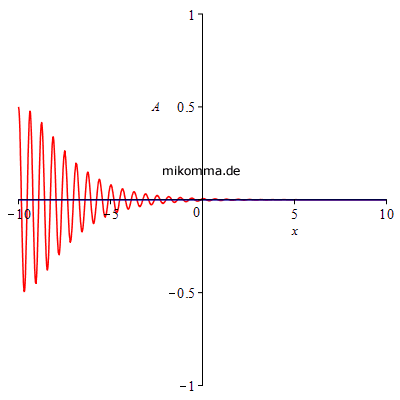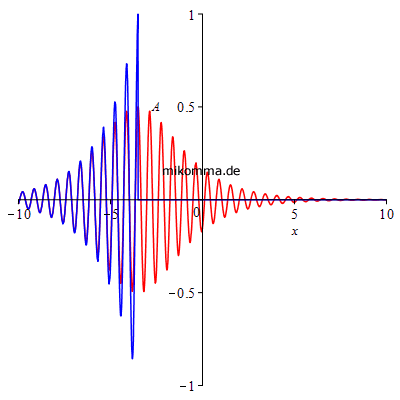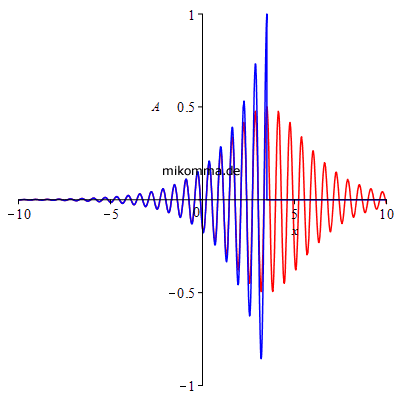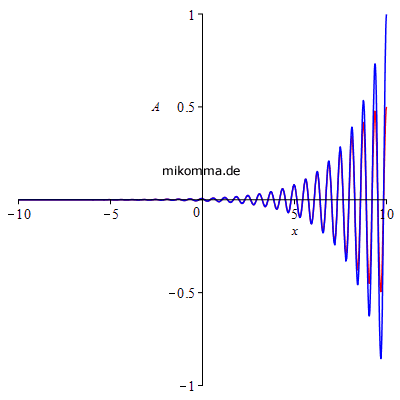 |
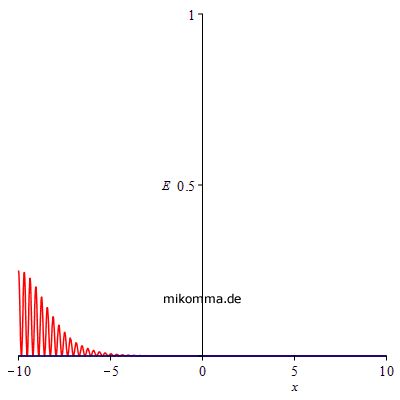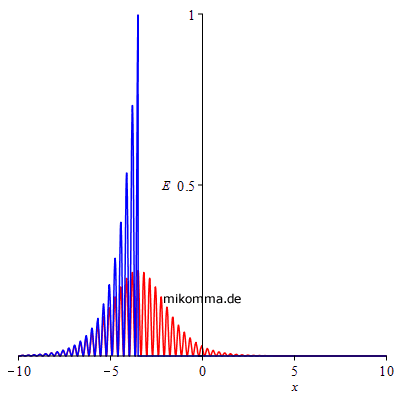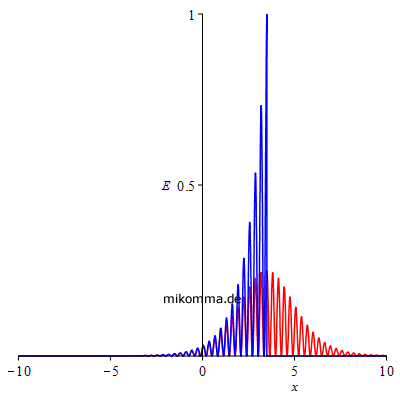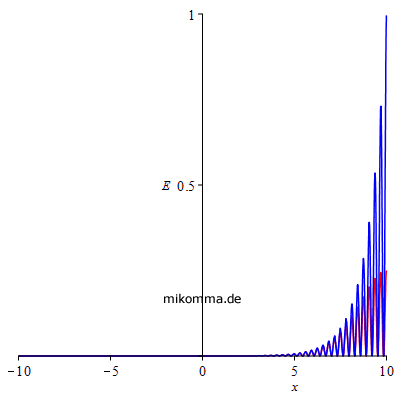 |
Man könnte also "Kikuchi-Photonen" auch als "halbe Photonen" bezeichnen, aber die gibt es ja bekanntlich nicht :-).
Und wenn nun beim "Zerfall eines Atoms" mehr als ein Photon emittiert wird? Dann sagt die WeWi-Theorie voraus, dass dies wie beim radioaktiven Zerfall geschieht, also simultan auf allen möglichen Frequenzen/Übergängen, im Widerspruch zu der von WeWi selbst gemachten Annahme, dass die Übergänge (= Quantensprünge) nacheinander stattfinden (siehe auch die bedingten Wahrscheinlichkeiten der Monte-Carlo-Quantenspringer :-). Was sagt das "logistische Modell" dazu?
|
Kaskaden im logistischen Modell Der zeitliche Verlauf einer Kaskade von n = 4 nach 3, 2, 1 könnte z.B. so aussehen (Abbildung rechts). Die rote Kurve zeigt die Niveaus im Abstand der Hauptquantenzahlen (~1/n2), die blaue Kurve die Abstrahlung, modelliert als zeitliche Änderung der Energie des Atoms. Im Gegensatz zum "Standardmodell" (WeWi) muss sich im logistischen Modell das Atom bei der sukzessiven Emission von Photonen nicht an eine "radioaktive Zerfallsreihe" halten, die einerseits durch Differentialgleichungen beschrieben wird, und andererseits "zufällige Emissionsakte" (Quantensprünge) zu beliebiger Zeit erfordert, was ja schon in sich widersprüchlich ist: Im logistischen Modell laufen die Übergänge kontinuierlich ab, wobei die Geschwindigkeit des Übergangs (= Steigung der roten Kurve an den Übergängen) wie oben berechnet wurde. Wann ein Übergang stattfindet, bzw. in welchem zeitlichen Abstand die Übergänge erfolgen, hängt im logistischen Modell von den "Anfangsbedingungen" ab: Die "horizontalen Kurvenstücke" der roten Kurve sind nicht exakt horizontal, sondern haben (in nebenstehender Darstellung) eine Steigung von der Größenordnung 10-10. Schmetterlingseffekt! (Und wem dieser Zufall nicht objektiv genug ist, kann gerne noch das QED-Vakuum als Auslöser und zur Impulserhaltung einbeziehen :-). |
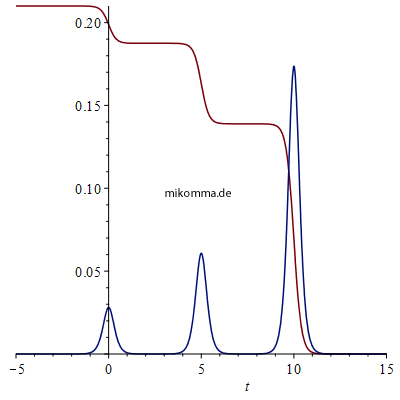 |
Zum Schluss noch die Visualisierung der atomaren Wellenfunktionen zweier Kaskadenübergänge im Vergleich. Links das logistische Modell, rechts das Standardmodell der Photonenkaskade.
n = 4 -> 3-> 2, maximales l, m = 0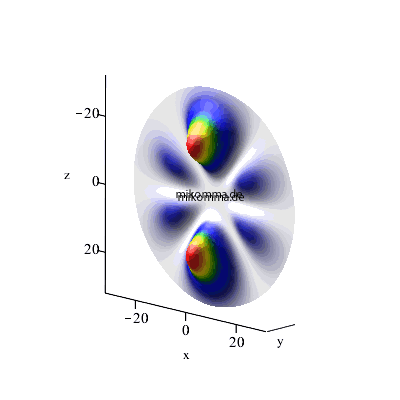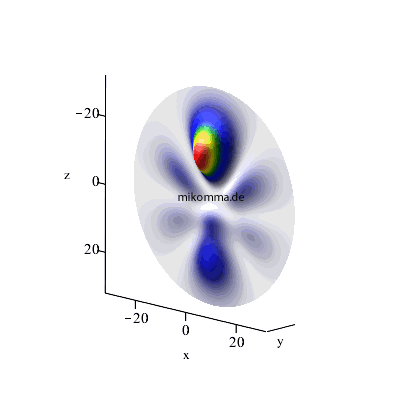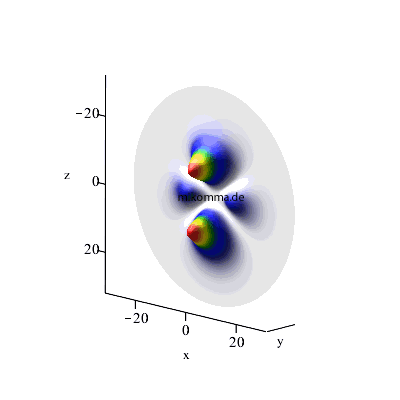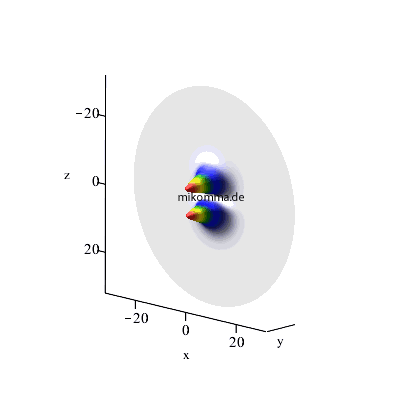 |
n = 4 -> 3-> 2, maximales l,
m = 0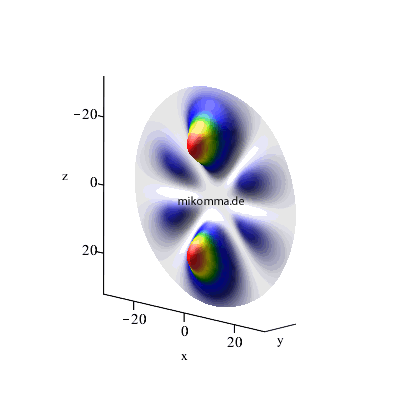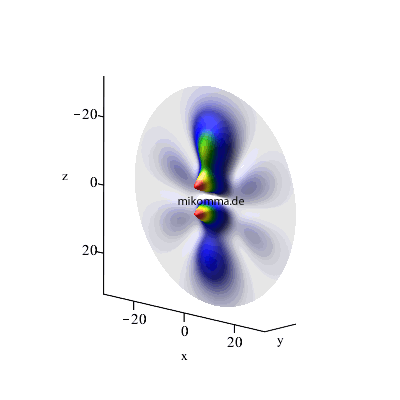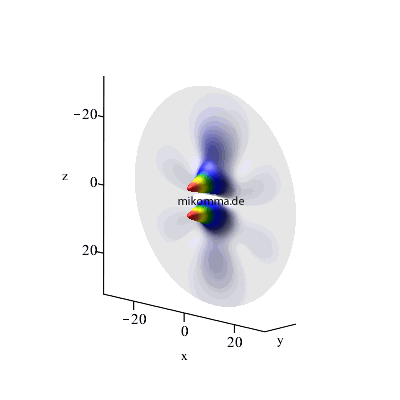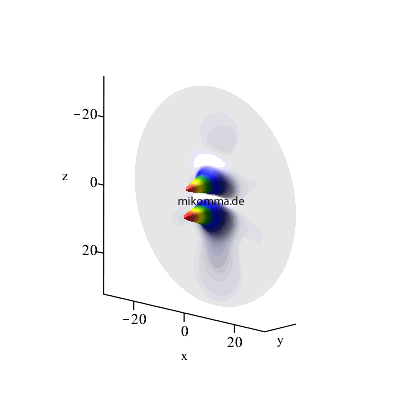 |
n = 7 -> 6 -> 5, maximales m und l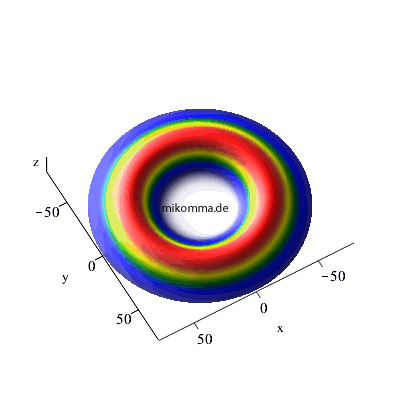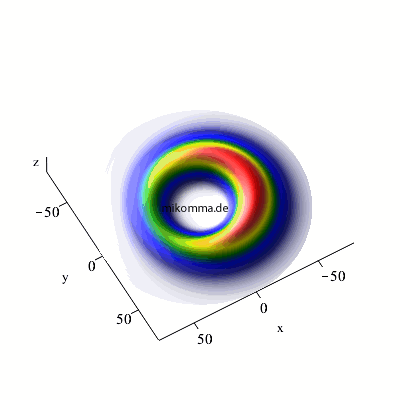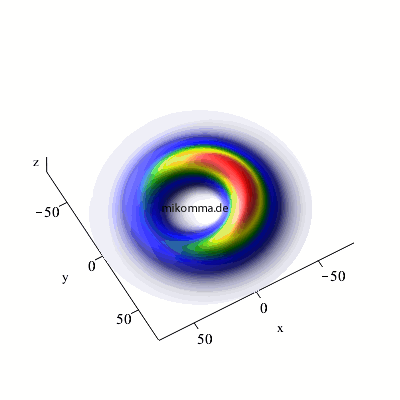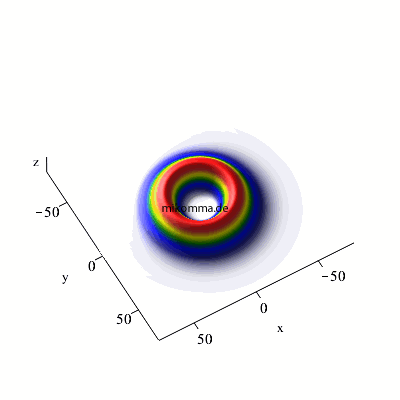 |
n = 7 -> 6 -> 5, maximales m
und l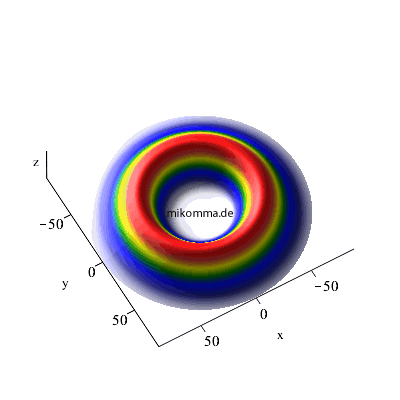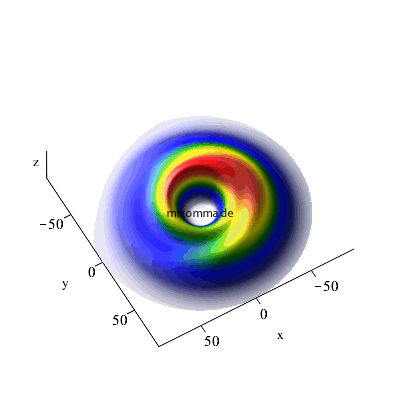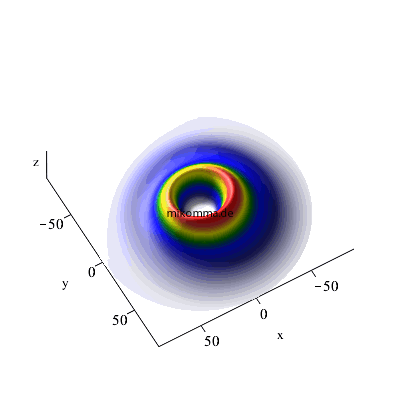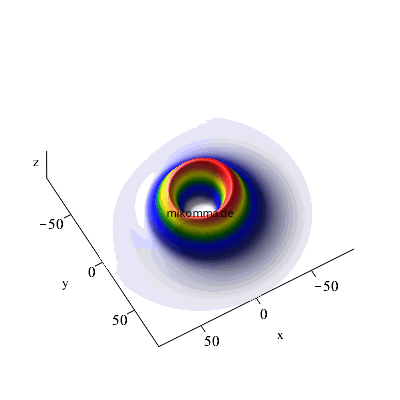 |
| In beiden Fällen sieht man auch in der Darstellung der Wellenfunktionen deutlich, dass der Zwischenzustand (n = 3, bzw. n = 6) im Standardmodell nur andeutungsweise vorkommt. |
Zusammenfassung und Ausblick
Wenn man die Näherung von Weisskopf und Wigner genauer betrachtet, stellt man
fest, dass es gar nicht nötig gewesen wäre, ein exponentielles Abklingen des
angeregten Zustands vorauszusetzen. Vielmehr ergibt sich das exponentielle
Abklingen aus den dort gemachten Näherungen und der Linearität der
Schrödingergleichung, bzw. der Linearität der aus der SGL folgenden
Mastergleichungen.
Es bleibt allerdings erstaunlich, dass der Elementarprozess, bzw. die
Dynamik der
spontanen Emission eines Photons seither kaum hinterfragt wurde, abgesehen von
wenigen Ausnahmen wie z.B. P.W. Milonni (s.u.). Man gibt sich eben gerne mit der
ersten Näherung (Linearität) zufrieden, so lange dieses Standardschema (Lorentzlinie)
passt, und Messungen kein Indiz für die Notwendigkeit einer Korrektur des
Standardmodells liefern. Aber welche Messungen und welche Auswertungen? Wenn von
vornherein "klar ist", dass die "natürliche Linienbreite" und insbes. Linienform
durch das "exponentielle Zerfallsgesetz" gegeben sind, macht man keine
Experimente, die das widerlegen könnten, und alle Kurvenfits werden so
eingerichtet, dass die Kurven zum Standardmodell - der Lorentzlinie - passen.
Darüber hinaus kann die "natürliche Linienbreite" experimentell nur in den
seltensten Fällen gemessen werden (wenn überhaupt!), weil die Messungen durch
Stoßverbreiterung (Lorentzspektrum) und Dopplerverbreiterung (Gaußspektrum)
überlagert werden, die die Charakteristika des Elementarprozesses um mehrere
Größenordnungen übersteigen. Man kümmert sich deshalb in der Praxis eher darum,
die Messergebnisse zu entfalten (Voigt-Profile), und weniger um den
Elementarprozess an sich, dessen Linienbreite oft als nicht messbar angesehen
wird. Dann fällt es natürlich nicht auf, wenn der Elementarprozess eine kleinere
Linienbreite und insbesondere eine schmalere Linienform hat als die
standardmäßig vorausgesetzte Lorentzlinie.
Das hier vorgestellte "logistische Modell der spontanen Emission" fiel also über
lange Zeit durch das Raster, weil
a) der Elementarprozess der spontanen Emission mit dem Verhalten eines
Ensembles, das der linearen SGL "gehorcht", gleichgesetzt wurde, und
b) Linienbreite und -form des Elementarprozesses unterhalb der "nicht messbaren"
Werte liegen, wenn der Elementarprozess nicht linear ist.
Was nun? Es fehlt ein experimentum crucis! Man könnte z.B. untersuchen:
1. Superradianz: Wenn Licht im Medium Solitonen bilden kann, die
o.g. Gleichungen folgen, dann sollte es auch möglich
sein, das Medium so weit zu verdünnen, dass man den Elementarprozess sieht?
2. Rydbergatome: Man hat inzwischen gelernt, Atome so zu manipulieren, dass sie
sich quasi klassisch verhalten. Dann müsste man doch auch herausfinden können,
ob in einer atomaren Kaskade die Photonen "gleichzeitig" oder nacheinander
emittiert werden?
Literatur:
- V. Weisskopf und E. Wigner, ZS. f. Phys. 63, 54, 1930
Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie.
- S. Kikuchi, Zeitschrift für Physik, July 1930, Volume 66, Issue 7–8, pp
558–571
Über die Fortpflanzung von Lichtwellen in der Heisenberg-Paulischen Formulierung
der Quantenelektrodynamik.
- P. W. Milonni, Am. J. Phys., Vol. 52, No. 4, April 1984
Why spontaneous emission?
© Juli 2017, Dr. Michael Komma (VGWORT)
Anmerkung: In dem Anfang Juni 2019 veröffentlichten Artikel "To catch and reverse a quantum jump mid-flight", wird experimentell nachgewiesen, dass ein atomarer Übergang kontinuierlich und deterministisch abläuft (zumindest in einem künstlichen Atom). Die theoretische Behandlung erfolgt mit "Quantentrajektorien" und führt im Endeffekt auf das gleiche Ergebnis wie im Logistischen Modell vorgeschlagen.
Aus aktuellem Anlass (März 2020): Die mathematische Beschreibung atomarer Übergänge (Systeme mit zwei Zuständen) verwendet Systeme von Differentialgleichungen, die eng verwandt sind mit "dynamischen Systemen", z.B. SIR-Modell in Corona-Zeiten.
Siehe auch:
Emission eines Photons | Galerie | Kaskade | Weisskopf-Wigner | Ensemble-Individuum | Minev Quantum Jump | Superradianz | Atomarer Dipol
Historisches zum Quantensprung
H-Orbitals aus ' Moderne Physik mit Maple'
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top