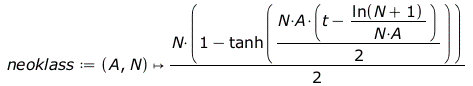|
Superradianz Eine kurze Notiz 1. Neoklassisch Wie in Über die spontane Emission von Photonen ausgeführt, kann die Emission eines Photons, also der Übergang eines einzelnen Atoms von einem höheren zu einem niedrigeren Energienivau, durch die logistische Gleichung beschrieben werden:
Leider sind einzelne Atome und ihre Zustände und Übergänge nicht ganz einfach zu beobachten. Wie wäre es mit einem "makroskopischen Atom", also einer "geeigneten Ansammlung von N identischen Atomen"? Dann müsste man - rein theoretisch - in obiger Gleichung für ρgg nur die 1 durch N ersetzen. Die logistische Gleichung lautet dann
Zum Vergleich mit der quantenoptischen Beschreibung (s.u.) wurden die Bezeichnungen (und das Vorzeichen) an die Notation von Mandel und Wolf [MaWo] angepasst. Diese DG hat die allgemeine Lösung
bzw. mit t0 als zeitliche Verschiebung
was sich auch als tanh-Funktion schreiben lässt
Im Vergleich zur standardisierten Lösung ändert sich also nicht nur die Amplitude, sondern auch die Proportionalitätskonstante im Exponenten um den Faktor N. Für die abgestrahlte Leistung gilt dann
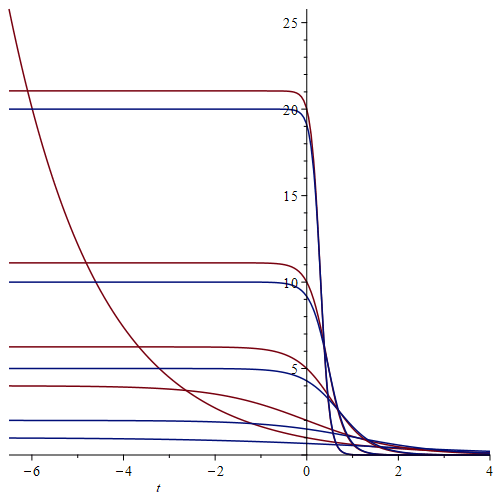
was sich auch wie oben als sech2-Funktion schreiben lässt. Hier ist eine Veranschaulichung für k=0.5, t0=2 und N=2,5,10 (rot: Zustand, blau: Strahlung):
Allein aus dieser "neoklassischen" Behandlung ergibt sich also, dass die abgestrahlte Leistung mit N2 wächst, und die volle Halbwertsbreite des Pulses proportional zu 1/Nk ist, was als charakteristisches Merkmal für Superradianz gilt.
2. Quantenoptische Beschreibung In "Optical Coherence and Quantum Optics", L. Mandel and E. Wolf, S. 844 (16.6-14) [MaWo] findet man die Differentialgleichung
Darin ist y(t) = |c2(t)|2 die Dichte des angeregten Zustands, N die Anzahl Atome und A der "Einsteinkoeffizient". Diese DG hat die allgemeine Lösung
Damit wird allerdings die Dichte des angeregten Zustands für negative Zeiten größer als 1
und für ein einzelnes Atom unendlich. Aber das lässt sich ja beheben, wenn man wie [MaWo] nur positive Zeiten betrachtet, und die Dichte zur Zeit 0 auf 1 setzt:
Damit sehen die Lösungskurven für N=1..10 so aus
3. Vergleich Neoklassik - Quantenoptik Obige quantenoptische Lösung (11) bezieht sich auf ein Atom. Zum Vergleich mit der neoklassischen Lösung muss sie mit der Zahl N der Atome multipliziert werden:
Mit
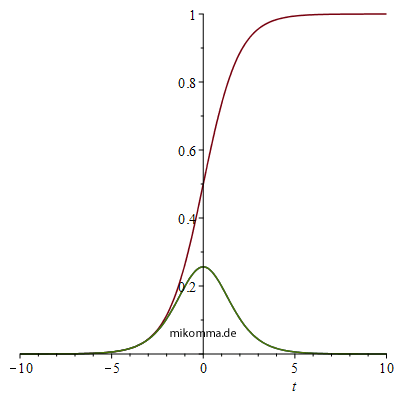
erhält man dann (rot: "quantenoptisch", blau: "neoklassisch")
Wobei die rechte Abbildung das Verhalten der Lösungen für t<0 verdeutlicht. D.h., ein einzelnes Atom "zerfällt" exponentiell, aber sobald nur ein zweites Atom hinzukommt, "zerfallen" beide logistisch. Das liegt natürlich am gemachten Ansatz. Der Zustand des "N-Atome Systems" wird als ein Produktzustand von Überlagerungszuständen angesetzt ([MaWo] S. 841)
mit identischen zeitabhängigen Amplituden c für alle Atome, wodurch "cooperative atomic radiation" [MaWo] entsteht. Die Bedingung dafür ist eine "geeignete Ansammlung" (s.o.), d.h., die Ausdehnung der Ansammlung der Atome muss wesentlich kleiner sein als die Wellenlänge der Strahlung, die dann natürlich kohärent ist, wenn alle Atome in Phase schwingen. Man bildet mit den "Leiteroperatoren" b ([MaWo] S. 744, (15.2-14)):
den Erwartungswert ([MaWo] S.842, (16.6-10))
was wegen b+b = |2><2| bedeutet, dass für m=n (also in einem einzelnen Atom) paradoxer Weise keine Übergänge stattfinden. Bleibt zu erwähnen, dass in [MaWo] auf den Seiten 845-847 für N ≫ 1 eine Näherungslösung erarbeitet wird, die mit dem neoklassischen Ergebnis identisch ist. Ergänzungen 1. Dipolmatrixelement: Die Proportionalitätskonstante k (in der logistischen Gleichung, oder im Exponenten der Exponentialfunktion) ist sowohl quantenmechanisch als auch klassisch proportional zum Quadrat des Dipolmoments D und zur dritten Potenz der Frequenz f der Strahlung: k ~ D2f3. Nachfolgend das Quadrat des quantenmechanisch berechneten Dipolmoments in atomaren Einheiten für die Übergänge (n+1) → n mit jeweils maximalem Drehimpuls (l = n-1) und m = 0:
2. Weshalb diese Anführungszeichen? © März 2022, Dr. Michael Komma (VGWORT) Literatur: [MaWo] Optical Coherence and Quantum Optics, L.Mandel and E.Wolf (Cambridge University Press 1995, reprinted 2008). Links: Spontane Emission | Kaskade | Photogalerie | Photonenemission | Weisskopf-Wigner | Ensemble-Individuum | Minev Quantum Jump Moderne Physik mit MapleHOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top |

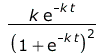 =
=
![Typesetting:-mprintslash([strahlung := `+`(`-`(`/`(`*`(`^`(N, 2), `*`(k, `*`(exp(`*`(k, `*`(N, `*`(`+`(t, `-`(t0))))))))), `*`(`^`(`+`(1, exp(`*`(k, `*`(N, `*`(`+`(t, `-`(t0))))))), 2)))))], [`+`(`-`(...](images/superrad_14.gif)