




Emission zweier Photonen
ohne Quantensprung!
Zur Legende der Animationen, siehe die Hauptseite "Emission eines Photons" und Galerie
Z-Dipol (linear polarisierte Photonen)
In den folgenden Animationen sind Übergänge von n3 = n2 +1 und n2 = n1 +1 nach n1
dargestellt und als n3 -> n2 -> n1 notiert (über den Animationen).
Für ein Dipolmoment in z-Richtung gilt m1 = m2 = m3 = 0.
Minimale Drehimpulsquantenzahlen: l3 = 2, l2 = 1, l1 = 0.
3 -> 2 -> 1 |
4 -> 3 -> 2 |
7 -> 6 -> 5 |
12 -> 11 -> 10 |
Das Elektron springt also nicht (rein zufällig) vom höheren Zustand in den niedrigeren, und überlegt sich dort eine Weile, ob es weiterspringen soll. Vielmehr kann das Atom auf (mindestens) zwei Frequenzen senden, wobei sich die Frequenz von Übergang zu Übergang erhöht, bis das Atom im Grundzustand angekommen ist. (Die Animationen zeigen nur zwei Übergänge, weil der jeweils tiefste Zustand künstlich als "Grundzustand" deklariert wurde ("Zerfallsrate" = 0)). Die Modellierung atomarer Übergänge mit Hilfe der zeitabhängigen Schrödingergleichung liefert also das genaue Gegenteil des Bohrschen Atommodells: Das Atom strahlt kontinuierlich Energie ab, allerdings auf diskreten Frequenzen. Das Problem des "in den Kern stürzenden Elektrons" entsteht nur, wenn man sich das Elektron als punktförmiges Teilchen vorstellt, das sich auf einer klassischen Bahn bewegt. Aber das Elektron ist kein punktförmiges (klassisches) Teilchen, sondern wird besser durch eine Ladungsverteilung beschrieben, die im Potential des Kerns nur "bestimmte Muster" annehmen kann. Unter diesen Mustern sind die "stationären Zustände" nicht stabile Zustände, in denen das Elektron auf Ewigkeit gefangen ist, sondern nur Muster, die sich ohne Berücksichtigung der Zeit (oder Dynamik) leicht berechnen lassen. Die Dynamik entsteht in der wellenmechanischen Beschreibung durch die Überlagerung von Zuständen, die zu Schwebungen führen.
Maximales l: l3 = n3-1 (= n2), l2 = l3 -1, l1 = l2-1 (weiterhin m1 = m2 = m3 = 0)
3 -> 2 -> 1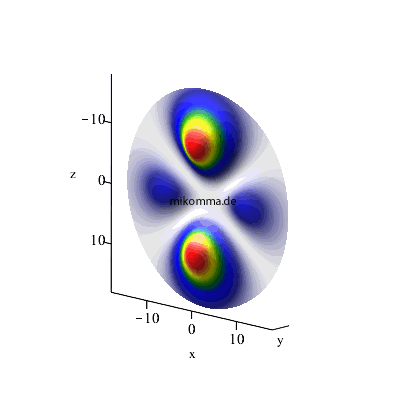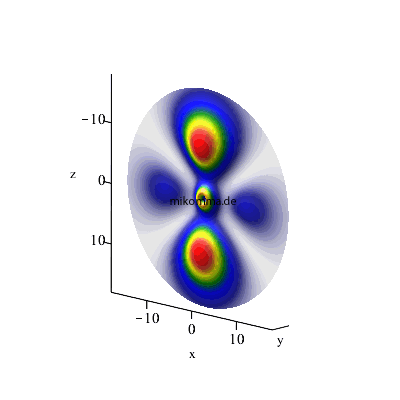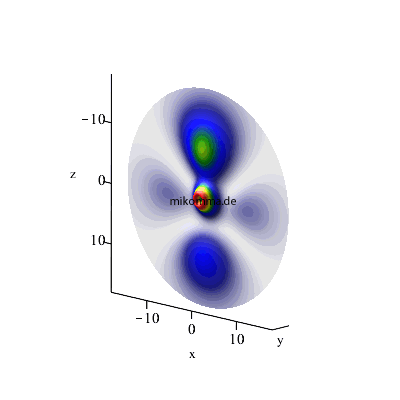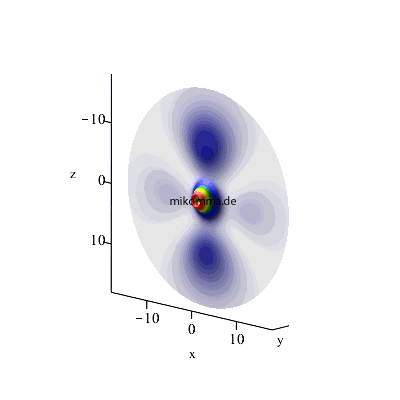 |
4 -> 3 -> 2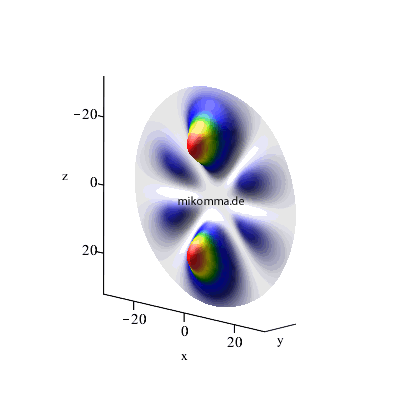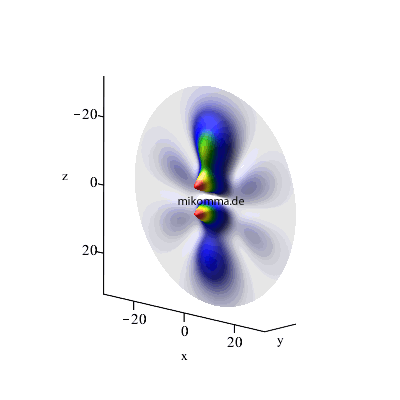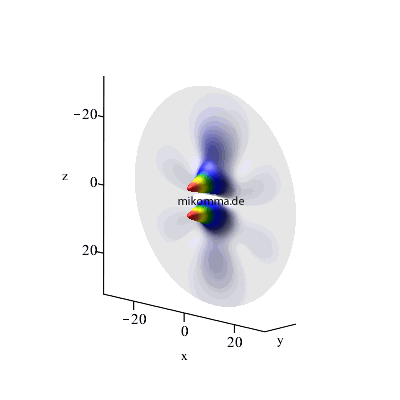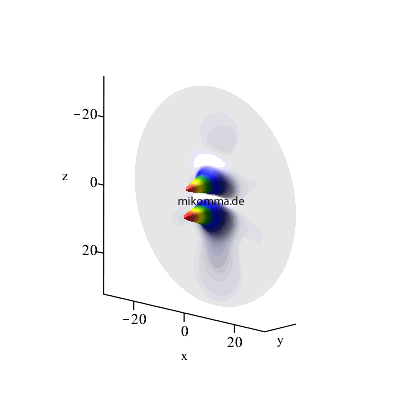 |
7 -> 6 -> 5 |
12 -> 11 -> 10 |
X-Y-Dipol (zirkular polarisierte Photonen):
So "spiralt" sich ein Elektron von einem hochangeregten "kreisförmigen Rydbergzustand" (n = 42) in den Grundzustand (n = 1).
42 -> 41 -> 40 |
22 -> 21 -> 20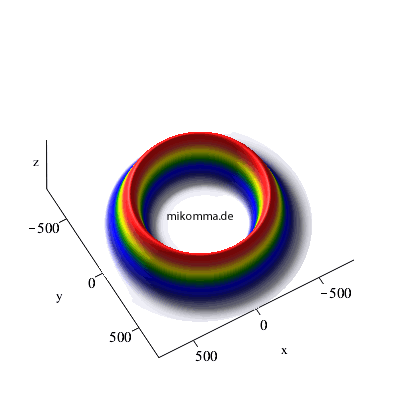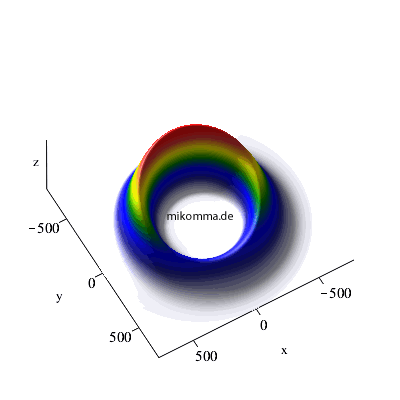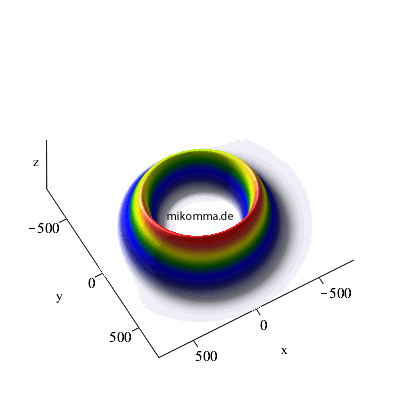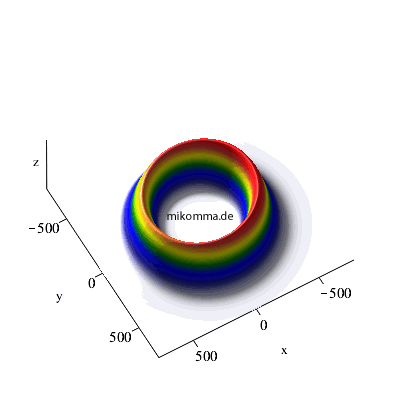 |
12 -> 11 -> 10 |
7 -> 6 -> 5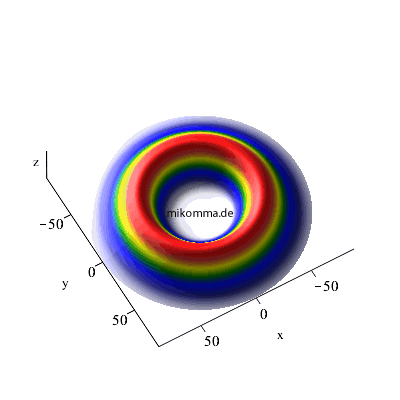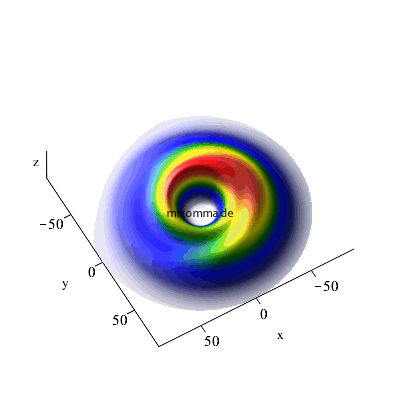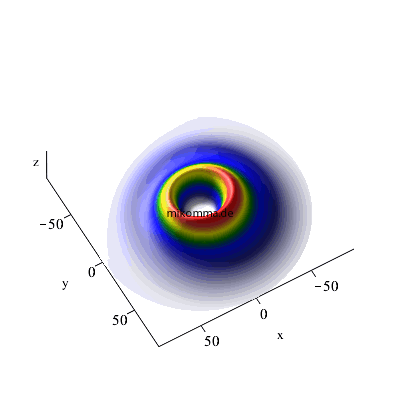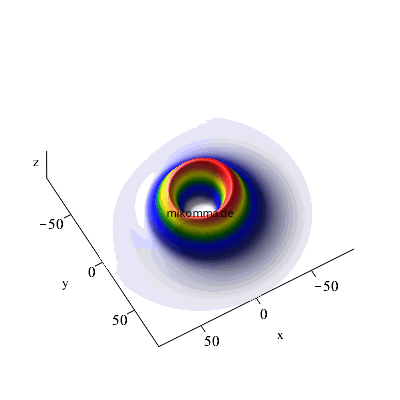 |
4 -> 3 -> 2 |
3 -> 2 -> 1 |
| Methode: Wenn man annimmt, dass Atome (auch einzelne - und nicht nur ein Ensemble :-) sich bei der Emission von Photonen an das "Gesetz des radioaktiven Zerfalls" halten (Weisskopf-Wigner-Näherung), dann gilt für die "Zerfallsreihe" A -> B -> C mit den "Zerfallskonstanten" ka und kb (kc = 0), bzw. für die Besetzungszahlen von A, B und C: |
 |
| Berechnet man mit diesem Ansatz wie in "Emission eines Photons" die emittierte Strahlung, so ergibt sich z.B. folgendes Bild: |
 |
| Legende: - nicht oszillierende Kurven: Der Zustand A (Mutter) zerfällt exponentiell, der Zustand B (Tochter) wird vorübergehend besetzt und der Zustand C (Enkelin) nähert sich 1 (der Summe der Besetzungszahlen), weil als stabil vorausgesetzt. Die fünfte nicht oszillierende Kurve ist eine Einhüllende: - oszillierende Kurven: A -> B: kleine Frequenz, schnell abklingend (große "Zerfallsrate"), B -> C: große Frequenz, erst zunehmend, dann langsam abklingend (mit Einhüllender oben), A -> B -> C: Resultierende Strahlung der Kaskade, zur besseren Sichtbarkeit um 2 nach oben versetzt. |
© Mai 2017, Dr. Michael Komma (VGWORT)
Siehe auch:
Galerie | Emission eines Photons | Spontane Emission, logistisch | Weisskopf-Wigner | Ensemble-Individuum
Historisches zum Quantensprung
H-Orbitals aus ' Moderne Physik mit Maple'
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top